Введение 1 Наука о сопротивлении материалов

• Название: Введение 1 Наука о сопротивлении материалов
• Дата: 24.08.2022
• Размер: 4.19 Mb.
• Имя файла: konspektlekciisoprotivleniematerialov.doc
• Тип: Лекция; #651978
• страница: 10 из 12

4.6 Главные оси и главные моменты инерции сечения

Главными называются центральные оси, относительно которых осевые моменты инерции сечения достигают экстремальных значений, а центробежный момент инерции равен нулю.

Сформулированному положению отвечает система осей, проходящих через центр тяжести сечения, если хотя бы одна из них является осью симметрии.

Определение моментов инерции сложного составного сечения относительно главных осей

Пример 1

Определить положение главных осей и величины главных моментов инерции сечения прямоугольной формы с отверстием, центр тяжести которого находится на расстоянии 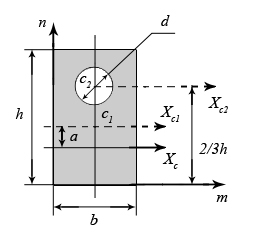от основания прямоугольника, при . рис.4.11)




Определяем положение центра тяжести сечения. В силу симметрии координата 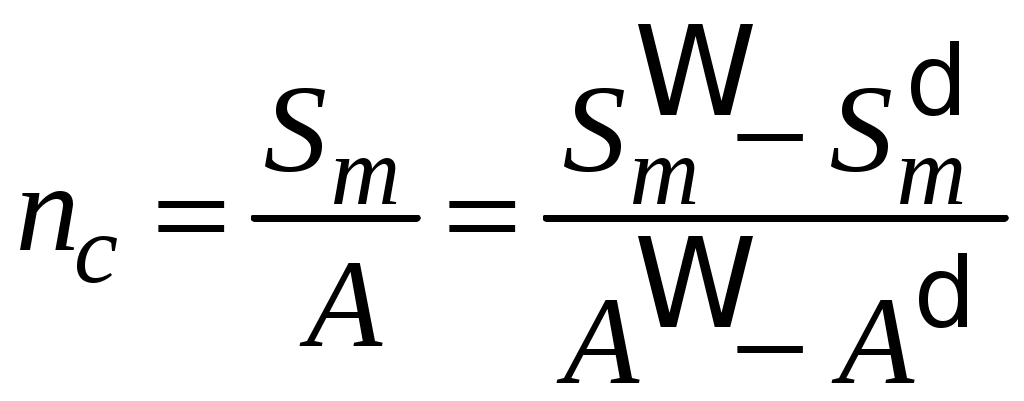(в осях mn). Координата может быть определена с использованием понятия статического момента площади относительно оси m , отсюда

(4.16)

Рис 4.11

Здесь ;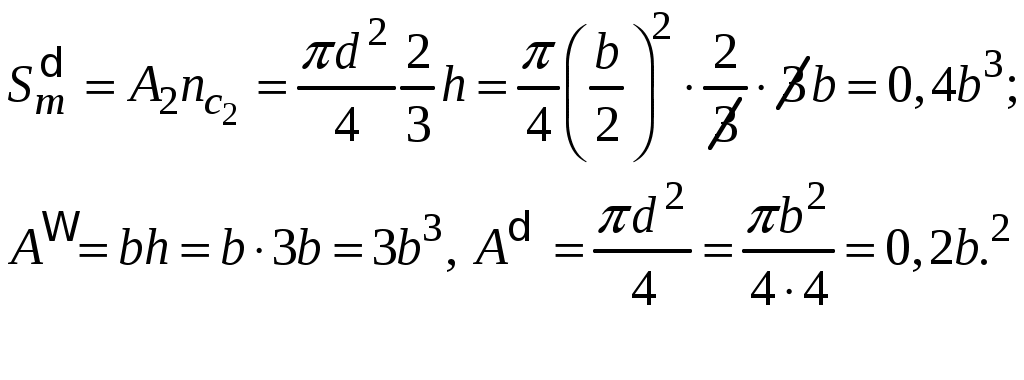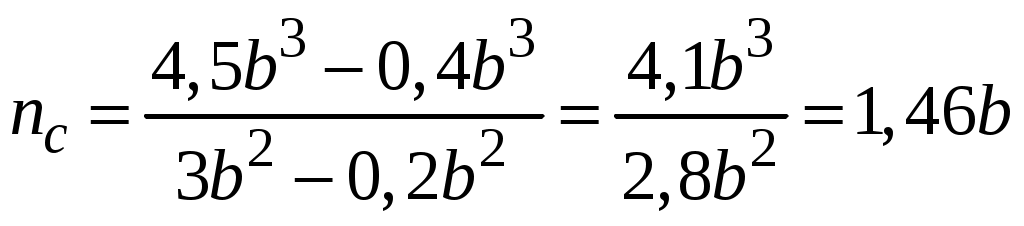





Расстояние между осями и обозначим.

Расстояние между осями и обозначим .



На основании (4.8) . Для оп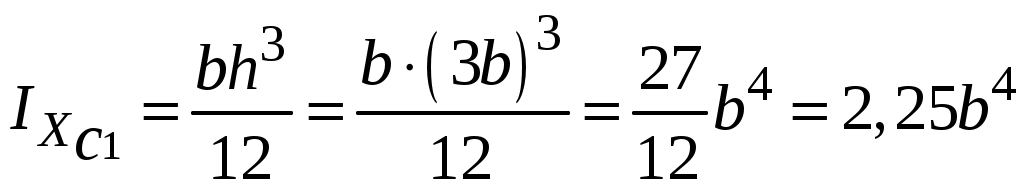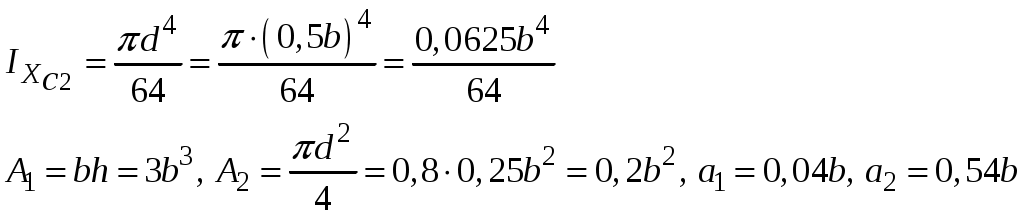ределения главного момента инерции сечения необходимо воспользоваться теоремой о параллельном переносе осей, в соответствии с которой



Здесь

.

Ось 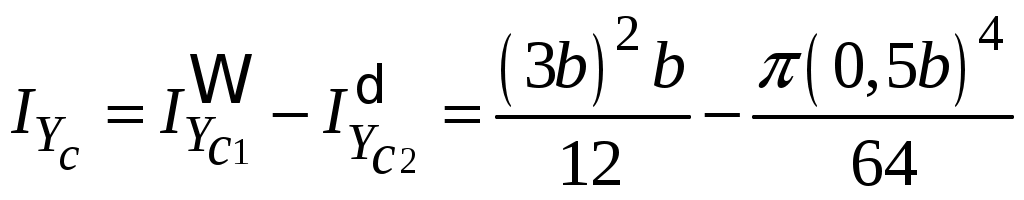− главная центральная ось сечения совпадает с главными центральными осями составляющих сечения .

.

Геометрические характеристики стандартных прокатных профилей: двутавр , швеллер , уголки равнобокие и неравнобокие приводятся в технических справочниках, а также (выборки из ГОСТа) приведёны в учебниках по сопротивлению материалов.

Лекция 5

5. Кручение
Кручение – такой вид нагружения стержня, при котором из шести внутренних силовых факторов в поперечном сечении стержня действует только один – крутящий момент.

Рассмотрим круглый стержень, называемый валом. Нанесем на поверхность вала сетку взаимно-ортогональных линий, (рис.5.1,а). После деформации кручения происходит смещение (сдвиг) линий, идущих вдоль оси стержня, а расстояния между поперечными сечениями остаются неизменными (рис.%.1 б).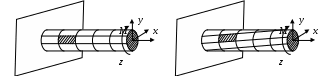


(а) б)
Рис. 5.1
Поверхностные прямоугольники после деформации кручения преобразуются в параллелограммы. Считаем, что внутри вала деформация происходит аналогичным образом.

Основные гипотезы. Поперечные сечения при кручении остаются плоскими, расстояния между сечениями остаются неизменными. Это – гипотеза плоских сечений. Брус, подвергаемый кручению, состоит из множества плоских тонких дисков, нанизанных на ось. Каждый диск равномерно поворачивается по отношению к смежным, при этом оставаясь плоским. Ось бруса сохраняет первоначальную длину.

Из допущений следует, что кручение бруса состоит из взаимного сдвига поперечных сечений, следовательно, в поперечных сечениях возникают только сдвиговые (касательные) напряжения.
Распределение касательных напряжений при кручении
Рассмотрим консольный брус круглого поперечного сечения, нагруженный парой сил с моментом m, плоскость действия которого ортогональна оси бруса (рис.5.2, а). Применяя метод сечений, устанавливаем, что в поперечных сечениях бруса возникает только крутящий момент ( рис.5.2 б).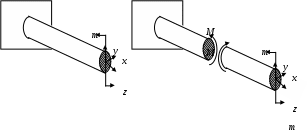

(а) (б)


Выделим элемент бруса длиной dz, рис. 5.1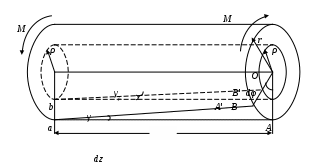



Рис. 5.1


Пусть радиус вала равен r. Выделим внутри вала цилиндр с радиусом основания ρ < r и рассмотрим деформации образующей наружного цилиндра aA и внутреннего – bB. При кручении aA повернется на угол γ и займет положение aA', bB займет положение bB', повернувшись на угол γ_ρ. Выразим углы поворота γ, γ_ρ через угол закрутки поперечного сечения dφ. Имеем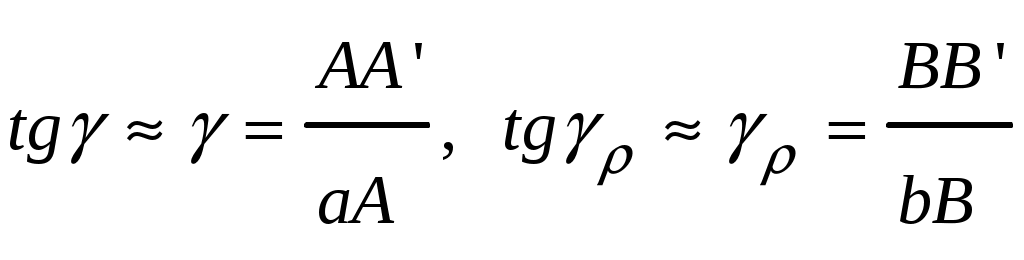

.

С другой стороны, из геометрии поперечного сечения для дугAA' и BB' выполняется

.

С учетом того, что aA = bB = dz, получаем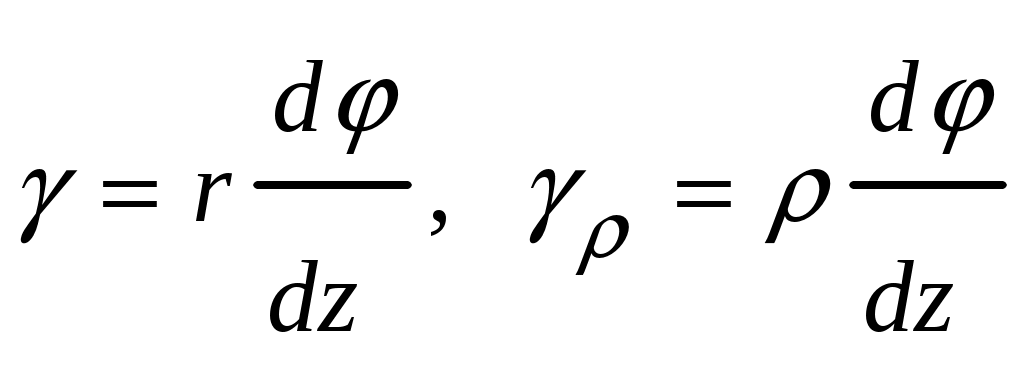

.

Так как кручение бруса есть взаимный сдвиг поперечных сечений, то, согласно закону Гука, при сдвиге касательное напряжение τ выразится через γ следующим образом: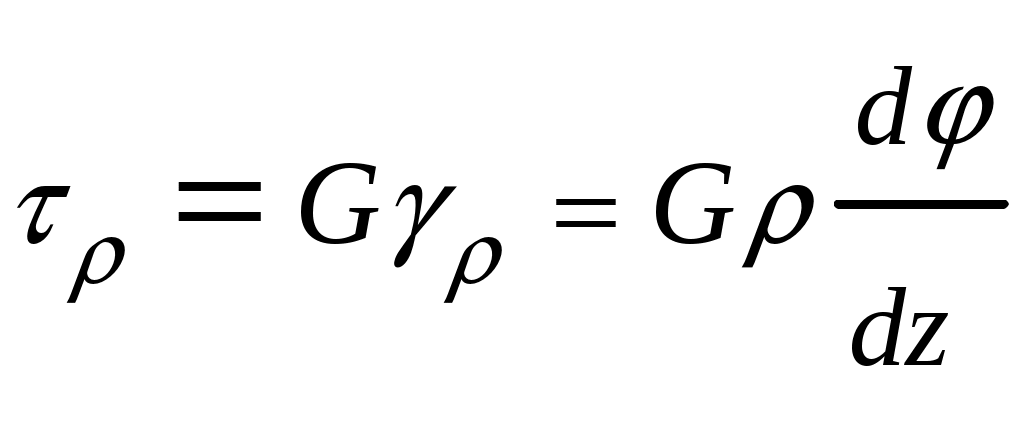

. (5.1)

При ρ = 0 τ_ρ = 0, при ρ = ρ_max = r имеем τ_ρ = τ_max.

Т 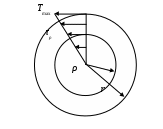аким образом, касательное напряжение пропорционально расстоянию по радиусу от центра поперечного сечения вала и достигает максимального значения на его внешней поверхности. Распределение напряжений можно представить треугольной эпюрой, рис. 5.2.


Рис. 5.2

Связь между касательным напряжением

и внутренним крутящим моментом
Н 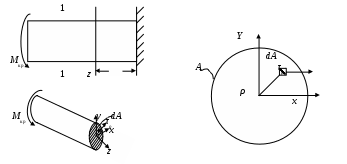айдем связь между касательным напряжением τ и крутящим моментом. Для этого воспользуемся методом сечений, рис. 5.3. Рассмотрим поперечное сечение вала на расстоянии z от заделки.

Рис. 5.3
Рассмотрим равновесие отсеченной части. На элементарной площадке dA на расстоянии ρ от центра действует сдвиговое (касательное) напряжение τ_ρ. Элементарная сила, действующая на площадке dA

.

Элементарный момент силы dQ относительно оси z

.

Суммарный момент, собираемый с площади A, будет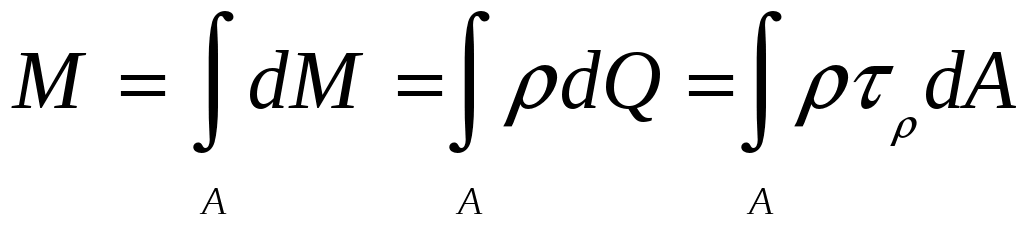

.

Подставляя сюда выражение τ_ρ из (5.1), получим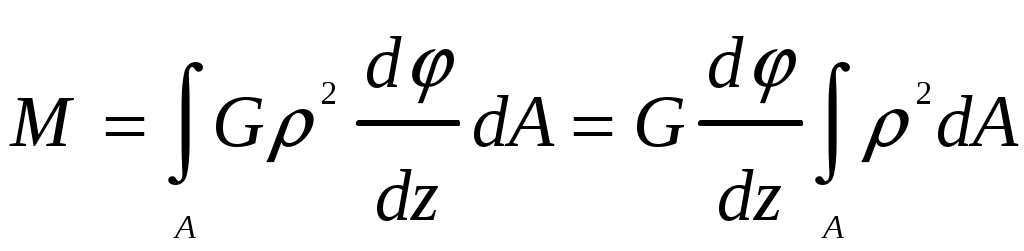

.

Здесь 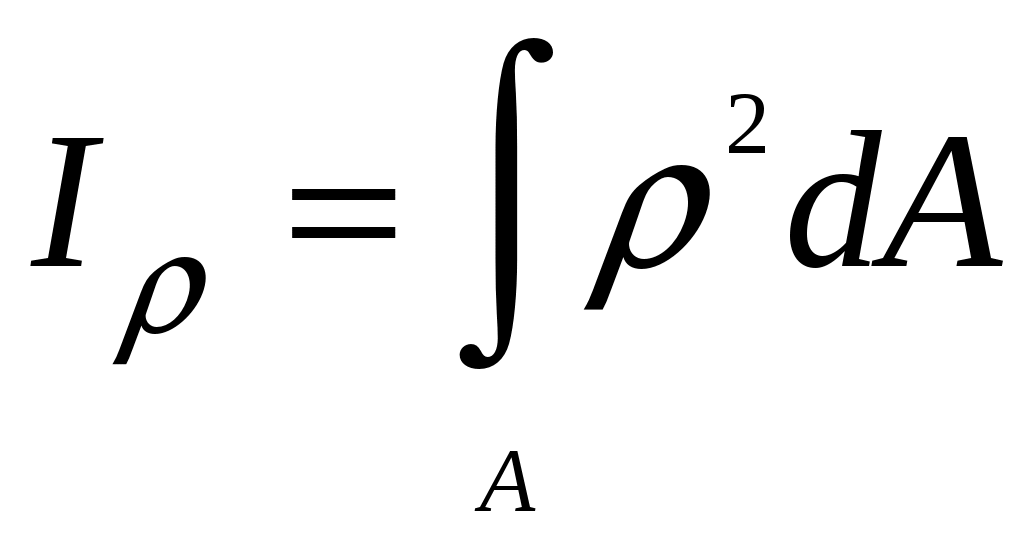- полярный момент инерции сечения. Значит

.

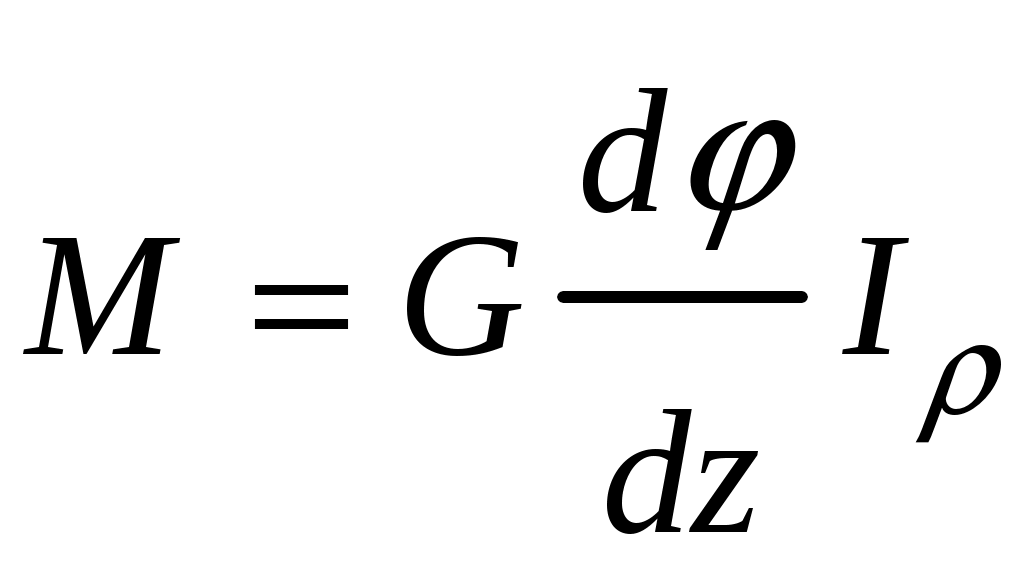Из условия равновесия отсеченной части M = M_кр. Следовательно,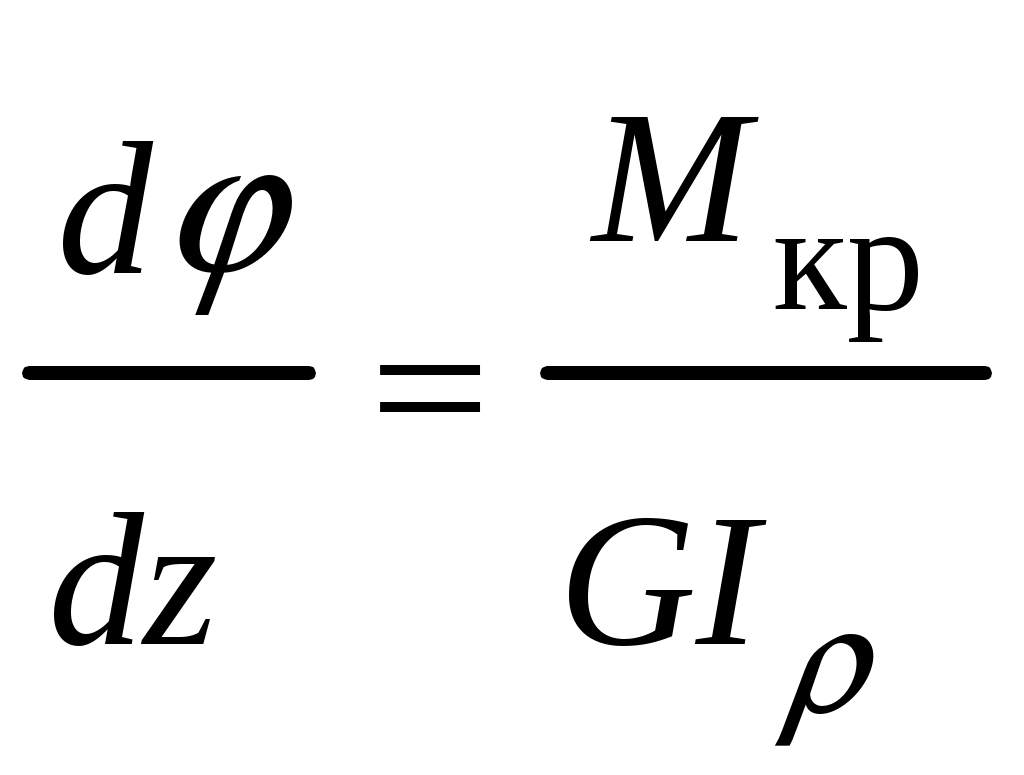

. (5.2)

Из закона Гука при сдвиге (5.1) имеем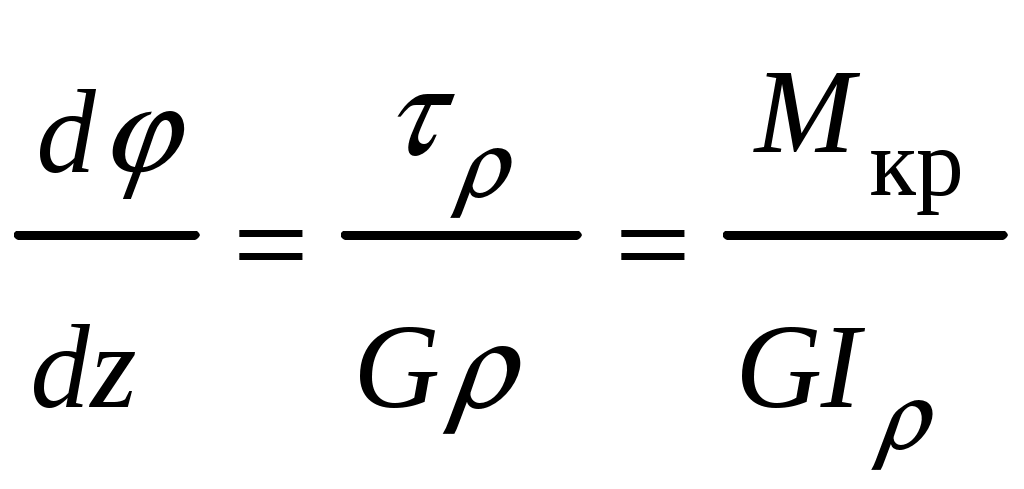

.

Отсюда получаем искомое соотношение между касательным напряжением и крутящим моментом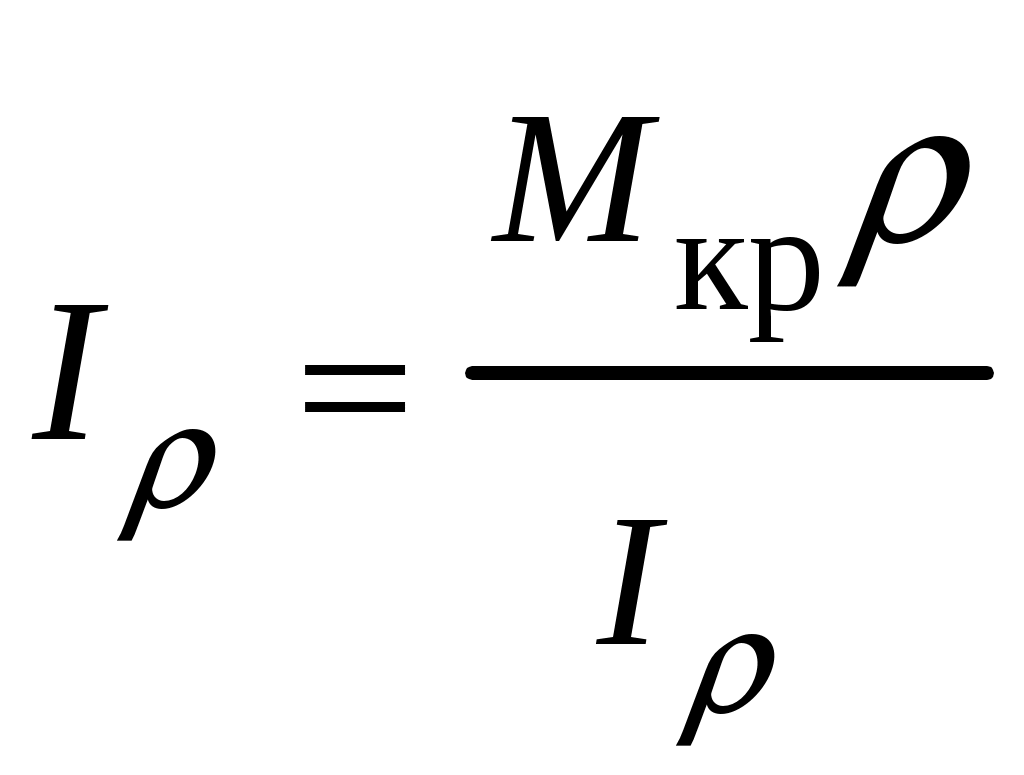

. (5.3)

Максимальное значение касательного напряжения по радиусу вала будет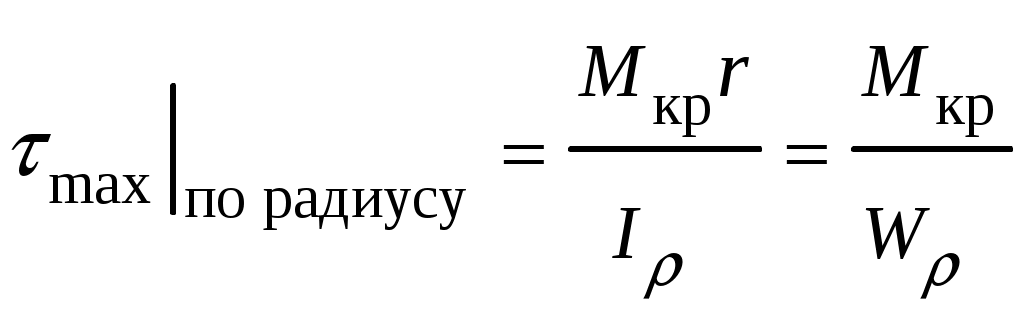

. (5.4)

Здесь W_ρ – полярный момент сопротивления

.

Д 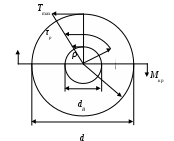ля кольцевого сечения


полярный момент сопротивления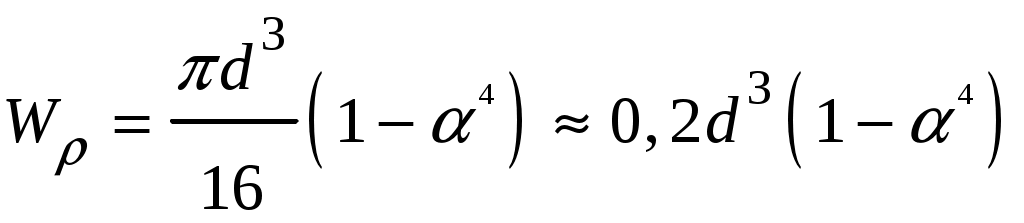

,

где 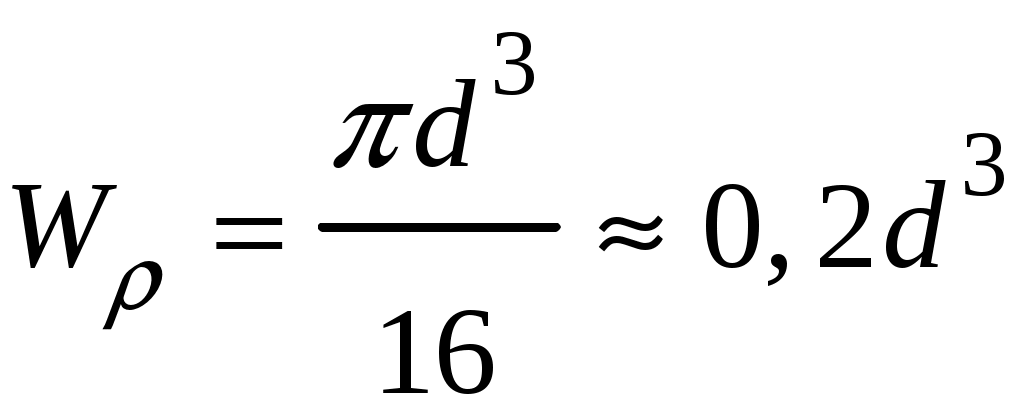. Для круглого сечения и получаем

.
Условие прочности при кручении
Данное условие имеет вид:

.

Здесь 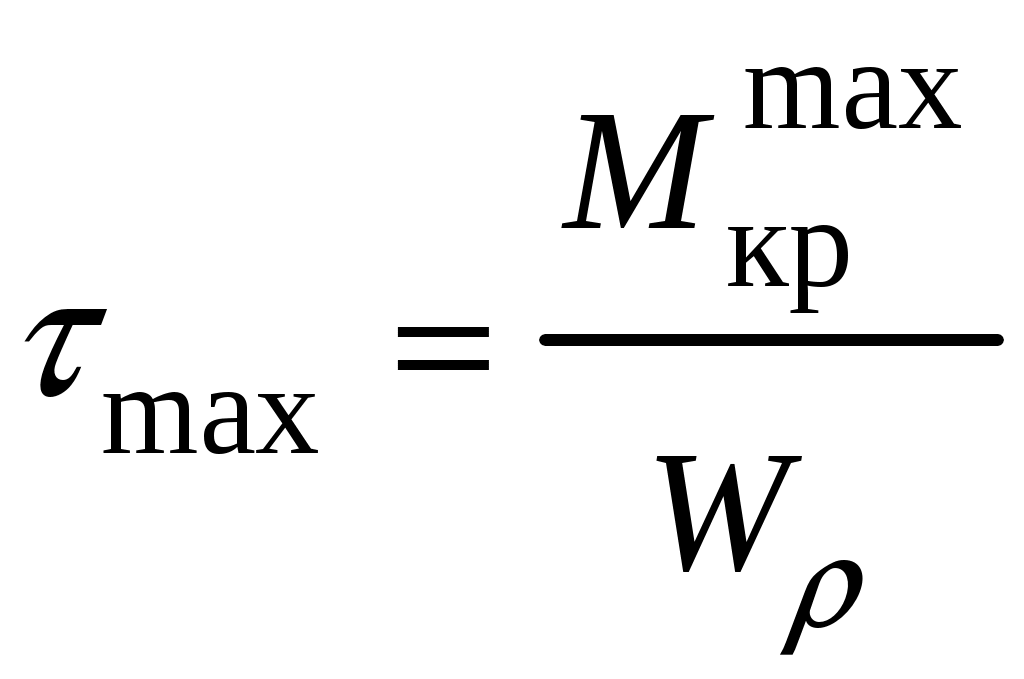- допускаемое касательное напряжение, которое при действии статической нагрузки принимают равным , - наибольшее значение касательного напряжения в скручиваемом брусе, которое выбирается максимальным по двум измерениям: по радиусу вала и его длине. Если диаметр вала постоянен по длине, то согласно (5.4)

.

Если же имеем вал с кусочно-постоянным сечением по длине, то 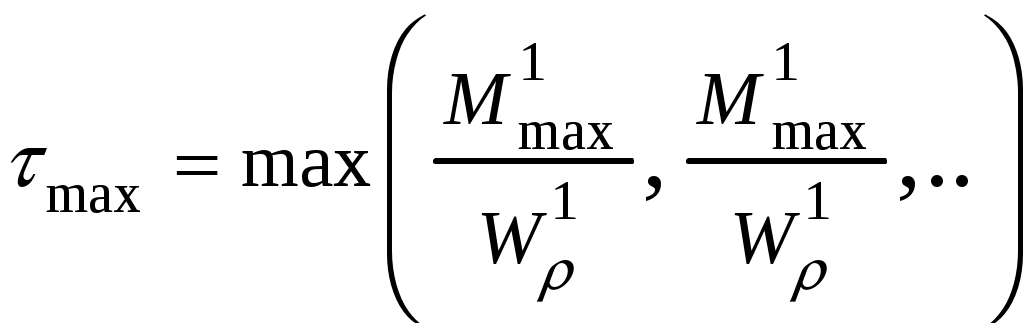рассчитывается по формуле

,

где - максимальные значения крутящих моментов в пределах каждого участка, имеющего постоянный диаметр, - соответствующие моменты сопротивления.
Построение эпюр угловых перемещений при кручении
Если крутящий момент и диаметр сечения вала зависят от продольной координаты z, то согласно (5.2) угол закручивания рассматриваемого сечения относительно неподвижного будет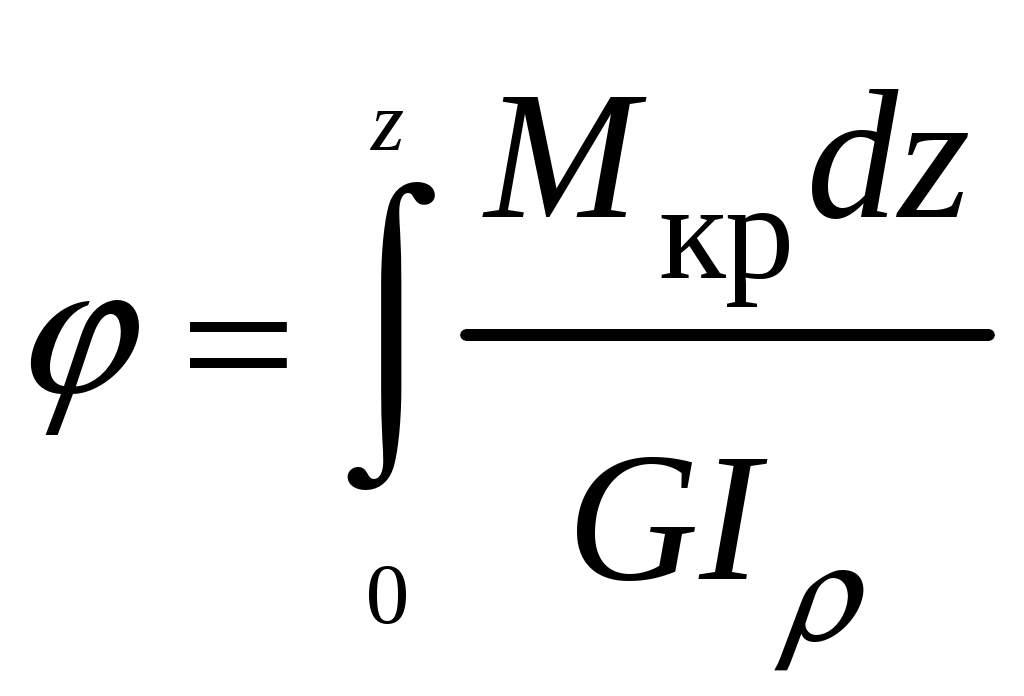

. (5.5)

Произведение называют жесткостью сечения при кручении

В случае, если крутящий момент в сечении постоянен, а диаметр сечения не меняется на длине AB,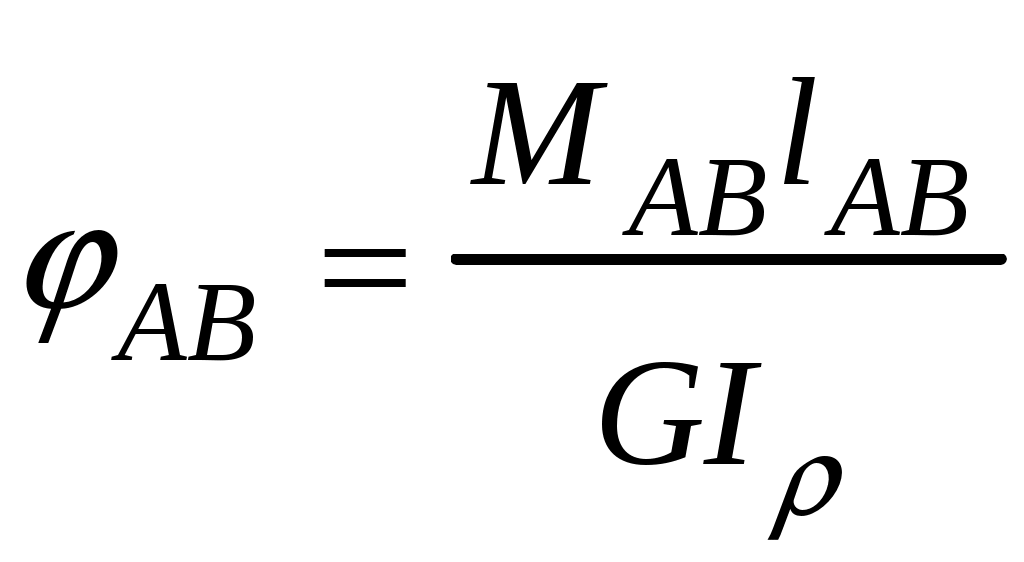

,

где 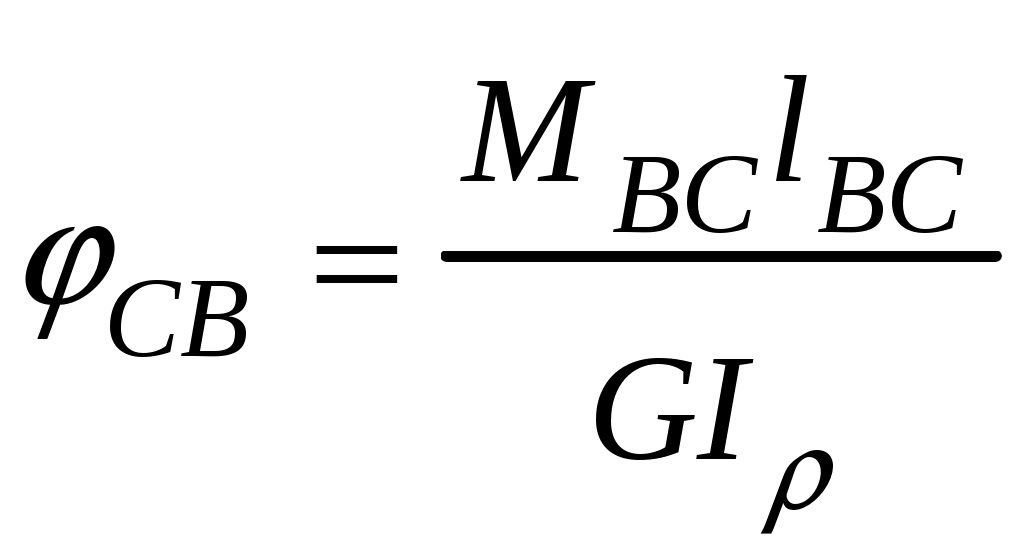- крутящий момент на участке AB, - длина участка AB. Угол закручивания в сечении С относительно сечения B будет

.

Так как сечение B не является неподвижным, то угол закрутки сечения С относительно сечения A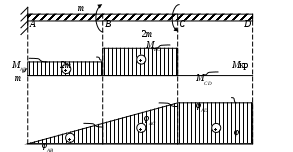

.

Рис. 5.4

Пример расчета эпюры крутящих моментов M_кр и углов закрутки φ приведен на рис. 5.4.
Условие жесткости при кручении
Введем угол закручивания стержня, приходящийся на единицу длины (погонный угол закрутки)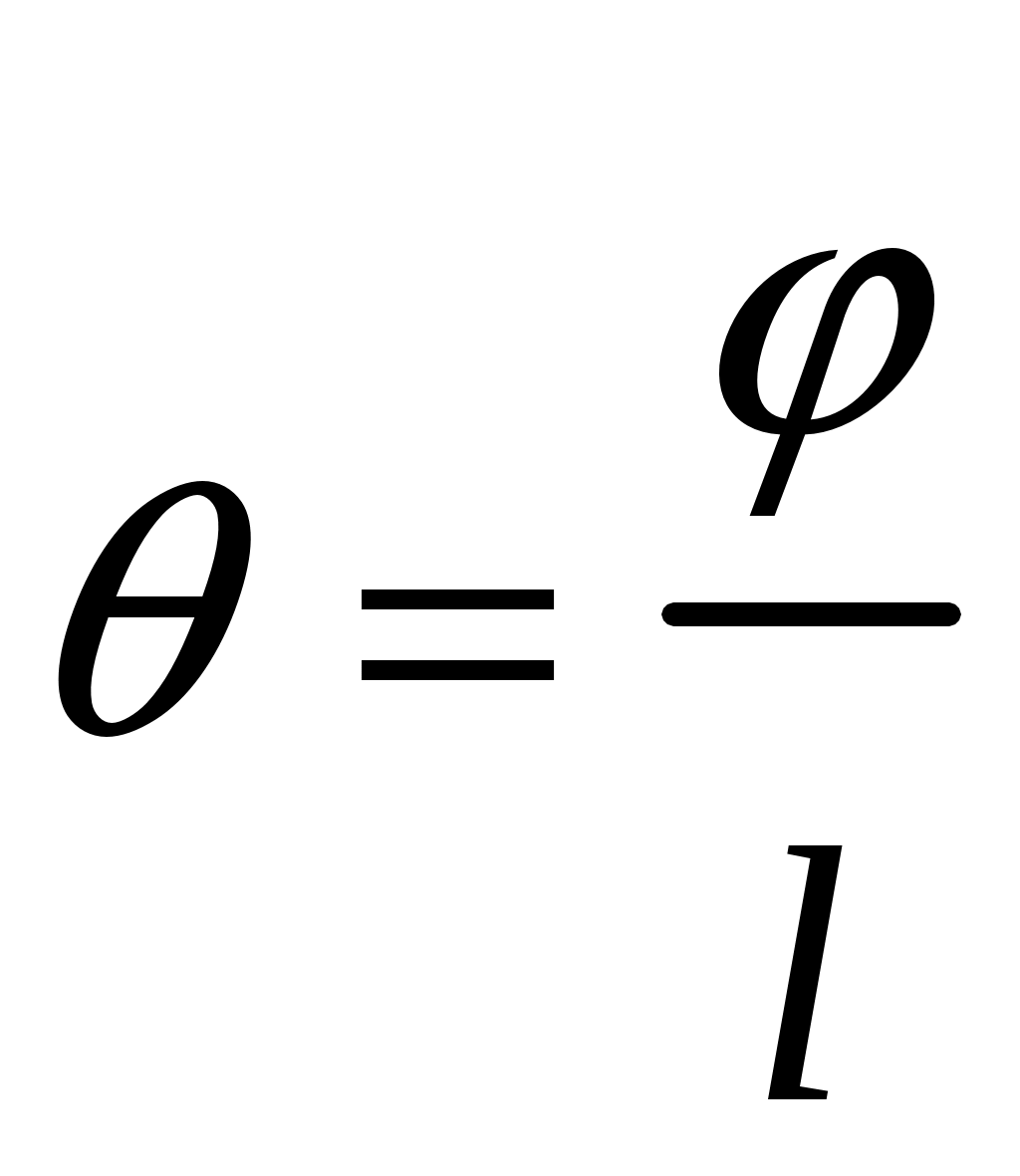

.

Условие жесткости при кручении приводит к ограничению на величину погонного угла закрутки

,

где - наиболь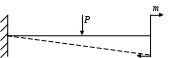шее значение погонного угла закрутки, - предельно допускаемое значение .

6. Изгиб
И згибом называется деформация бруса, возникающая под действием нагрузок, ортогональных оси, или пары сил, действующих в плоскостях, содержащих продольную ось стержня.

Стержень, работающий на изгиб, называется балкой.

Выделяют плоский (или поперечный) и косой изгибы.

Плоский изгиб, рис. (а) – такая деформация бруса, при которой плоскость действия внешних сил проходит через одну из главных центральных осей инерции сечения (или осей симметрии). При плоском изгибе деформация идет в плоскости действия силы.

К 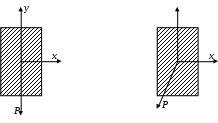осой изгиб, рис. (б) – такая деформация, при которой плоскость действия внешних сил не содержит ни одну из главных центральных осей инерции (осей симметрии).


(а) (б)
Классификация нагрузок, производящих изгиб
1. Сосредоточенная сила. Считается, что площадь приложения данной нагрузки мала по сравнению с длиной балки, поэтому принимается, что сила приложена в точке, рис. (а)

2. Сосредоточенный момент – пара сил, приложенных в точке, рис. (б)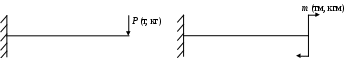



(а) (б)
3. Распределенная нагрузка:

• 
  равномерно-распределенная нагрузка, интенсивность нагрузки по длине q (погонная нагрузка) постоянна, рис. (в);
  
• 
  неравномерно-распределенная нагрузка – в этом случае интенсивность нагрузки по длине q≠ const, рис. (г, д).
  

(в) (г) (д)
Понятие об изгибающем моменте и перерезывающей силе
Внешние нагрузки, действующие на балку, вызывают появление внутренних усилий. При любом расчете на прочность и жесткость необходимо знать характер их распределения по длине и толщине балки.

Рассмотрим сечение I-I на расстоянии z₁ от левого конца балки



Действие внешних нагрузок вызывает появление в сечении уравновешивающей силы Q и изгибающего момента M.

Поперечная (перерезывающая) сила Q равна алгебраической сумме всех внешних сил, расположенных по одну сторону от рассматриваемого сечения.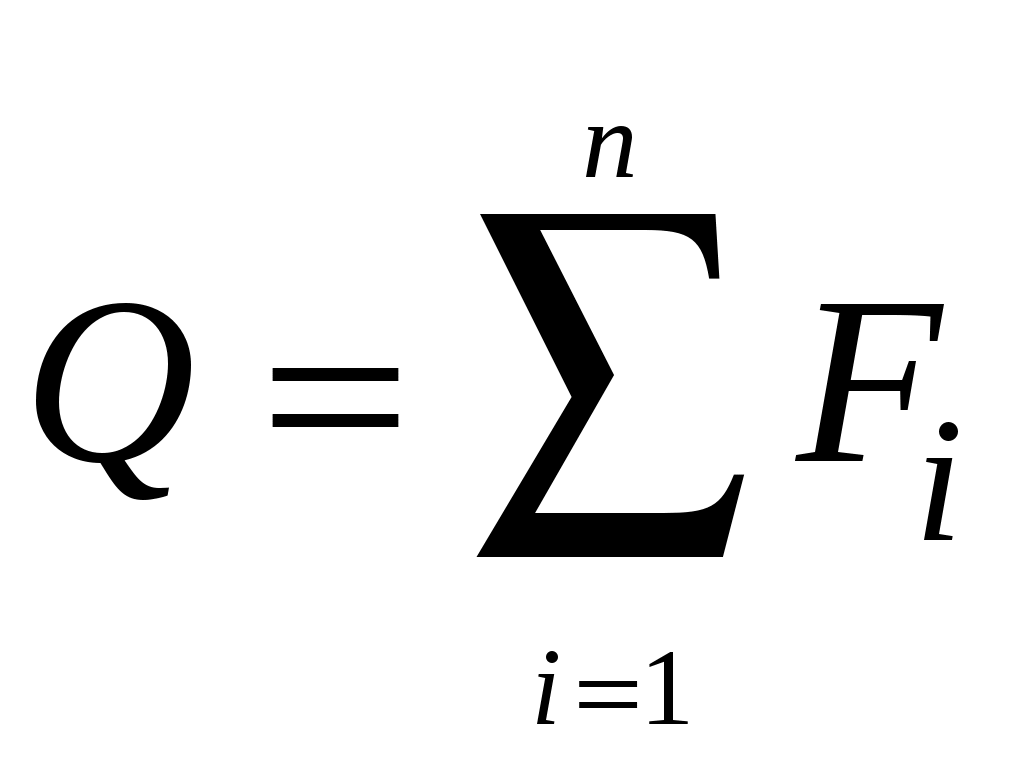



Изгибающий момент в точке рассматриваемого сечения относительно оси, проходящей через центр тяжести сечения и ортогональной плоскости действия нагрузки, равен алгебраической сумме моментов всех внешних нагрузок, приложенных по одну сторону от сечения.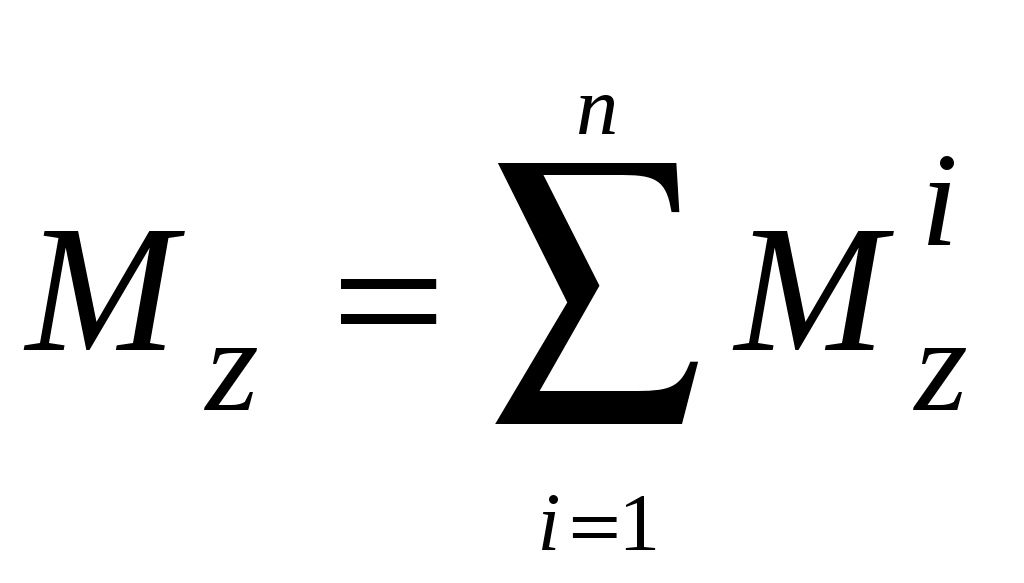


Правило знаков для Q, M
Знаки перерезывающей силы Q и изгибающего момента M зависят от того, какая часть балки рассматривается: правая или левая. Поперечная сила в сечении положительна, если равнодействующая внешних сил слева от сечения направлена снизу-вверх, справа от сечения – сверху-вниз, и отрицательная в противном случае.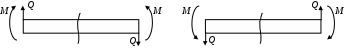


Q > 0 Q < 0

M > 0 M < 0
Изгибающий момент положителен, если равнодействующая внешних моментов изгибает балку выпуклостью вниз; изгибающий момент отрицателен, если изгиб происходит выпуклостью вверх.

M > 0 M < 0


Зависимость между изгибающим моментом, поперечной силой
и интенсивностью погонной нагрузки (теоремы Журавского)

Рассмотрим балку, нагруженную произвольной нагрузкой, рис (а).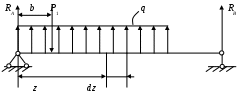




(a)

Определим поперечную силу в сечении, отстоящем от левой опоры на расстоянии z. Проецируя на вертикаль силы, расположенные левее сечения, получим

.

Аналогично для сечения z+dz имеем

.

Вычитая из второго уравнения первое, получаем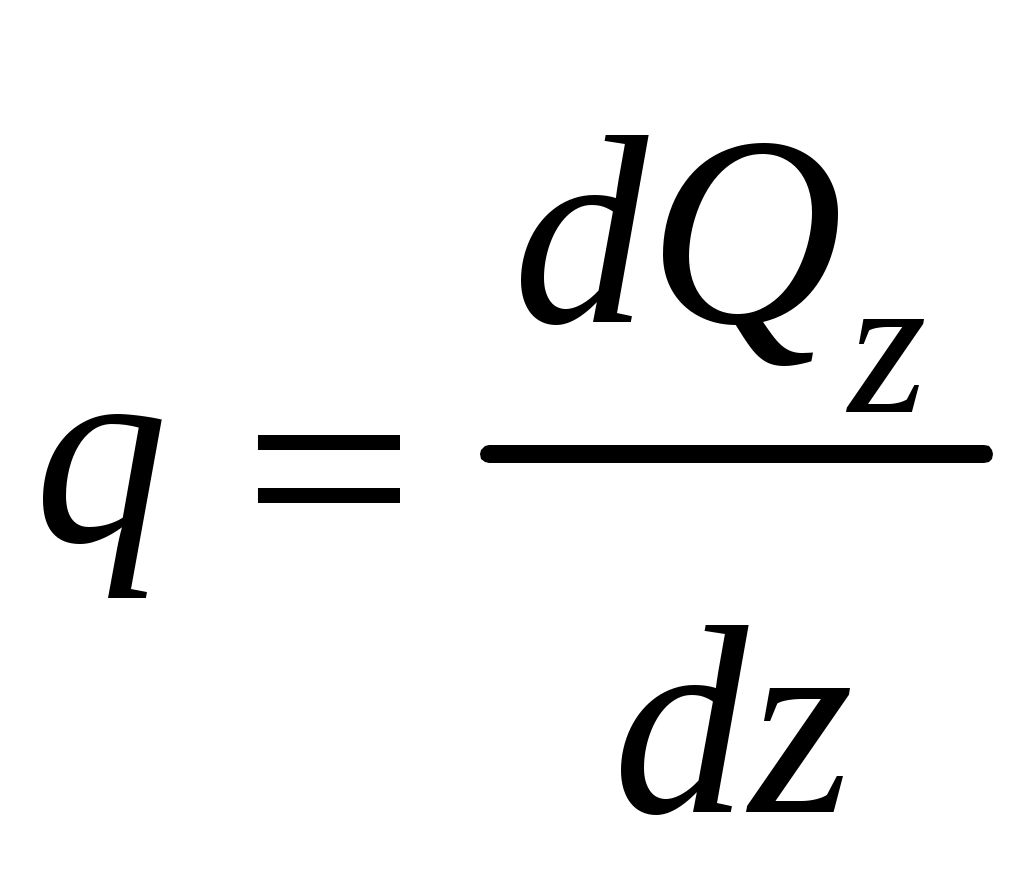

. (а)

Таким образом, производная от поперечной силы по продольной координате равна интенсивности погонной нагрузки (первая теорема Журавского).

Вычислим изгибающий момент в сечении с абсциссой z. Распределенную нагрузку на участке длиной z заменим ее равнодействующей, равной qz и приложенной к середине участка, на расстоянии z/2 от сечения.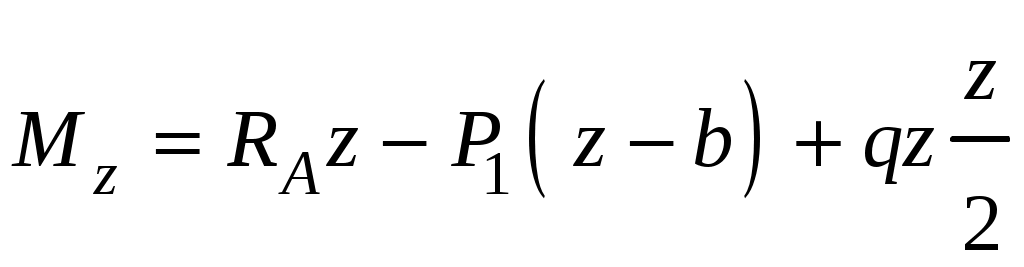

.

Изгибающий момент в сечении z+dz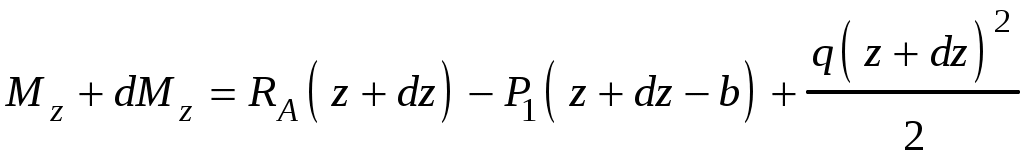

.

Разность двух последних уравнений есть (пренебрегаем слагаемым )

.

Следовательно,

. (б)

Производная от изгибающего момента по продольной координате равна поперечной силе (вторая теорема Журавского).

Из (а) и (б) следует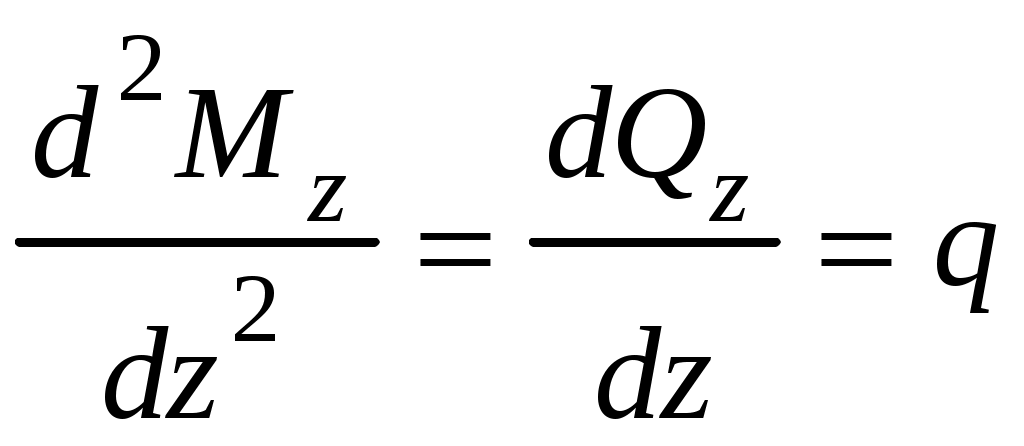

. (в)

Полученные зависимости используются при построении эпюр изгибающих моментов и поперечных сил.

Из зависимостей (а) – (в) вытекают правила, которые определяют характер эпюр Q, M и применяют для контроля правильности их расчета.

1. Если на участке отсутствует погонная нагрузка, q = 0, то эпюра Q– прямая, параллельная оси z, эпюра M – наклонная прямая.

2. На участке с равномерно распределенной нагрузкой q= const, эпюра Qпредставляет наклонную прямую, эпюра M – параболу, направленную выпуклостью навстречу q.

3. На участках, где Q > 0, изгибающий момент возрастает; если Q < 0, то изгибающий момент убывает (в случае правосторонней системы координат). Если Q = 0, то изгибающий момент постоянен.

4. Если перерезывающая сила пересекает ось z, Q = 0, то в данном сечении момент имеет максимум, если Q меняет знак с плюса на минус; минимум в противоположном случае.
Нормальные напряжения при чистом изгибе
Согласно определению чистого изгиба, поперечная сила равна нулю в каждом сечении балки, поэтому M= const (поскольку 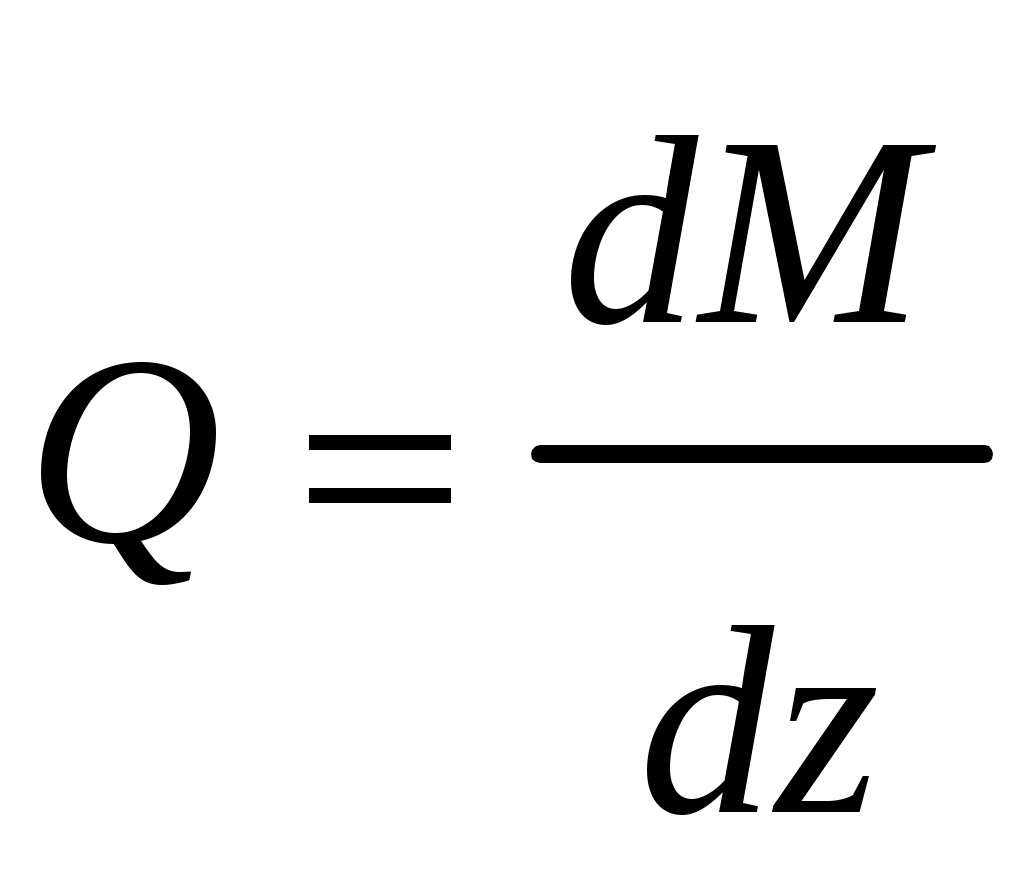). При чистом изгибе в поперечных сечениях балки возникают изгибающие моменты в плоскости, содержащей одну из главных центральных осей инерции.

Чтобы установить закон распределения внутренних сил, возникающих в поперечном сечении балки, уравнений статики недостаточно, необходимо рассмотреть геометрическую сторону задачи. Согласно гипотезе плоских сечений, поперечные сечения балки, плоские до деформации, рис. (а), остаются плоскими и после деформации, рис. (б).




(а) (б)
Деформацию изгиба можно представить как поворот сечений по дуге окружности радиусом ρ.

Рассмотрим два смежных сечения и выделим элемент длиною dz. Взаимный поворот смежных сечений на угол dθ.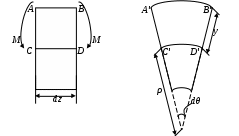


В результате изгиба верхние слои балки удлинятся, нижние – укоротятся. Существует слой CD = C'D', длина которого не изменится. Положение слоя CDпока не известно. Выразим длину CDчерез угол dθ как элемент дуги окружности

.

Отрезок AB на расстоянии y от слоя CD удлинится на

.

Относительная деформация есть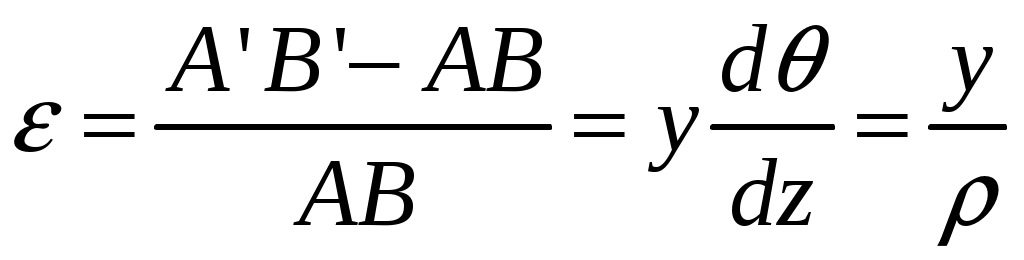

.

Если принять справедливость гипотезы ненадавливания волокон, то продольные слои балки находятся в состоянии растяжения и сжатия. Переход к напряжениям осуществляется по закону Гука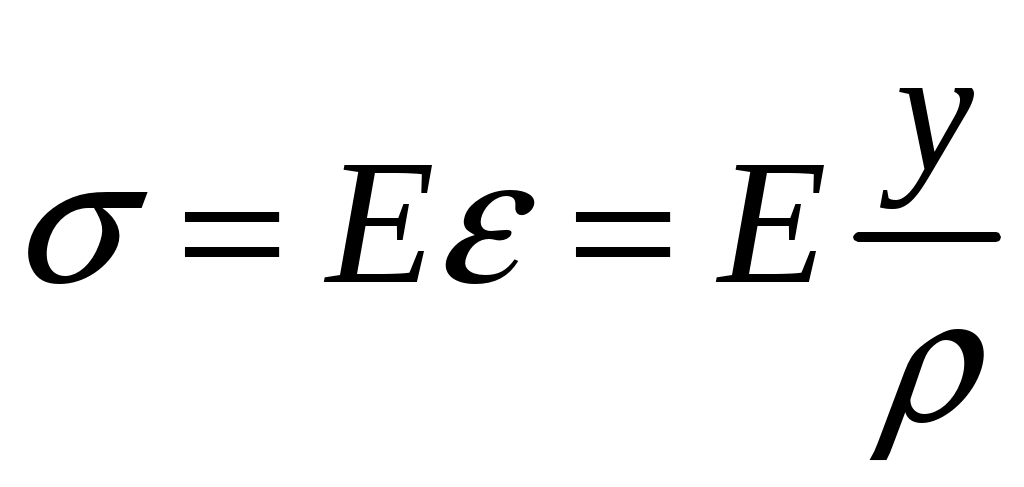

. (6.1)

Здесь ρ – радиус кривизны нейтрального слоя.

Координата y отсчитывается от нейтрального слоя (нейтральной линии): вверх от нейтральной линии y > 0, вниз – y < 0. В соответствии с этим фактом в силу того, что E > 0, ρ > 0, напряжения σ будут либо положительными (растягивающими), либо отрицательными (сжимающими).
Связь между нормальным напряжением и изгибающим моментом
Р 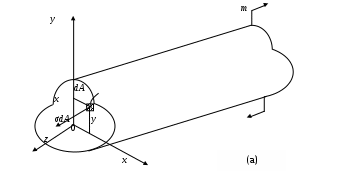ассмотрим равновесие части балки, находящейся под действием внешнего изгибающего момента m и внутренних сил, возникающих в поперечном сечении балки. Начало координат в поперечном сечении поместим на нейтральной линии, рис. (а).

Сумма элементарных нормальных сил , действующих по нормали от рассматриваемого сечения, есть интеграл по площади A:

.

Поскольку при чистом изгибе действует только момент m, продольная сила отсутствует, то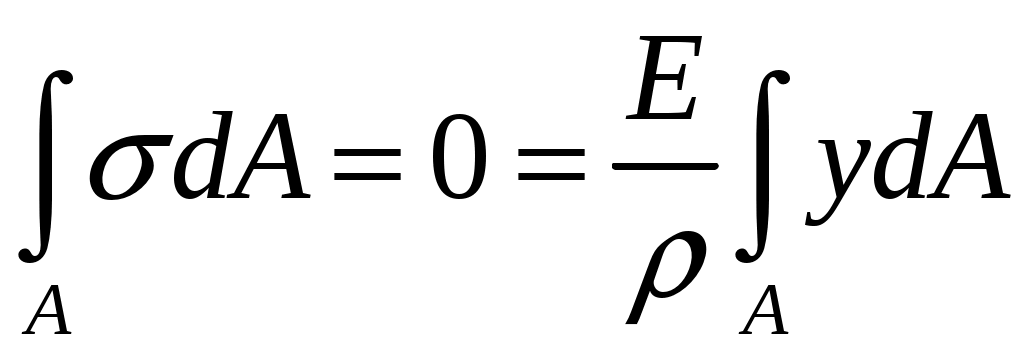

.

Последний интеграл есть статический момент площади поперечного сечения балки S_x относительно оси x, которая совпадает с нейтральной линией. Так как , то

.

Согласно теоремы Вариньона, статический момент равен нулю только в том случае, если ось координат проходит через центр тяжести поперечного сечения. Значит, положение нейтральной линии установлено: она проходит через центр тяжести поперечного сечения.

Найдем момент элементарных нормальных сил

.

Сумма моментов относительно оси х

.

На основании формулы (6.2) для нормальных напряжений получаем

.

Интеграл 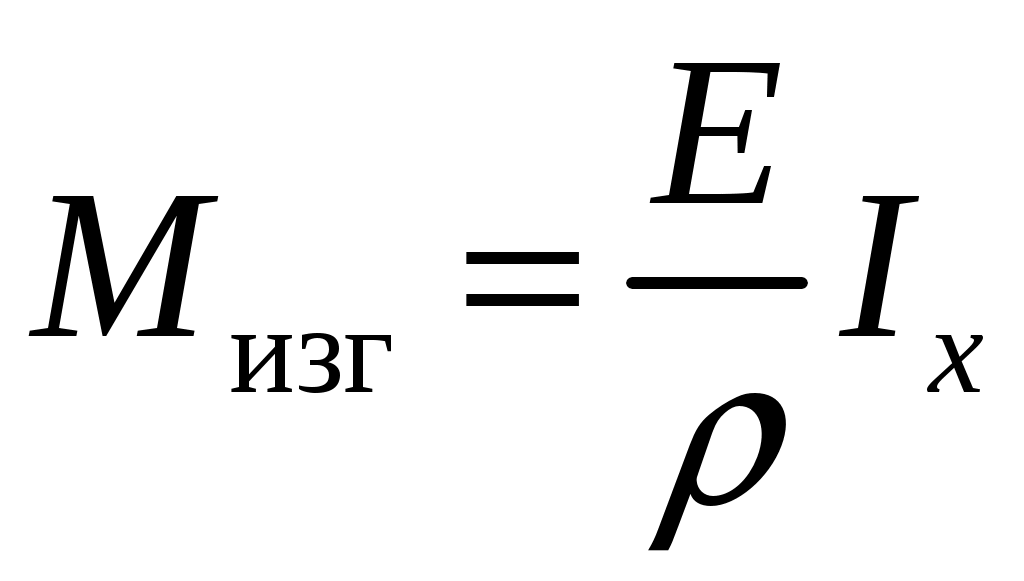представляет собой момент инерции сечения относительно оси x. На отсеченную часть балки может действовать не один момент m, а несколько. Тогда уравнение равновесия будет содержать алгебраическую сумму моментов всех внешних сил, которая равна изгибающему моменту в рассматриваемом поперечном сечении. Следовательно,

,

откуда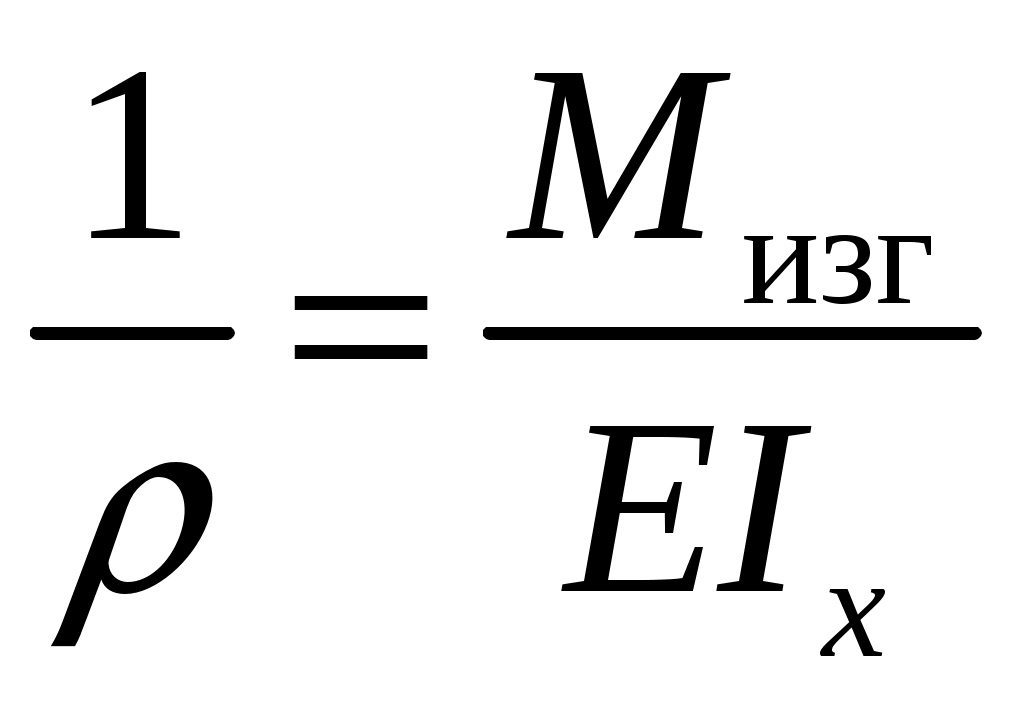

. (6.2)

Величина представляет собой кривизну нейтрального слоя балки, - жесткость балки на изгиб.

Итак, кривизна оси балки при изгибе пропорциональна изгибающему моменту и обратно пропорциональна жесткости балки.

Учитывая (6.1), исключим ρ, тогда получим связь между нормальным напряжением σ и изгибающим моментом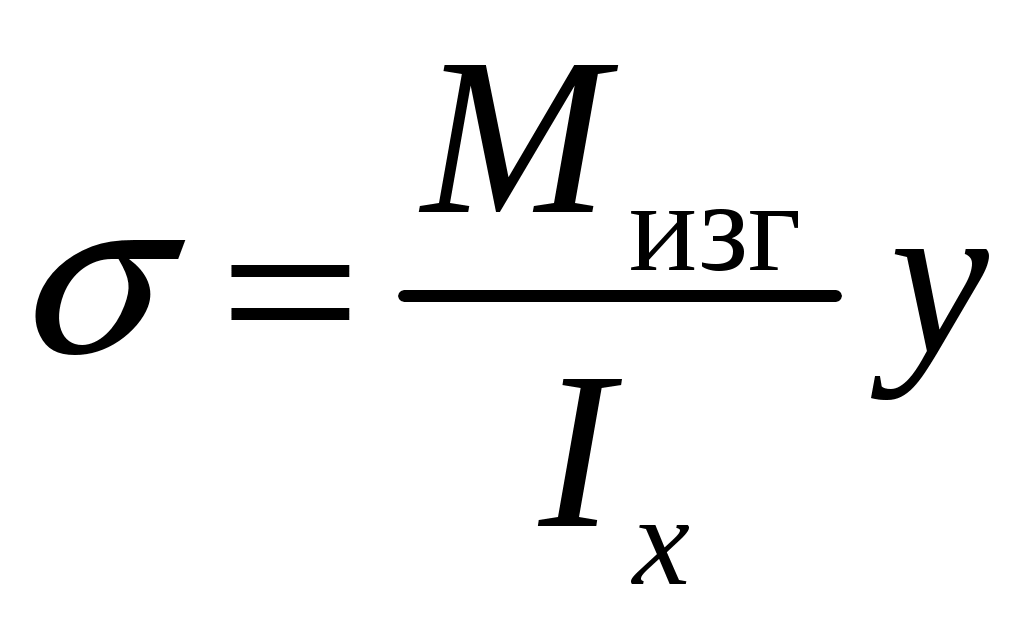

. (6.3)

Формула (6.3) позволяет определить величину нормального напряжения в любой точке поперечного сечения балки по известным изгибающему моменту и моменту инерции сечения.

Формула (6.3) получена для чистого изгиба. При действии на балку поперечных сил в сечениях кроме нормальных возникают и касательные напряжения. Однако неучет поперечных сил в расчетах по (6.3) мало сказывается для балок, у которых отношение высоты к длине не превышает 5%.

Эпюра нормальных напряжений в поперечном сечении балки согласно (6.3) имеет вид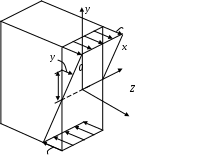




Из эпюры видно, что внутренние слои балки внутри нейтральной линии мало напряжены. Для экономии материала площадь сечения необходимо распределять подальше от нейтральной линии, то есть использовать сечения с большими моментами инерции относительно нейтральной линии. Наиболее рациональным оказывается применение прокатных профилей (двутавров, швеллеров и т.п.), рис. (а), (б).




(а) (б)
Условие прочности при изгибе
Условие прочности по нормальным напряжениям имеет вид:

,

где 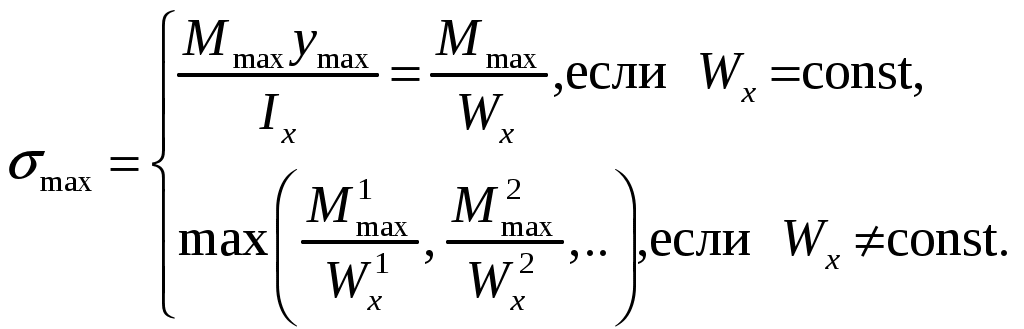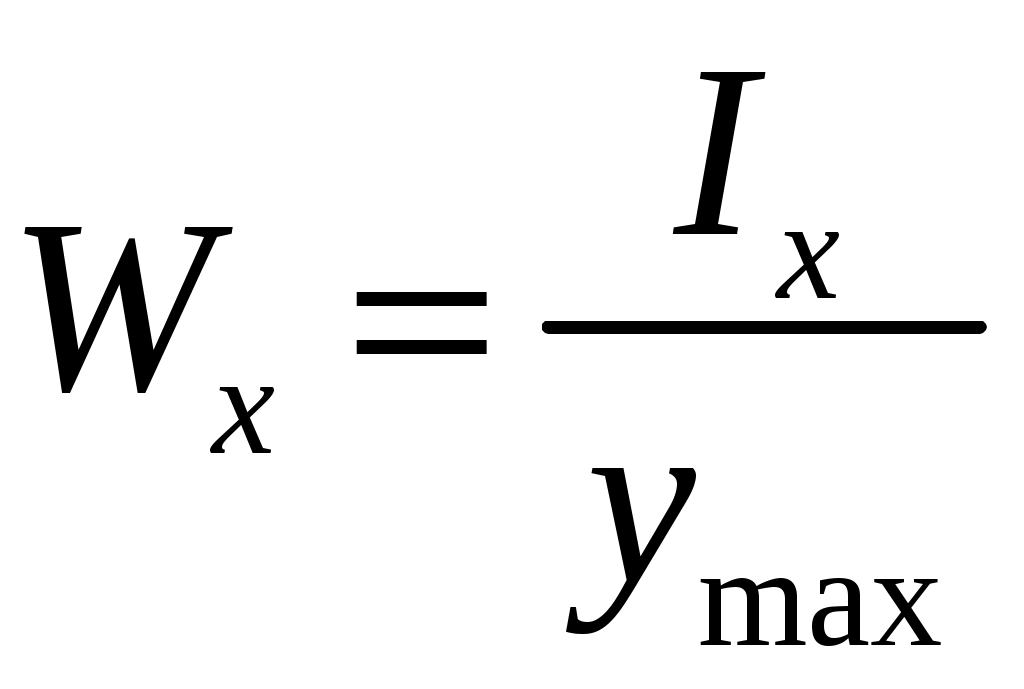согласно (6.3)



– максимальные изгибающие моменты, действующие в пределах каждого силового участка, - соответствующие моменты сопротивления. Момент сопротивления поперечного сечения рассчитывается как

.

Для прямоугольника со сторонами b, h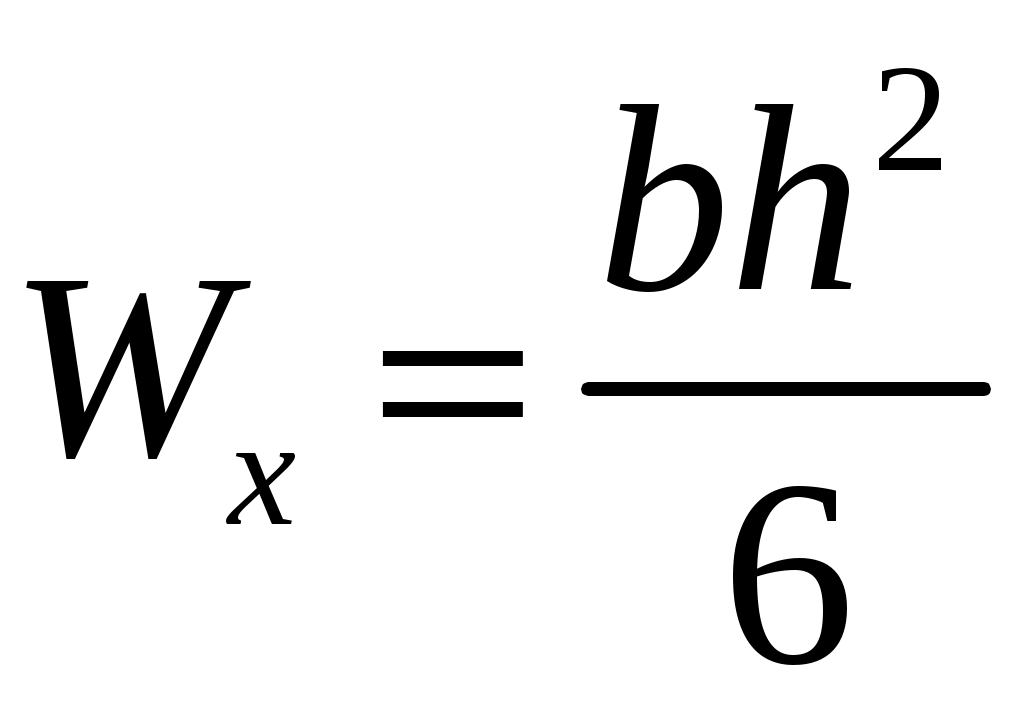

.

Для кольца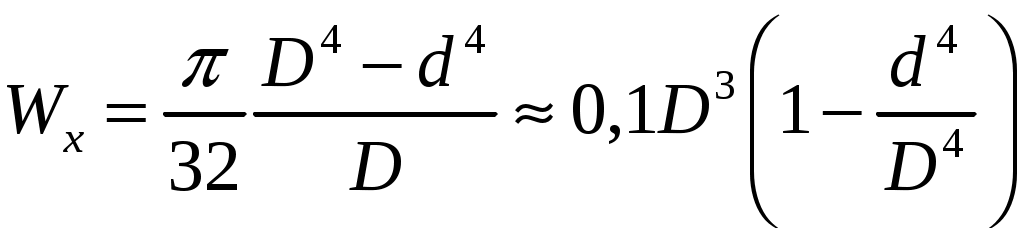

.

Определение касательных напряжений
В общем случае изгиба в поперечных сечениях балки возникают изгибающие моменты и поперечные силы. Наличие изгибающего момента связано с возникновением в поперечных сечениях балки нормальных напряжений, для определения которых можно пользоваться формулой (6.3).

Наличие поперечной силы обуславливает возникновение касательных напряжений в сечениях балки, а по закону парности касательных напряжений, и в ее продольных сечениях.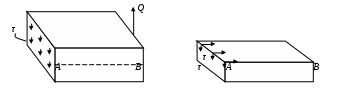



Закон распределения τ по высоте балки не известен.

Д 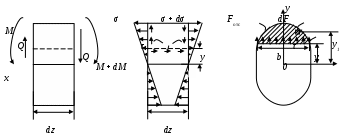ля расчета касательных напряжений выделим элемент dz по длине балки


(а) (б) (в)

Проведем горизонтальное сечение на расстоянии y от нейтральной линии и рассмотрим равновесие отсеченной части с основанием b, рис. (в), рис. (г). По закону парности сдвиговые напряжения в продольных сечениях равны сдвиговым напряжениям в поперечных сечениях.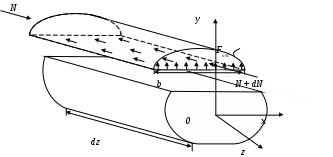



(г)
Рассмотрим условие равновесия отсеченной части

.

Последнее слагаемое есть сила, собираемая с площади продольного сечения bdz и обусловленная действием равномерно-распределенных по этой площади касательных напряжений τ. Из последнего уравнения выражаем τ

. (6.4)

С другой стороны, нормальная сила N есть равнодействующая нормальных напряжений, действующих по отсеченной площади поперечного сечения F_отс параллельно 0z

.

При этом сами нормальные напряжения выразятся как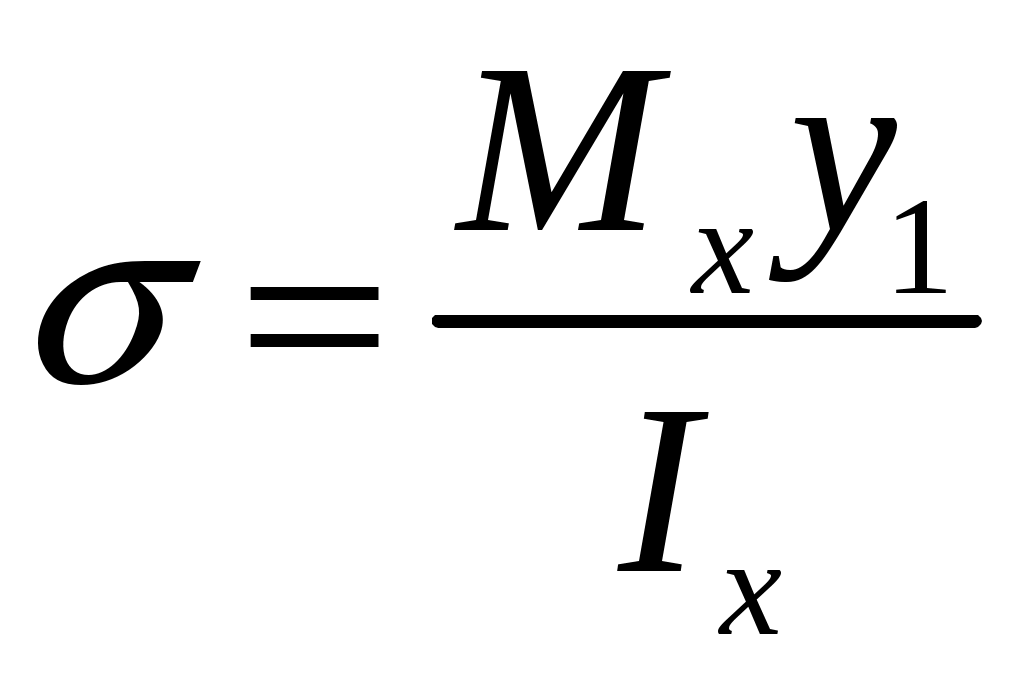

,

где 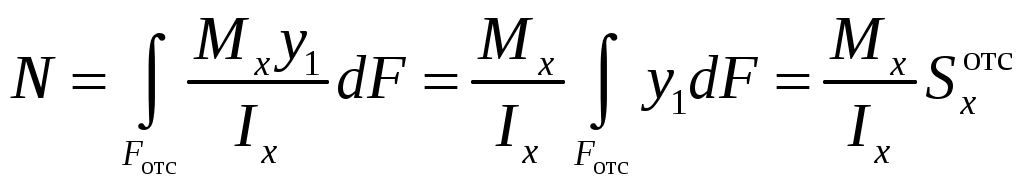, как и прежде, момент инерции поперечного сечения относительно оси x. Объединяя две последние формулы, получим

.

Здесь 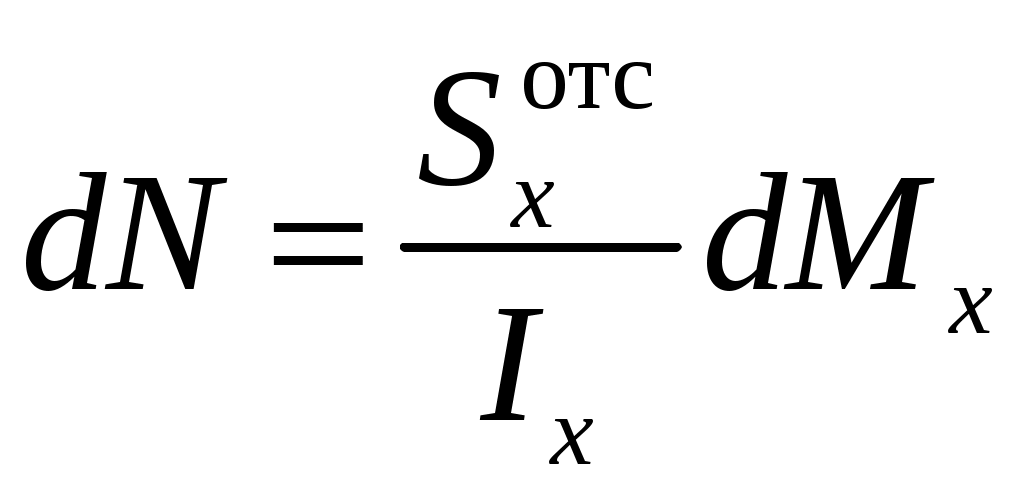- статический момент отсеченной площади относительно оси x. Дифференцируя последнее выражение, находим

.

Подставим последнее выражение в (6.4)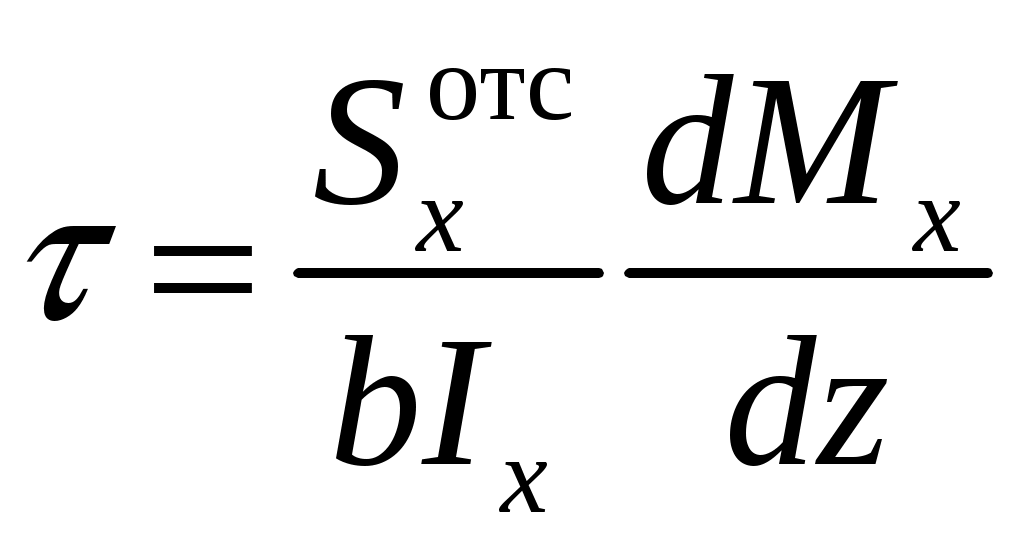

.

Вспоминая, что производная момента по длине балки согласно теореме Журавского есть поперечная сила Q_z, получим окончательное выражение для сдвиговых напряжений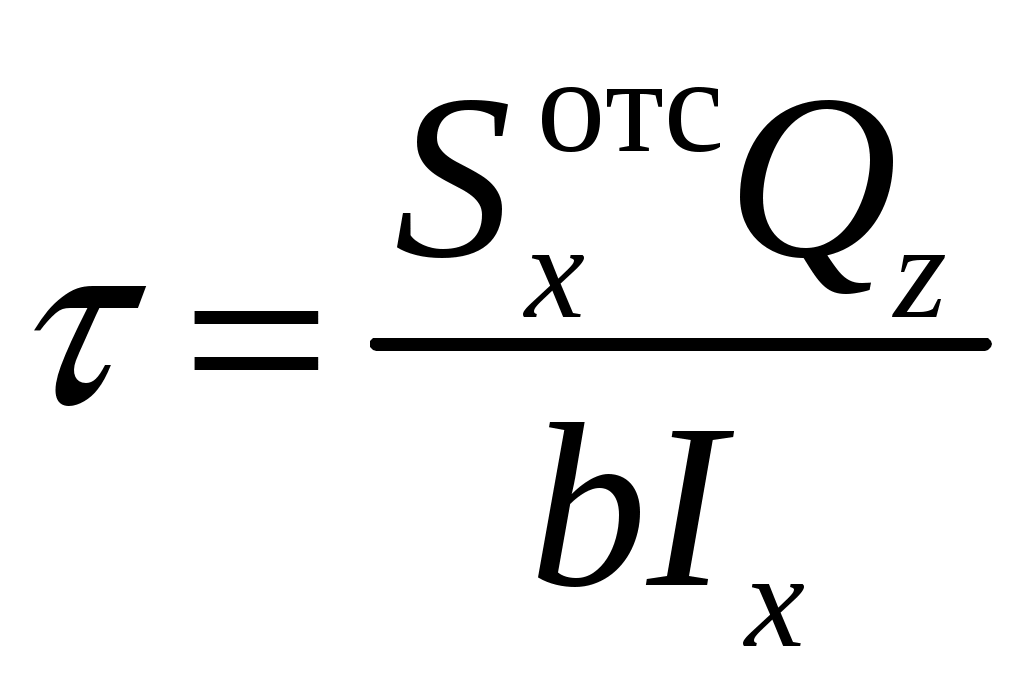

. (6.5)

Согласно (6.5), касательное напряжение может быть рассчитано для любого поперечного сечения балки, в котором известна поперечная сила Q_z. При этом сила Q_z и момент инерции I_x постоянны для каждого сечения. Переменными по координате y (отсчитываемой от нейтрального сечения по высоте балки) являются только и 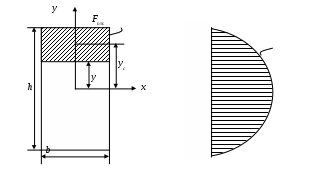b.

В качестве примера рассмотрим расчет τ для балки прямоугольного сечения, рис. (а).

(a) (б)

В данном примере по высоте сечения балки будут постоянны не только Q_z и I_x, но и ширина отсеченной части b. Статический момент отсеченной площади можно рассчитать как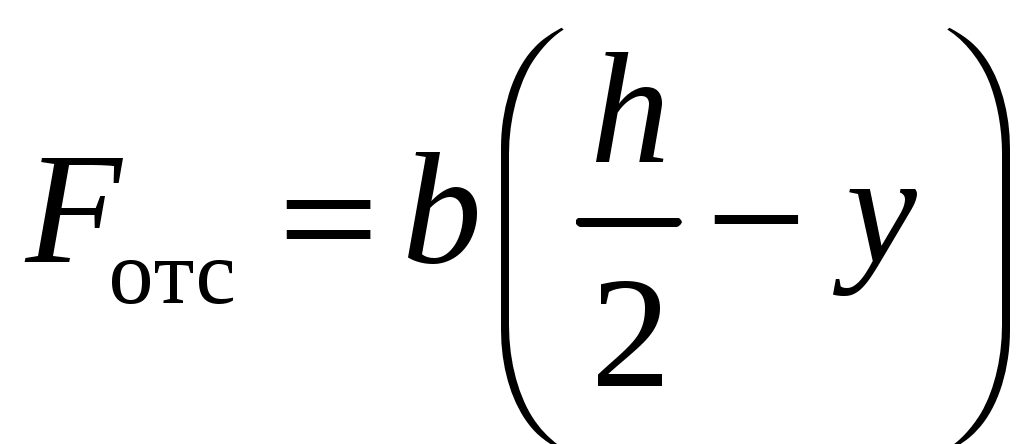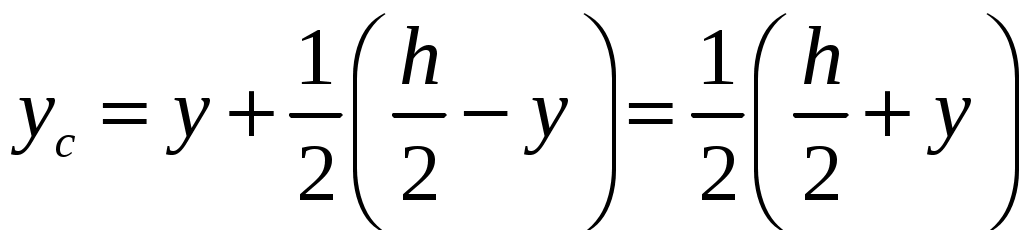

,

,

.

Подставляя выражения 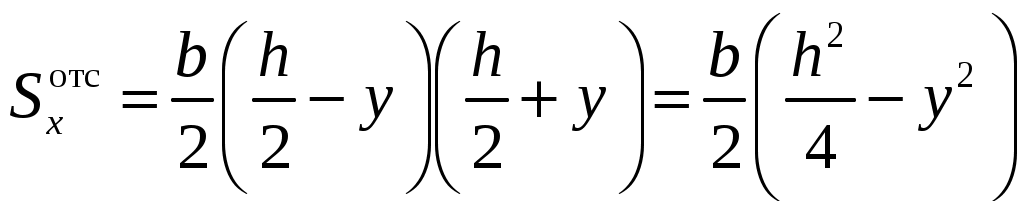и в выражение для , находим

.

Рассчитаем τ по (6.5)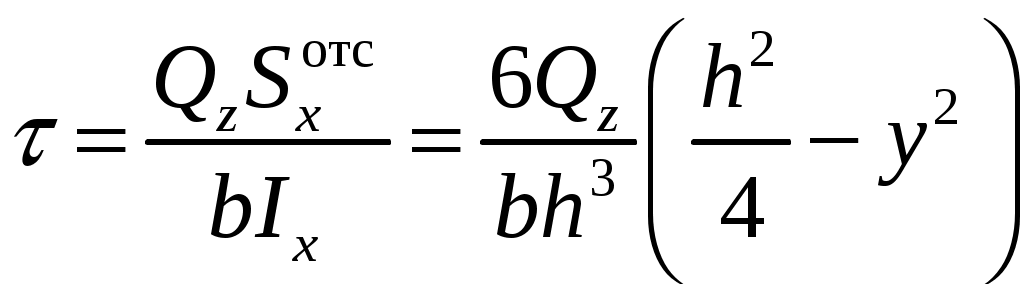

. (6.6)

Максимальное значение τ будет при y = 0 на нейтральном слое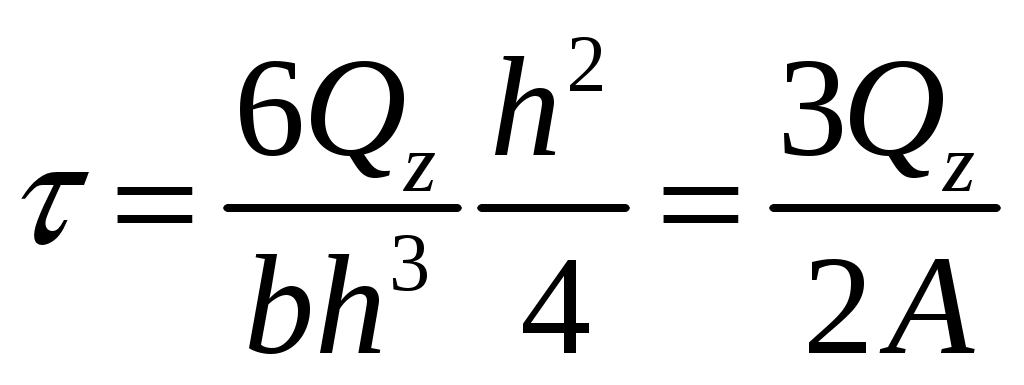

,

где A = bh. При этом согласно (6.6) касательные напряжения равны нулю на поверхности балки. Эпюра касательных напряжений приведена на рис. (б).
Деформации и перемещения при изгибе
При плоском изгибе ось балки искривляется, оставаясь в плоскости нагрузки. В результате каждое сечение (центр тяжести) получает вертикальное смещение (прогиб y) и поворачивается на некоторый угол
θ = arctg y', рис. (а).

θ m

E z

y
E' θ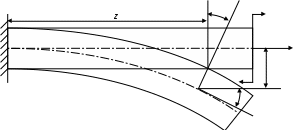




(а)

Угол θ, на который сечение поворачивается по отношению к своему первоначальному положению, называется углом поворота сечения. Учитывая, что повернувшееся сечение ортогонально изогнутой оси балки, заключаем, что вместо определения угла поворота сечения можно определить равный ему угол между касательной к изогнутой оси в данной точке и первоначальным положением балки.

Для определения деформации балки воспользуемся уравнением (6.2) для кривизны k нейтрального слоя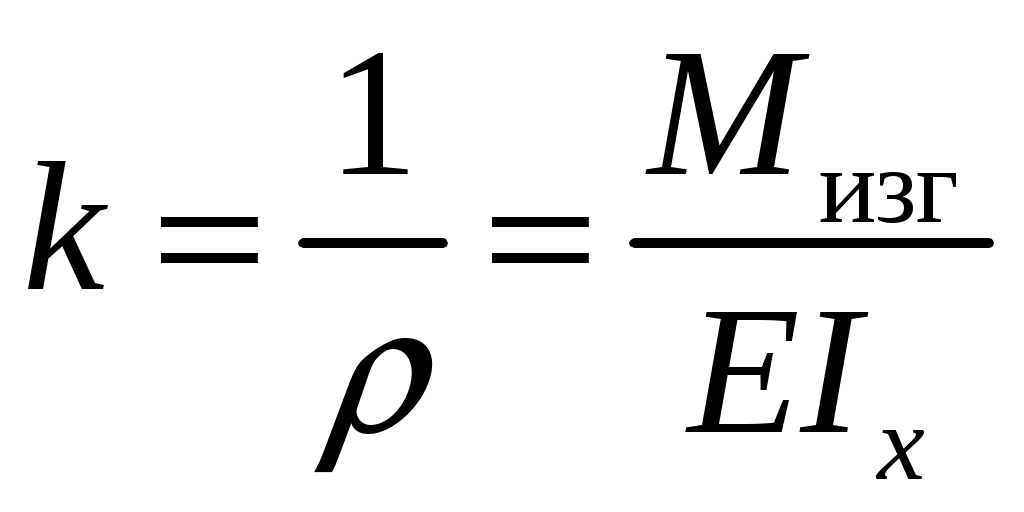

.

Как известно из курса высшей математики, выражение кривизны k через производные вертикального смещения имеет вид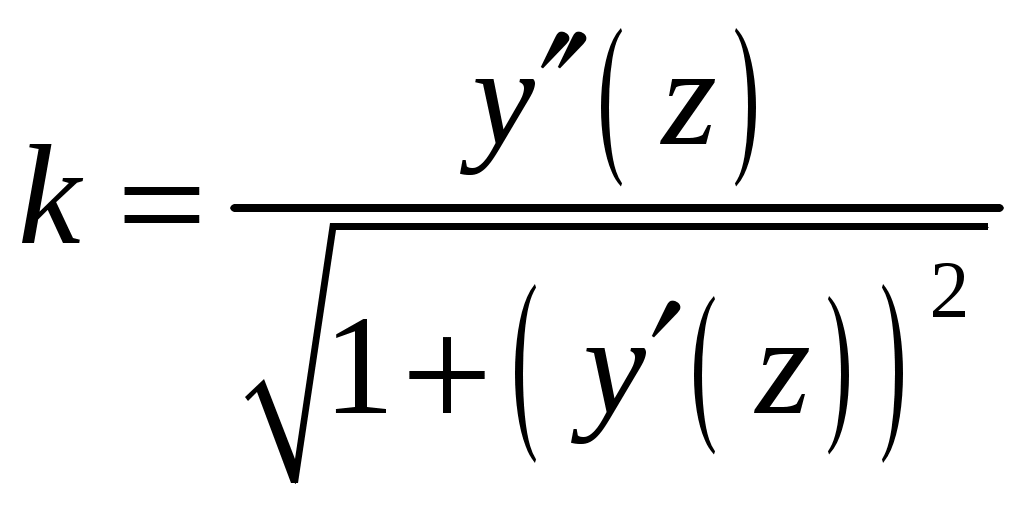

.

Ввиду малости по сравнению с единицей, принимаем

.

Отсюда получаем дифференциальное уравнение изогнутой оси балки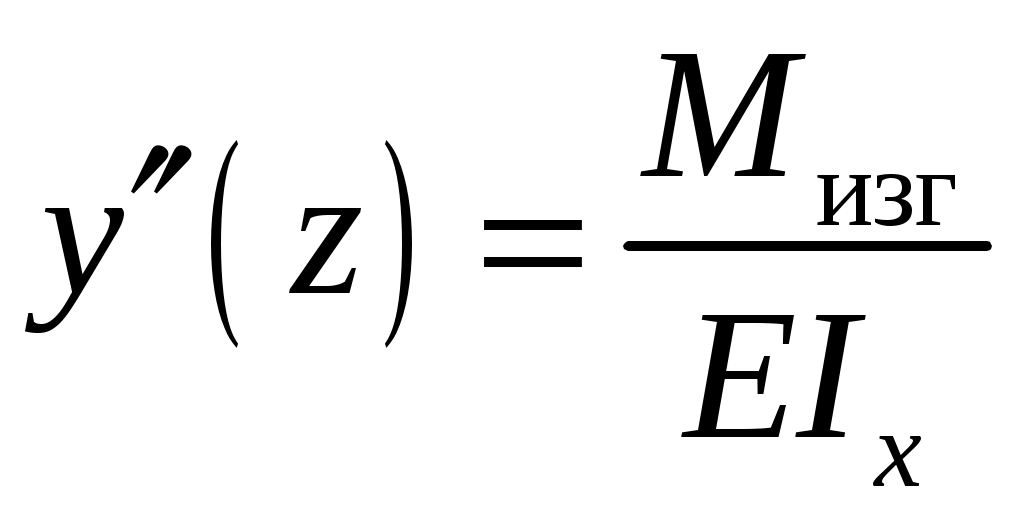

. (6.7)

Интегрируя (6.7) по z, получаем уравнение для углов поворота сечений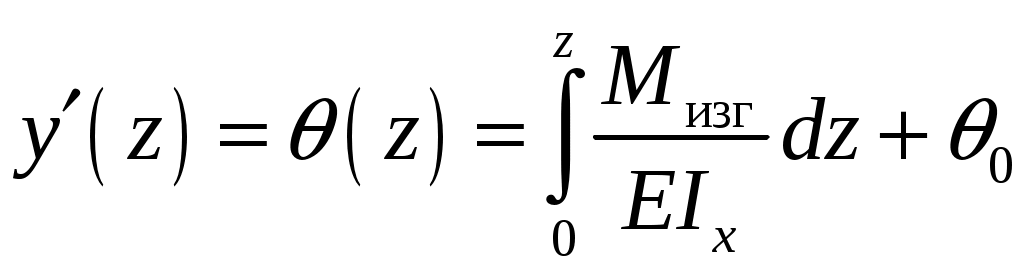

.

Повторное интегрирование дает уравнение изогнутой оси (прогибов)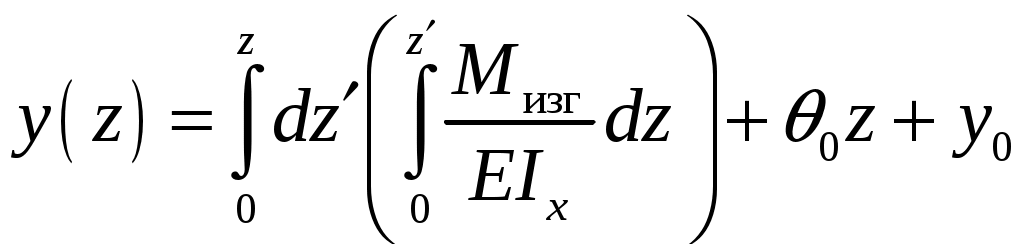

. (6.8)

Здесь константы - прогиб и угол поворота сечения в начале координат. Они определяются из условий опирания балки (граничных условий). Для балки, заделанной одном концом, в месте заделки должны быть равны нулю и прогиб, и угол поворота. Для балки, опертой по концам, прогиб должен быть равен нулю на каждой из опор.
Метод начальных параметров
Для решения дифференциального уравнения (6.8) воспользуемся методом начальных параметров.

Рассмотрим балку, нагруженную взаимоуравновешенной системой нагрузок.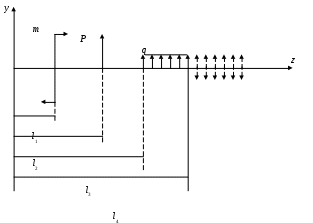




Будем рассматривать все участки балки в единой системе координат, помещая начало в крайнее левое, либо в крайнее правое сечение. Рассмотрим особенности, вносимые в уравнение упругой линии различными видами внешних нагрузок. Уравнения моментов по участкам будут следующими

1.

2.

3.

4.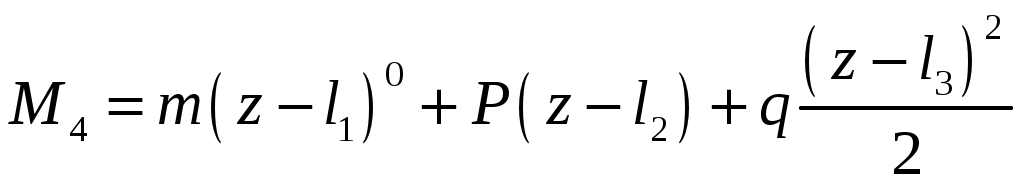

5.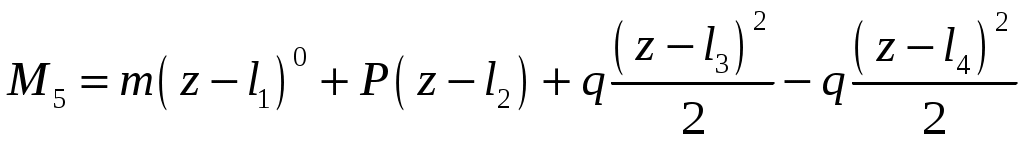

Заметим, что все моменты в 1-5 положительны.

В целях формализации процедуры интегрирования уравнения моментов по участкам имеют следующие особенности:

а) слагаемые, содержащие сосредоточенный момент m, умножены на , где - координата приложения m;

б) все распределенные нагрузки (в примере это нагрузка, приложенная в сечении и снятая в сечении ) продлеваются до конца балки;

в) в сечениях, где распределенная нагрузка отсутствует, но есть продленная, прикладывается компенсирующая нагрузка.

Уравнения моментов по участкам можно объединить в универсальное уравнение момента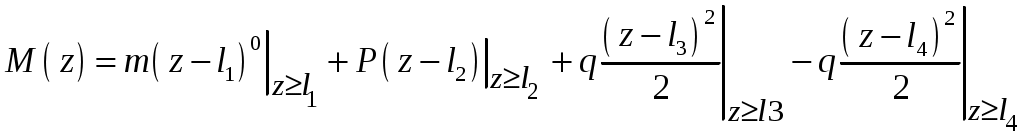

.(6.9)

Вертикальная черта и условие указывает на равенство нулю соответствующего слагаемого в случае, когда неравенство не выполнено. Например, первое слагаемое отсутствует в , если .

Интегрирование (6.9) дает универсальное уравнение углов поворота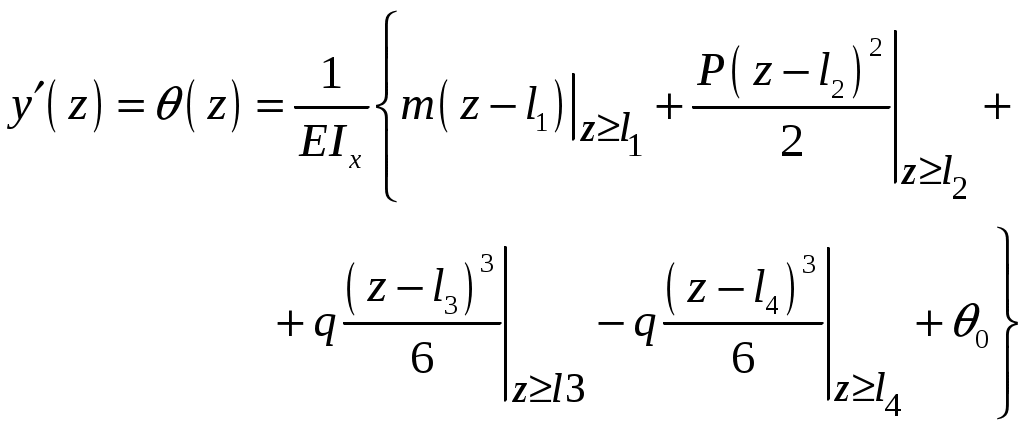

. (6.10)

Повторное интегрирование дает универсальное уравнение прогибов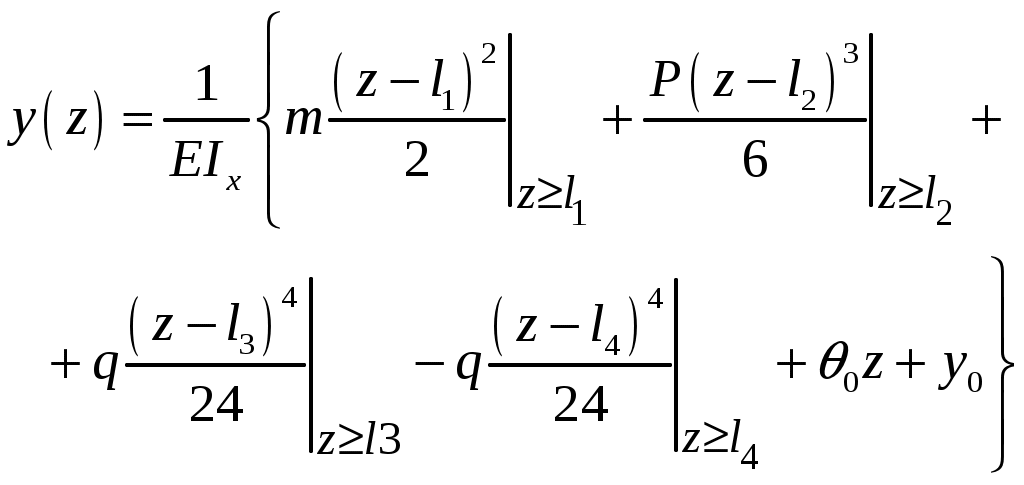

. (6.11)

Применение универсального уравнения позволяет значительно упростить решение, особенно для балок с несколькими участками.

Правила проверки правильности построения изогнутой оси балки основаны на связи изгибающего момента и кривизны балки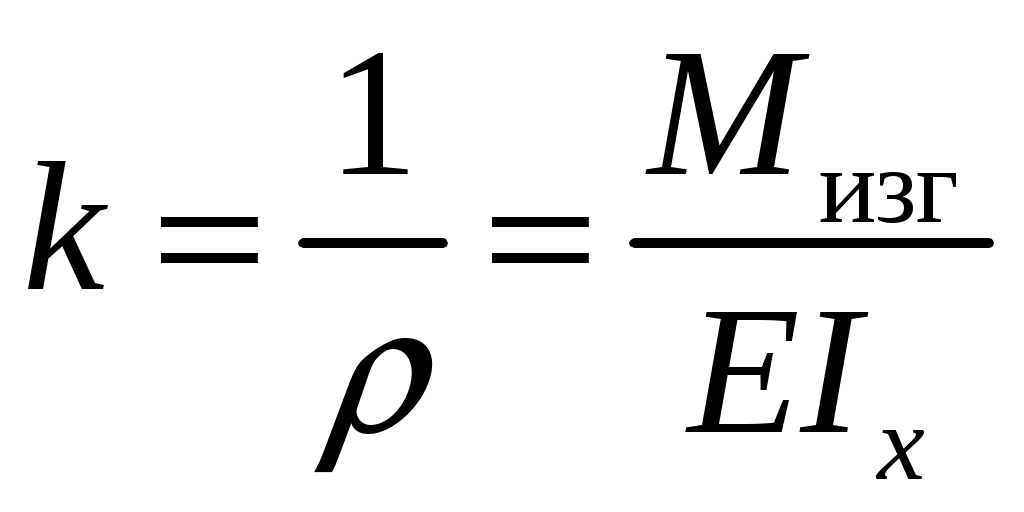

?

где ρ – радиус кривизны в сечении:

1) на участке, где изгибающий момент положителен, ось балки изогнута выпуклостью вниз;

2) на участке, где изгибающий момент отрицателен, ось балки изогнута выпуклостью вверх;

3) на участке, где M = 0, ось балки прямая линия;

4) в сечении где M = 0, у изогнутой оси балки – точка перегиба.

Условие жесткости при изгибе
Во многих случаях по эксплуатационным соображениям максимальные прогибы балок ограничиваются определенной величиной – допускаемым прогибом [y]. Тогда условие жесткости будет иметь вид:

.

Величина допускаемого прогиба зависит от назначения сооружения или механизма. Например, для подкрановых балок принимают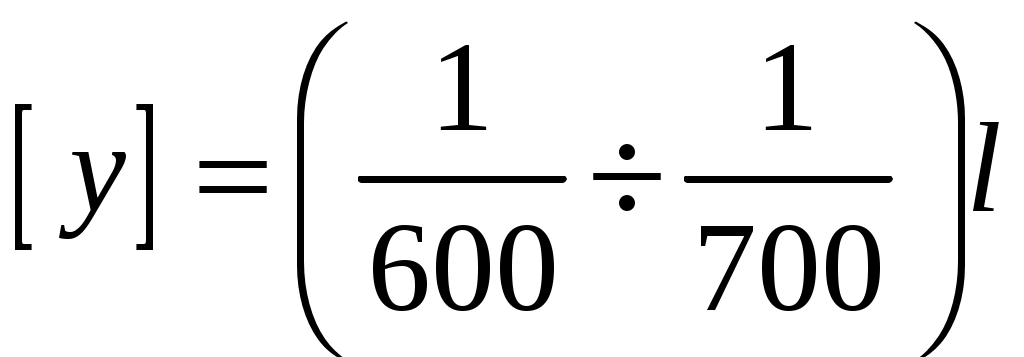

,

где l – пролет балки. В машиностроении норма допускаемого прогиба колеблется в зависимости от назначения детали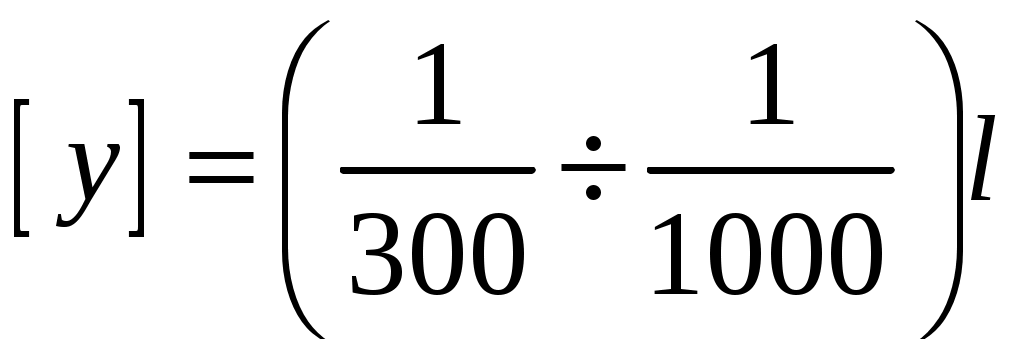

.