Главная страница
Навигация по странице:

  • Подготовительная часть.

  • Теоретическая часть.

  • Среднее 8,3265306 Дисперсия 9,2244898

  • Среднее =СРЗНАЧ(B2:B50) Дисперсия

    		•

    Лабораторные МКМ-1 (3). Задача об ассортименте продукции


    Скачать 1.49 Mb.
    НазваниеЗадача об ассортименте продукции
    Дата29.10.2022
    Размер1.49 Mb.
    Формат файлаdoc
    Имя файлаЛабораторные МКМ-1 (3).doc
    ТипЗадача
    #761230
    страница7 из 11
    1   2   3   4   5   6   7   8   9   10   11

    ЛАБОРАТОРНАЯ РАБОТА №6

    Получение и обработка результатов моделирования


    1. Подготовительная часть.

    Для выполнения лабораторной работы необходимо повторить следующие вопросы:

    1. Пуассоновское и показательное распределения случайной величины;

    2. Критерий согласия Колмогорова

    3. Методы получения результатов моделирования (метод подынтервалов, метод циклов)




    1. Теоретическая часть.

      1. Оценка статистических данных.


    Пример 1. В городе имеется транспортное агентство для обслуживания населения. Число заявок на обслуживание случайно и представлено выборкой 1. Время перевозок (включая время возвращения в гараж), так же случайно и представлено выборкой 2.

    Выборка 1 число заявок на перевозку за день

    Х1 =

    6
    3
    4
    11
    8
    6
    8
    12
    11
    8
    7
    16
    9
    11
    6
    11
    5
    8
    6
    12

    8
    7
    12
    6
    14
    6
    6
    9
    6
    7
    3
    3
    8
    9
    6
    14
    13
    9
    10
    12

    11
    4
    8
    9
    10
    8
    5
    8
    9


































    Выборка 2 Время обслуживания одной заявки в часах.

    Х2 =

    25
    52
    22
    7
    15
    55
    43
    11
    25
    24
    23
    24
    13
    15
    11
    38
    8
    18
    14
    73

    8
    48
    22
    4
    30
    6
    17
    12
    23
    112
    10
    45
    4
    32
    123
    39
    59
    19
    5
    12

    5
    7
    74
    57
    10
    35
    12
    28
    11
    16
































    Прежде чем приступить к исследованию данной системы, необходимо определить характеристики входного и выходного потоков.

    Во-первых, входящий поток должен являться простейшим (пуассоновским).

    Простейший поток обладает такими важными свойствами:

    1) Свойством стационарности, которое выражает неизменность вероятностного режима потока по времени. Это значит, что число требований, поступающих в систему в равные промежутки времени, в среднем должно быть постоянным.

    2) Отсутствия последействия, которое обуславливает взаимную не­зависимость поступления того или иного числа требований на обслужи­вание в непересекающиеся промежутки времени. Это значит, что число требований, поступающих в данный отрезок времени, не зависит от чис­ла требований, обслуженных в предыдущем промежутке времени.

    3) Свойством ординарности, которое выражает практическую невозмож­ность одновременного поступления двух или более требований (вероят­ность такого события неизмеримо мала по отношению к рассматриваемому промежутку времени, когда последний устремляют к нулю).

    Одним из признаков того, что случайная величина распределена по закону распределения Пуассона, является совпадение математического ожидания случайной величины и дисперсии этой же случайной величины, то есть:



    В качестве оценки для математического ожидания обычно выбирают выборочное среднее



    а в качестве оценки дисперсии - выборочную дисперсию: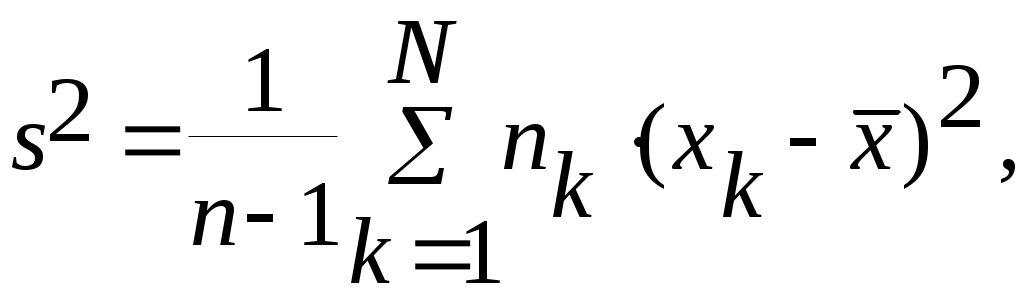



    где n - объём выборки X1={ };

    N - объём вариационного ряда;

    - частота в выборке Х1.
    Проведём расчёты (в Excel):


     
    выборка

     
    6

     
    3

     
    4

    …

     
    5

     
    8

     
    9

    Среднее__8,3265306__Дисперсия__9,2244898'>Среднее
    8,3265306

    Дисперсия
    9,2244898

    Отношение
    0,9026549




     
    выборка

     
    6

     
    3

     
    4

    …

     
    5

     
    8

     
    9

    Среднее
    =СРЗНАЧ(B2:B50)

    Дисперсия
    =ДИСП(B2:B50)

    Отношение
    =B51/B52
    1   2   3   4   5   6   7   8   9   10   11

    написать администратору сайта