Лабораторные МКМ-1 (3). Задача об ассортименте продукции
 Скачать 1.49 Mb.
|
|
Прежде чем приступить к исследованию данной системы, необходимо определить характеристики входного и выходного потоков. Во-первых, входящий поток должен являться простейшим (пуассоновским). Простейший поток обладает такими важными свойствами: 1) Свойством стационарности, которое выражает неизменность вероятностного режима потока по времени. Это значит, что число требований, поступающих в систему в равные промежутки времени, в среднем должно быть постоянным. 2) Отсутствия последействия, которое обуславливает взаимную независимость поступления того или иного числа требований на обслуживание в непересекающиеся промежутки времени. Это значит, что число требований, поступающих в данный отрезок времени, не зависит от числа требований, обслуженных в предыдущем промежутке времени. 3) Свойством ординарности, которое выражает практическую невозможность одновременного поступления двух или более требований (вероятность такого события неизмеримо мала по отношению к рассматриваемому промежутку времени, когда последний устремляют к нулю). Одним из признаков того, что случайная величина распределена по закону распределения Пуассона, является совпадение математического ожидания случайной величины и дисперсии этой же случайной величины, то есть:  В качестве оценки для математического ожидания обычно выбирают выборочное среднее  а в качестве оценки дисперсии - выборочную дисперсию: 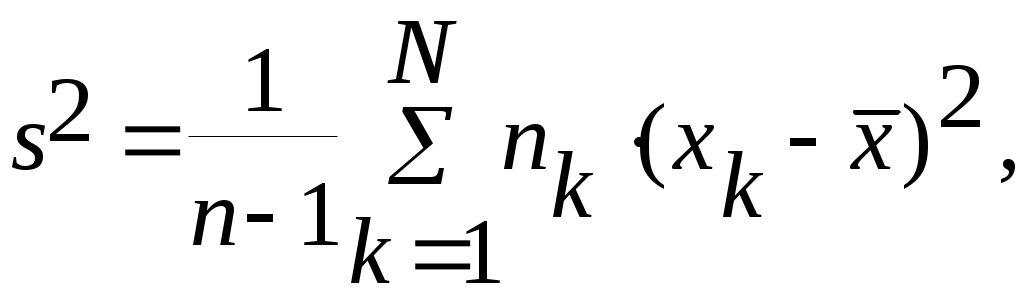 где n - объём выборки X1={  };N - объём вариационного ряда;  - частота  в выборке Х1.Проведём расчёты (в Excel):
Так как входной поток обладает всеми свойствами простейшего потока, а отношение математического ожидания и дисперсии близко к 1, можно сделать вывод о том, что входной поток распределен по закону Пуассона со средним λ=8. Во-вторых, время обслуживания заявок должно подчиняться экспоненциальному закону распределения. Показательный (экспоненциальный) закон распределения времени обслуживания имеет место тогда, когда плотность распределения резко убывает с возрастанием времени t. Например, когда основная масса требований обслуживается быстро, а продолжительное обслуживание встречается редко. Наличие показательного закона распределения времени обслуживания устанавливается на основе статистических наблюдений. Для проверки гипотезы о соответствии распределения эмпирической случайной величины теоретическому можно воспользоваться критерием А.Н.Колмогорова. Пусть задана выборка Х2=  случайной величины  , которая выражает длительность (время) обслуживания заявок одним из каналов исследуемой системы массового обслуживания. Выборка Х2 имеет объём n=50.Гипотеза Н0 заключается в том, что случайная величина имеет показательное распределение с параметром  , т.е. ,где  - оценка параметра показательного распределения  , которая находится как обратная величина к исправленному среднему выборочному  : , где  ,а  - элемент выборки Х2, выражает чистое время обслуживания k-той заявки, поступившей в систему массового обслуживания.Дальнейший этап исследования заключается в построении эмпирической функции распределения  . Для этой цели по выборке Х2 строится вариационный ряд  , где  - строго упорядоченные, а каждому значению  отвечает соответствующая ему частота , равная числу повторений в выборке Х2, причем выполняется тождество: .Тогда эмпирическую функцию распределения можно записать в виде: 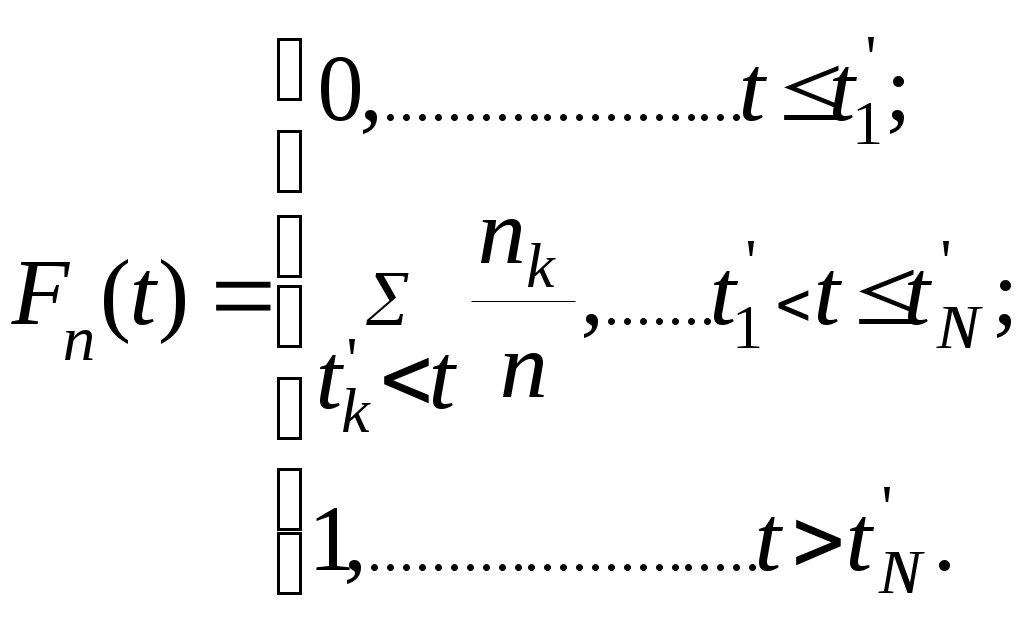  После того, как эмпирическая функция распределения построена, можно вычислить разности  в точках  , и  ,  ,  где  - достаточно малое число, скажем  . Далее проводим проверку гипотезы. По найденному значению  проверяется гипотеза Н0, сравнивая с величиной . Если   ., то гипотезу Н0 о том, что время обслуживания заявок подчинено показательному закону с параметром , можно считать не противоречащей опытным данным.Произведем расчеты (в Excel): Расчет параметра показательного распределения:
Построение эмпирической функции распределения. Для построения эмпирической функции распределения можно воспользоваться функцией пакета анализа Excel «Гистограмма». 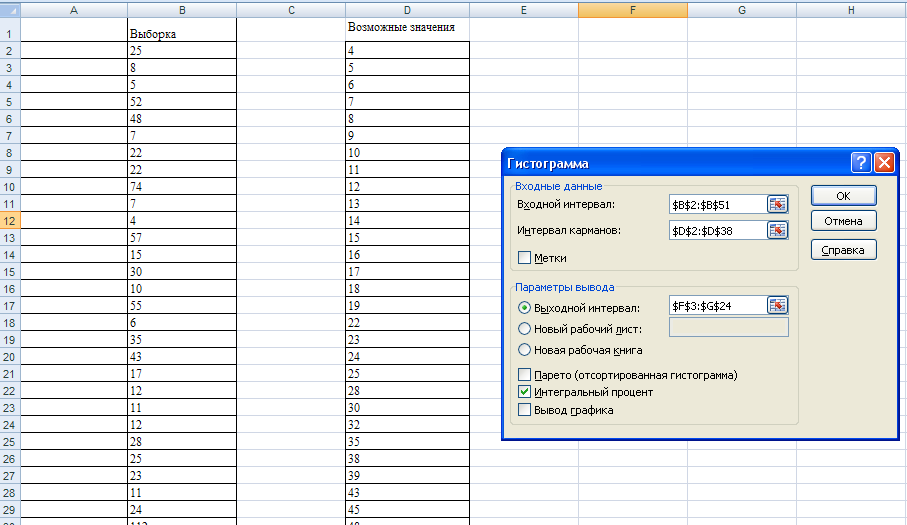 3. Вычисление разностей:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||