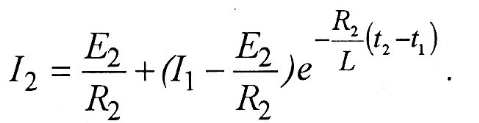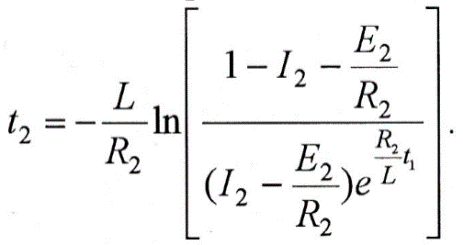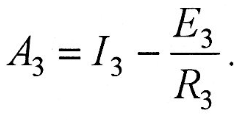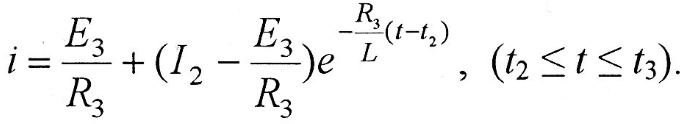Следует иметь виду, что нумерацию участков на характеристике начинают от точки, соответствующей значению функции тока i
(напряжения инс) при t = 0.
Подставляя уравнения отрезков прямых в исходное нелинейное дифференциальное уравнение, получаем: для первого участка
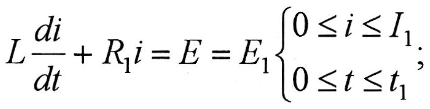
для второго участка
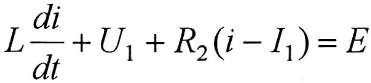
или
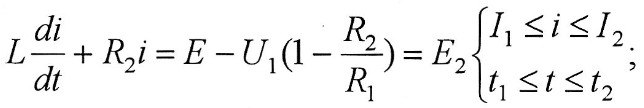
для третьего участка 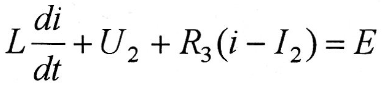
или 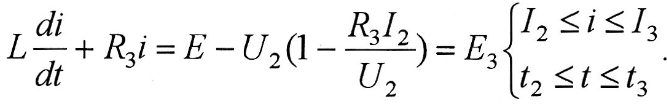
Полученные уравнения являются однотипными (неоднородные линейные дифференциальные уравнения первого порядка), поэтому общее решение этих уравнений имеет следующий вид:
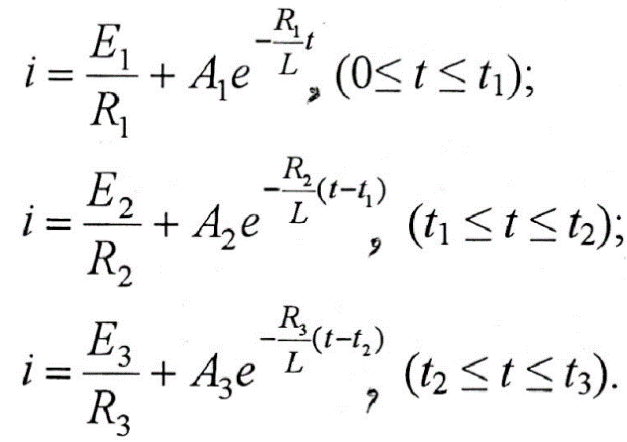
Далее определяются постоянные интегрирования и временной интервал
для каждого из уравнений. При этом используются как независимые начальные условия (законы коммутации), так и граничные значения функции
(значения токов и напряжений на нелинейном сопротивлении в точках излома В. А. X). Постоянная интегрирования А1находится из условия, что при t= 0, i(0) = 0 (используется первый закон коммутации), откуда
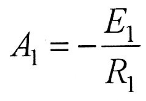
Окончательное выражение переходного тока на первом участке
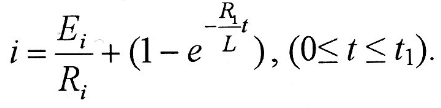
Если в это уравнение подставить вместо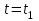 и и 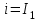 то можно определить момент времени то можно определить момент времени 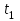 (временной интервал первого участка) (временной интервал первого участка)
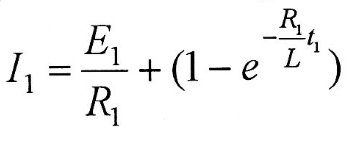
или 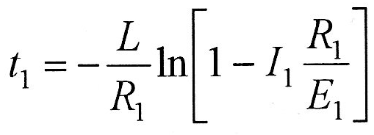
Постоянная  определяется из уравнения для тока второго участка при определяется из уравнения для тока второго участка при   следовательно, следовательно,
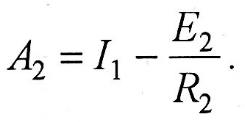
Уравнение тока для второго участка 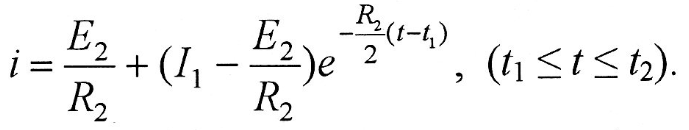
Момент времени t2находится из условия, что при t = t2, 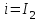 следовательно, следовательно,
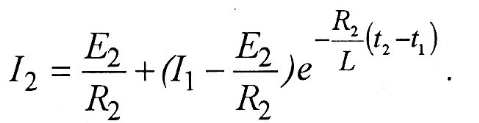
Полученное уравнение легко решается относительно t2
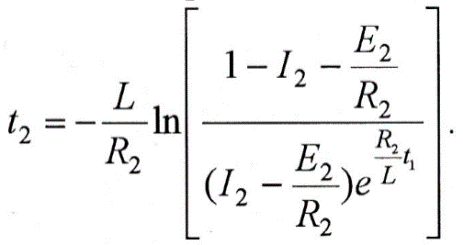
Наконец, постоянная интегрирования Азопределяется из уравнения тока для третьего участка при t = t2, i = I2
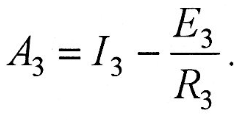
Окончательное уравнение переходного тока для третьего участка
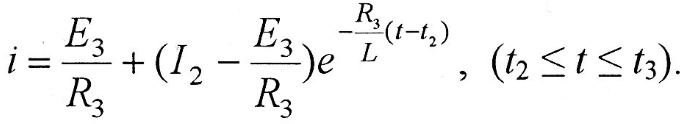
Из вышесказанного ясен порядок определения любого количества последующих постоянных интегрирования в случае большего числа участков.
По уравнениям для переходных токов различных участков построена кривая i =f(t) примерный характер которой показан на рис. 8.7.
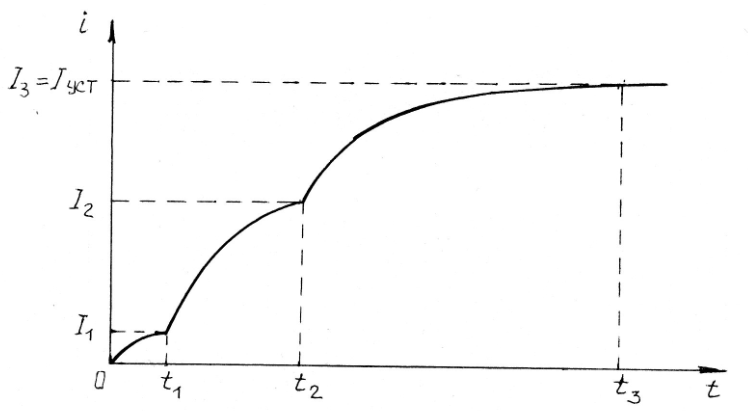
Рис. 8.7. Примерный характер динамической кривой
Метод аналитической аппроксимации
Предлагаемый метод основан на замене характеристики нелинейного
элемента аналитической зависимостью, достаточно точно отражающей нелинейность в рабочем диапазоне. Подстановка этой зависимости в нелинейное дифференциальное уравнение позволяет осуществить его интегрирование и получить аналитическое выражение искомой функции (переходного тока или напряжения на каком-либо элементе электрической цепи).
Следует иметь в виду, что аппроксимация характеристики нелинейного элемента аналитической зависимостью является отдельной задачей.
Возможны различные варианты аналитического представления нелинейной зависимости (степенным полиномом, логарифмической кривой и т. д.). При этом требуется исходить из того, чтобы процесс дальнейшего интегрирования дифференциального уравнения осуществился непосредственно и решение получилось в известных функциях. В противном случае будет отсутствовать точное аналитическое решение исходного дифференциального уравнения.
В качестве примера по данному методу рассмотрим коммутацию
(подключение) электрической цепи из последовательно соединенных ли постоянную э. д. с. (Е) источника электрической энергии (рис. 8.8, а).
|
 Скачать 4.06 Mb.
Скачать 4.06 Mb.
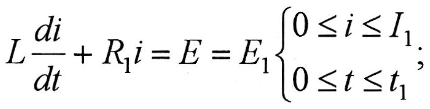
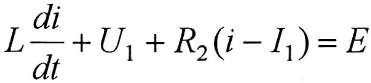
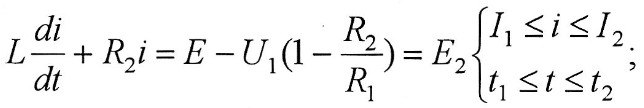
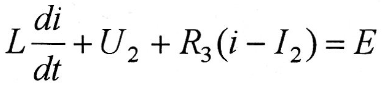
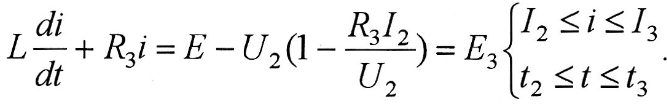
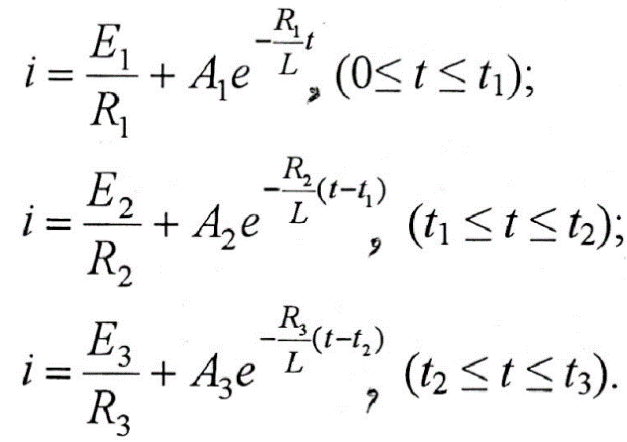
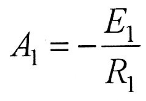
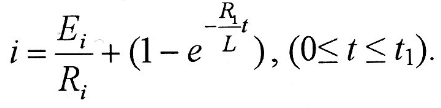
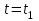 и
и 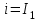 то можно определить момент времени
то можно определить момент времени 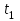 (временной интервал первого участка)
(временной интервал первого участка)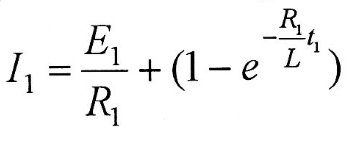
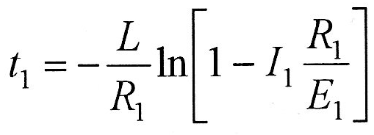
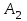 определяется из уравнения для тока второго участка при
определяется из уравнения для тока второго участка при 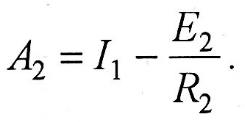
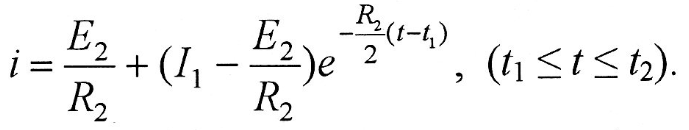
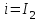 следовательно,
следовательно,