Практикум по Электротехника и электроника. Задача расчет линейных электрических цепей постоянного тока

• Название: Задача расчет линейных электрических цепей постоянного тока
• Дата: 06.03.2022
• Размер: 4.06 Mb.
• Имя файла: Практикум по Электротехника и электроника.docx
• Тип: Задача; #384302
• страница: 7 из 15

Задача 5. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ ПОСТОЯННОГО ТОКА

Условие задачи.

Для заданной электрической схемы из табл. 5.1 с известными пара­метрами (табл. 5.2) рассчитать переходный процесс классическим и опера­торным методами, определить законы изменений токов и напряжений во времени. Построить эти зависимости.
Последовательность решения классическим методом расчета.

Составить систему дифференциальных уравнений по законам Кирх­гофа для электрической цепи, получающейся после коммутации, при этом использовать соотношения u_L = Ldi/dt, i= Cdu_c/dt.

Подставить числовые значения заданных параметров в систему уравнений.

Решить систему уравнений относительно тока через индуктивность (напряжения на емкости), в результате получается неоднородное диффе­ренциальное уравнение первого порядка.

Решением неоднородного дифференциального уравнения является сумма частного (принужденная составляющая) и общего (свободная состав­ляющая) решения однородного дифференциального уравнения.

Принужденная составляющая определяется расчетом в послекоммутационной электрической цепи в установившемся режиме.

Свободная составляющая при решении однородных дифференциаль­ных уравнений первого порядка определяется как

Ae^pt

где А - постоянная интегрирования; р - корень характеристического урав­нения.

Характеристическое уравнение составляется по однородному диффе­ренциальному уравнению.

Последовательность решения операторным методом расчета.

Расчетные формулы и последовательность решения этим методом приведены в примерах расчета цепей, содержащих индуктивность и ем­кость.

Исходные данные к задаче 5

Таблица 5.1

Номер варианта	Значение параметров
	R1, Ом	R2, Ом	R3, Ом	R4, Ом	С, мкФ	L, мГн	U, B
1	50	-	50	-	170	-	100
2	25	25	25	-	.	125	100
3	25	25	25	-	40	-	100
4	50	50	50	-	-	250	100
5	50	50	50	50	60	-	100
6	50	50	50	-	-	250	100
7	25	25	25	-	180	-	100
8	50	50	50	-	-	125	100
9	25	25	25	25	100	-	100
10	25	25	25	-	-	250	100
11	50	50	50	-	90	-	100
12	25	25	25	-	-	250	100
13	25	25	-	-	110	-	100
14	25	25	-	-	-	125	100
15	20	50	10	50	-	125	100
16	50	10	50	15	260	-	100
17	50	25	50	-	-	125	100
18	50	50	50	-	120	-	100
19	50	50	50	-	-	125	100
20	25	-	25	-	190	-	100
21	25	50	25	-	-	125	100
22	50	50	50	-	-	125	100
23	50	50	50	-	60	-	100
24	50	50	50	-	180	-	100

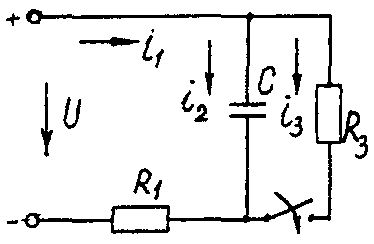
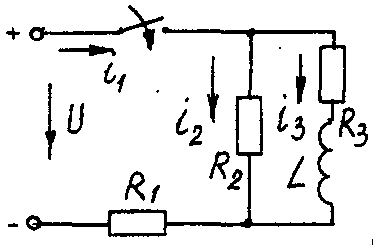
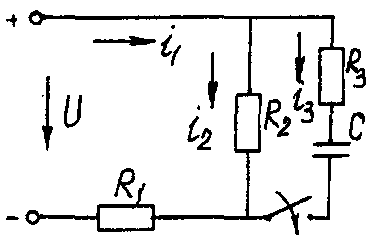
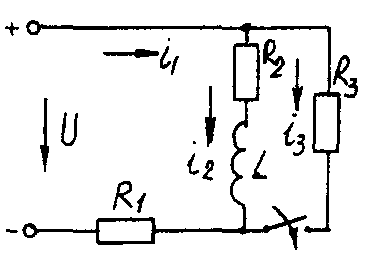
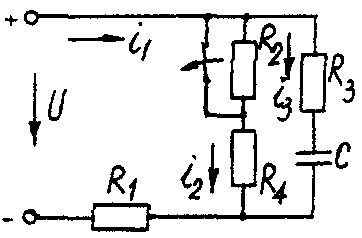
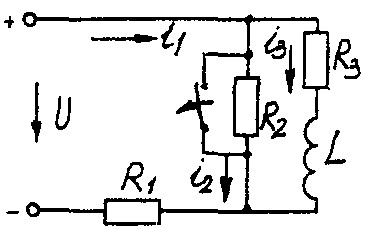
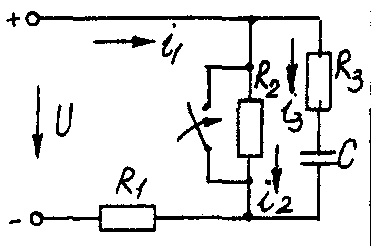
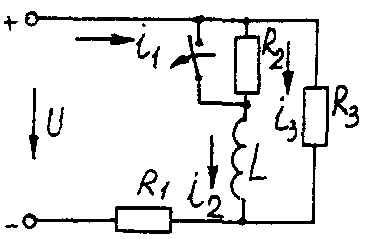
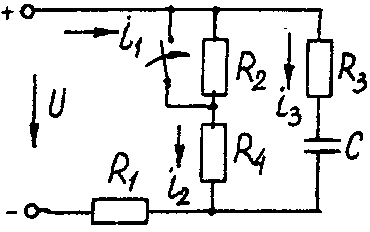
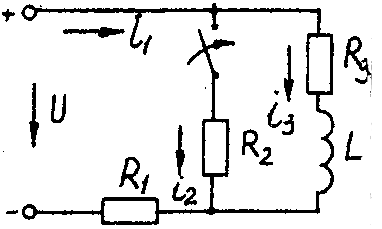
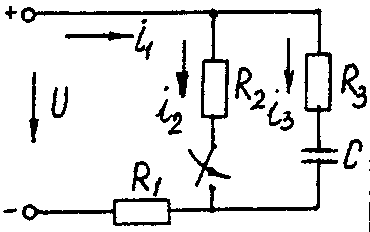
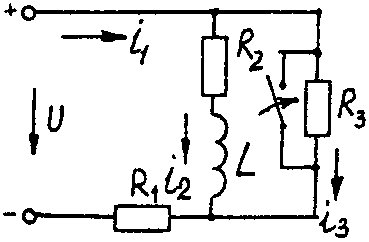
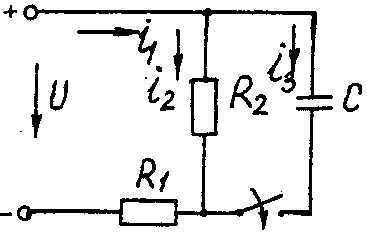
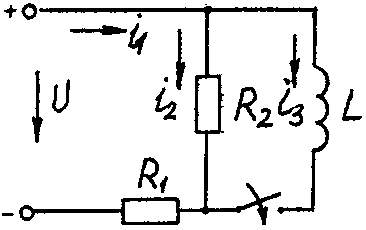
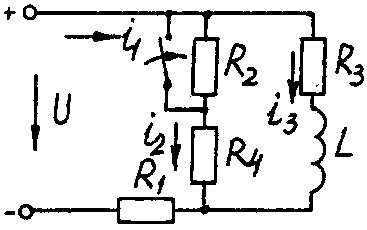
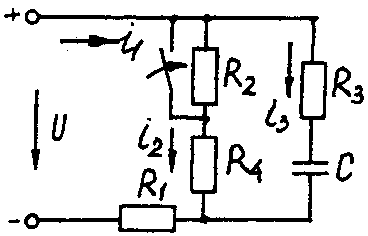
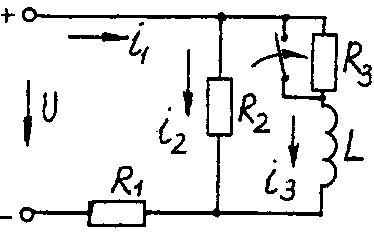
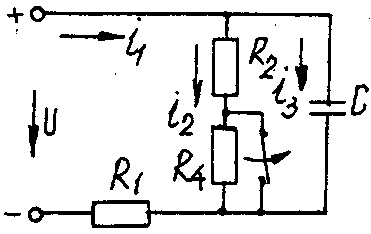
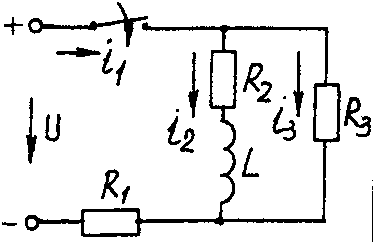
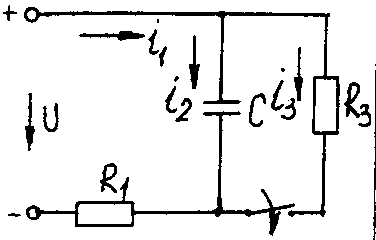
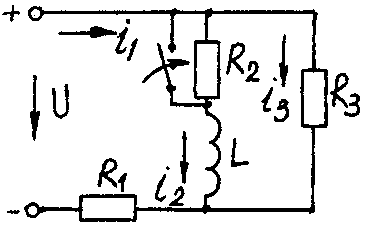
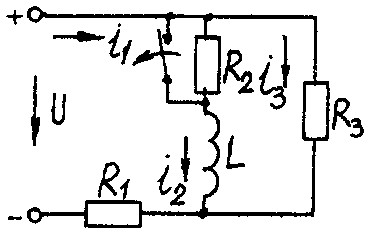
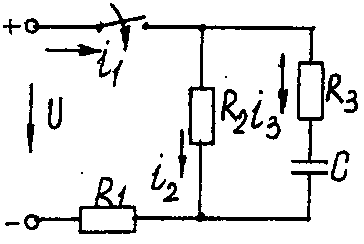
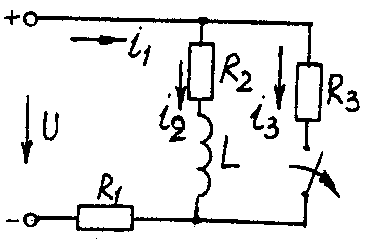
Электрические схемы для задачи 5

Таблица 5.2

№	Схема варианта	№	Схема варианта
1		2
3		4
5		6
7		8
Продолжение таблицы 5.2
9		10
11		12
13		14
15		16
Окончание таблицы 5.2
17		18
19		20
21		22
23		24

Последовательность решения операторным методом.
Расчетные формулы и последовательность решения этим методом приведены в примерах ресчета цепей, содержащих индуктивность и емкость.
Пример расчета цепи, содержащей индуктивность (рис. 5.1).

Исходные данные:
U= 100 В; R₁ = R₂ = R₃= R₄= 25 Ом; L= 0,25 Гн.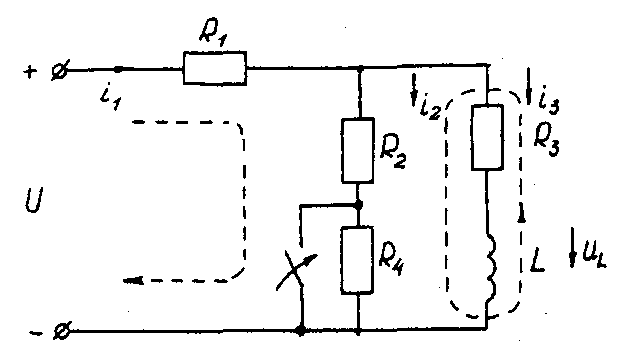



Рис. 5.1. Схема электрической цепи
Определить законы изменения токов, напряжения u_Lпри переходе це­пи от одного установившегося состояния к другому классическим и опера­торными методами. Построить эти зависимости.
Решение классическим методом.
Составляем систему дифференциальных уравнений по законам Кирх­гофа (три уравнения для определения трех неизвестных токов) для цепи, получающейся после коммутации: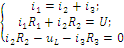

(5.1)

Решаем систему уравнений относительно тока через индуктивность i₃ (избавляемся от токов и )

(R₁+R₂) u_L + [R₁R₂ +R₁(R₁+ R₂)]i₃ =R₂U

Решение упрощается, если в систему уравнений (5.1) подставить за­данные числовые значения;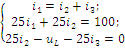

(5.2)

Решая систему уравнений (5,2), получаем

2u_L+75i₃=100. (5.3)

Подставив соотношение u_L= Ldi₃/dtв уравнение (5.3), получим

2Ldi₃/dt + 75i₃= 100,

и окончательно получаем неоднородное дифференциальное уравнение пер­вого порядка

di₃/dt + 150i₃=200. (5.4)

Решением уравнения (5.4) является сумма принужденной и свободной составляющих тока i₃(t)

i₃(t)= i₃(t)_пр+ i₃(t)_св. (5.5)

Принужденная составляющая тока определяется из уравнения (5.4) как новое установившееся значение по окончании переходного процесса

i₃(t)_пр = 200/150 =1,33 А. (5.6)

Запишем однородное дифференциальное уравнение первого порядка

di₃/dt+150 i₃= 0 (5.7)

и характеристическое уравнение

p+150=0. (5.8)

Свободная составляющая тока определяется как

i₃ (t)_св=Ae^pt, (5.9)

где А – постоянная интегрирования; р – корень характеристического урав­нения (5.8), р = -150; τ – постоянная времени электрической цепи, τ = 1/150.

Постоянная интегрирования определяется из начальных условий, ис­ходя из первого закона коммутации (ток через индуктивность при коммута­циях не меняется скачком).

С учетом уравнений (5.6) и (5.9) уравнение (5.5) запишем как

i₃ (t) = 1,33+А е^-150t.

Значение тока i₃(0) определяем, рассчитывая цепь до коммутации

i₃(0)=1,6А.

По первому закону коммутации i₃ (0) = i₃ (0)_пр + i₃ (0)_св⁼ 1,6 А, i₃(0) = 1,33 + А е^-150t = 1,6, откуда А = 1,6 – 1,33 = 0,27.

Окончательно

i₃ (t)= 1,33 + 0,27 е^-150t;

u_L(t)=Ldi₃/dt= 0,25-0,27(-150)е^-150t =-10е^-150t;

u₂(t) = [u₃(t)R₃+ u_L(t)]/R₂= 1,33 – 0,13 е^-150t;

i₁(t) = i₂(t) + i₃(t) = 2,66 + 0,14 е^-150t.
Решение операторным методом.

На рис. 5.2 представлена операторная схема замещения цепи (см. рис. 5.1).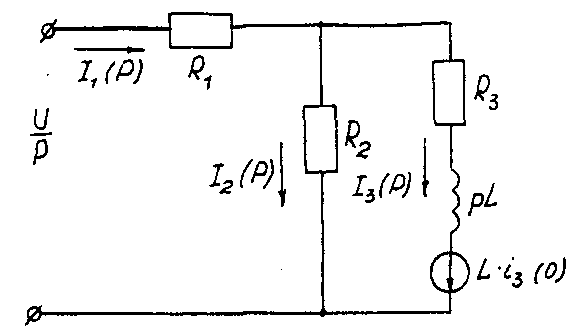

Составляется система уравнений в изображениях (в операторной фор­ме):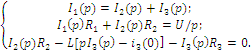
(5.10)
Рис. 5.2. Операторная схема замещения электрической цепи
Система уравнений решается относительно любого тока. Достаточно просто получаем уравнение в изображениях для тока через индуктивность, если использовать дифференциальное уравнение (5.4), из которого следует:

[pI₃(p) – i₃(0)]+150I₃(p)=200/p;

pI₃(p)+ 150I₃(p)= 200/p+ i₃(0)= 200/p+1,6

и окончательно

I₃(p)=(200+1,6p)/p(p+150)=F₁(p)/F₂(p), (5.11)

где F₁(p) – полином числителя; F₂(p) – полином знаменателя.

Переход от изображения тока I₃(p) к оригиналу i₃(t) осуществляем по формуле разложения

i₃(t)=Σ ([F₁(p)/F₂(p)]·е^Рк·t) (5.12)

где р_к– корни характеристического уравнения.

Характеристическим уравнением является полином знаменателя, рав­ный нулю, т. Е. F₂(p) ⁼ 0.

В рассматриваемом примере

P(p+150)=0,

откуда p₁=0; р₂= -150.

Производная полинома знаменателя

F₂'(p)=(2p+150),

откуда F₂'(p₁)=150; F₂'(p₂)= -150.

Оригинал тока i₃(t)

i₃(t)= ([F₁(p₁)/F₂’(p₁)] ·е^Р1·t)+ ([F₁(p₂)/F₂’(p₂)] ·е^Р2·t)=

= [(200 +1,6 0) / 150]e^150t+ [(200 +1,6 (-150) / (-150)]·e^-150·t =

= 1,33 + 0,27 e^-150t.

На рис. 5.3 представлены переходные характеристики токов и напря­жения на индуктивности.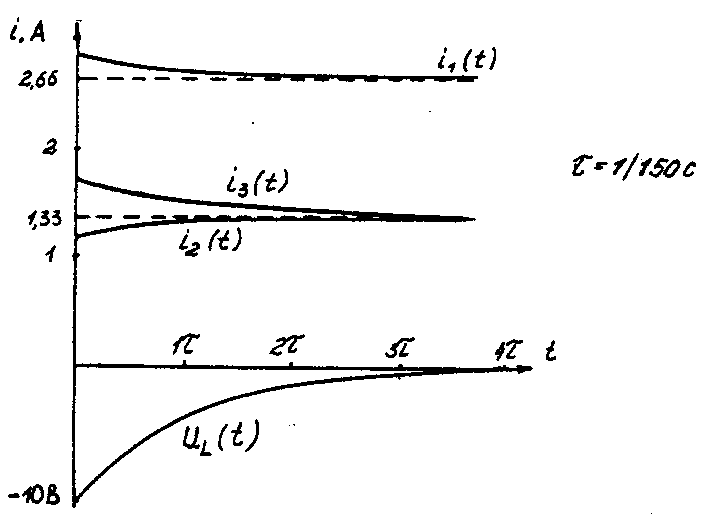



Рис. 5.3. Временные диаграммы токов и напряжения на индуктивности
Пример расчета цепи содержащей емкость (рис. 5.4).
Исходные данные:

U= 100 В; R₁= R₂= R₃ = 50 Ом; С = 100 мкФ.

Определить и построить следующие зависимости: u_C(t), u₁(t), u₂(t), u₃(t).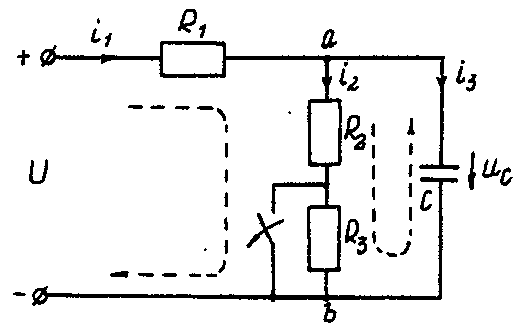


Рис. 5.4. Схема электрической цепи

Решение классическим методом.

Составляем систему дифференциальных уравнений по законам Кирх­гофа (три уравнения для определения трех неизвестных токов) для цепи, получающейся после коммутации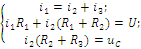

(5.13)

Между током и напряжением на емкости существует соотношение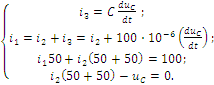

(5.14)

Решаем систему уравнений (5.14) относительно напряжения на емкости

du_c / dt+300и_с = 20000. (5.15)

Уравнение (5.15) – неоднородное дифференциальное уравнение пер­вого порядка.

Решением уравнения (5.15) является сумма принужденной и свобод­ной составляющих напряжения u_C(t). Решение неоднородного дифферен­циального уравнения первого порядка рассмотрено выше для цепи с индук­тивностью. По аналогии имеем

u_C(t)= u_C(t)_пр+u_C(t)_св. (5.16)

Принужденная составляющая напряжения равна

u_C(t)_пр= 20000/300 = 66,7 В.

Свободную составляющую напряжения находим из уравнения

u_C(t)_СВ=Ae^pt,

где (р + 300) = 0 – характеристическое уравнение; р = -300 – корень харак­теристического уравнения; τ – постоянная времени электрической цепи, τ= 1/300; u_C(0) = 50 В, напряжение и_Cвмомент коммутации (определяется расчетом рассматриваемой цепи до коммутации):

u_C(t)=66,7+Ae^-300t;

u_C(0)= 66,7+Ae^p·0 = 50В, откуда А = -16,7.

Окончательно имеем:

u_C(t)=66,7-16,7·e^-300t;

i₃(t)=C·du_C/dt=100·10^-6(-16,7)(-300)·e^-300t=0,5·e^-300t ;

i₂(t)=u_ав(t)/(R₂+R₃)=u_C(t)/(R₂+R₃)=0,667-0,167·e^-300t;

i₁(t)=i₂(t)+i₃(t)=0,667+0,333·e^-300t.

На рис. 5.5 представлены переходные характеристики токов и напря­жения на емкости.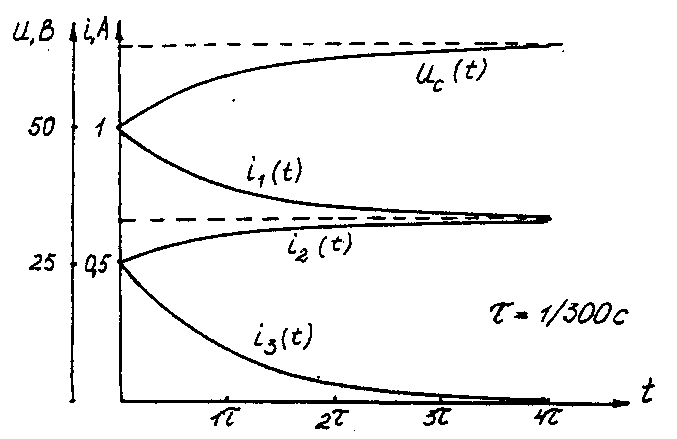



Рис. 5.5. Временные диаграммы токов и напряжения на емкости
Решение операторным методом.
Система уравнений в изображениях (в операторной форме) может быть составлена по операторной схеме замещения (рис. 5.6) или по системе дифференциальных уравнений (5.14)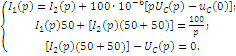

(5.17)

Решаем систему алгебраических уравнений (5.17) относительно токов или напряжения на емкости U_C (p).

Решение относительно напряжения U_C(p) упрощается, если восполь­зуемся уравнением (5.15). Уравнение (5.15) преобразуем в уравнение в изо­бражениях:

[pU_C(p)-u_C(0)]+300·U_C(p)=20000/p;

Uc (p)(p+ 300) = 20000/р + 50;

U_c (р) = [20000 + 50р] /р(р + 300) = F₁(p)/ F₂(p),

где F₁(p) – полином числителя; F₂(p) – полином знаменателя.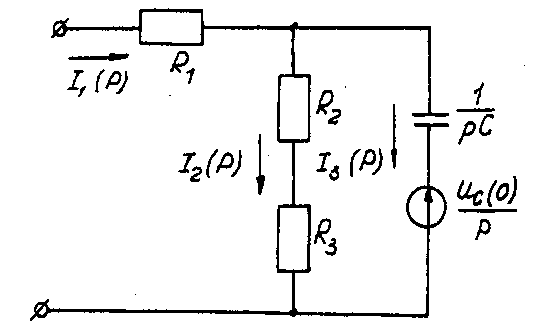

Рис. 5.6. Операторная схема замещения электрической цепи
Переход от изображения напряжения U_C(p) к оригиналу u_C(t) осуще­ствляем по формуле разложения

U_C(t)=Σ([F₁(p)/F₂'(p)] ·е^Рк·t) (5.18)

где р_к– корни характеристического уравнения.

Характеристическим уравнением является полином знаменателя рав­ный нулю, т. Е. F₂(p) = 0.

В рассматриваемом примере

p(p+300)=0,

откуда р₁= 0; р₂= -300.

Производная полинома знаменателя

F₂'(p)=(2p+300),

откуда F₂'(p₁)=300; F₂'(p₂)=-300.

Оригинал напряжения u_C(t)

u_C(t) = ([F₁(p₁)/ F₂'(p₁)] ·е^Р1·t) +([F₁(p₂)/F₂'(p₂)] ·е^Р2·t)=

=[(20000 + 50 0) / 300]·e^300·0 + [(20000+50 (-300) / (-300)]·e^-300t=

= 66,7 – 16,7·e^-300·t.