Практикум по Электротехника и электроника. Задача расчет линейных электрических цепей постоянного тока

• Название: Задача расчет линейных электрических цепей постоянного тока
• Дата: 06.03.2022
• Размер: 4.06 Mb.
• Имя файла: Практикум по Электротехника и электроника.docx
• Тип: Задача; #384302
• страница: 6 из 15

Методические указания.

Задачу решить комплексным методом, совместив один из векторов фазного или линейного напряжений источника энергии с положительным направлением оси вещественных чисел. Для определения линейных и фаз­ных токов и напряжений второго приемника рекомендуется провести эк­вивалентные преобразования треугольника в звезду.

Последовательность решения.

Записать линейные и фазные напряжения источника энергии в ком­плексной форме. Провести соответствующие эквивалентные преобразова­ния второго приемника. Определить линейные токи приемников при от­ключенной батарее конденсаторов. Определить падение напряжений в про­водах линии электропередачи Z_Л2. Определить фазные токи второго прием­ника. Определить реактивную мощность в фазе батареи конденсаторов, не­обходимую для повышения коэффициента мощности приемников до еди­ницы. Определить емкость и ток в фазе батареи конденсаторов. Определить линейные токи источника энергии при включении батареи конденсаторов. Построить векторную топографическую диаграмму напряжений и вектор­ную диаграмму токов источника энергии и приемников.
Пример решения задачи

Для заданной электрической схемы трехфазных потребителей (рис. 4.1) по известным параметрам: U_Л= 220 В; Z_Л1= 1,7 Ом; Z_Л2= (1,4+j1,6) Ом; Z₂= (9+j7) Ом; Р₁= 4 Вт; cos φ₁=0,7; определить линейные и фазные токи и напряжения приемников при отключенной батарее конденсаторов и при включении ее; реактивную мощность в фазе батареи конденсаторов, необ­ходимую для повышения коэффициента мощности приемников до едини­цы; емкость и ток в фазе батареи конденсаторов. Построить векторную то­пографическую диаграмму напряжений и векторную диаграмму токов ис­точника и приемников электрической энергии.

1. Выразим линейные и фазные напряжения источника энергии в ком­плексной форме, В

U_ф= U_л / √3=220 / √3=127.

Вектор фазного напряжения источника венных чисел, тогда, В

Ů_A направим по оси вещественных чисел, тогда, В

Ů_A= Ů_Ф=127;

Ů_B= Ů_A·e^-j120°=127· e^-j120°;

Ů_C= Ů_A·e^-j120°=127· e^j120°;

Ů_AB= Ů_A·- Ů_B =127·127· e^-j120°=220e^j30°;

Ů_CA= Ů_C- Ů_A =127· e^j120°-127=220e^j150.

2. Преобразуем треугольник сопротивлений а,b, с второго приемника (рис. 4.2) в эквивалентную звезду, Ом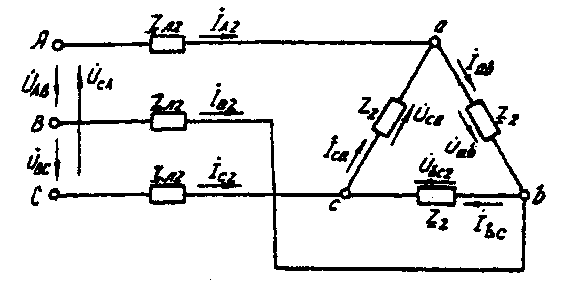


Рис. 4.2. Треугольник сопротивлений второго приемника
Поскольку приемник симметричный, то сопротивление фазы эквива­лентной звезды в три раза меньше сопротивления фазы треугольника.

Для симметричных приемников, соединенных в звезду, потенциалы нулевых точек должны быть одинаковыми. В связи с этим дальнейший рас­чет выполним для одной фазы (фазы А) (рис. 4.3).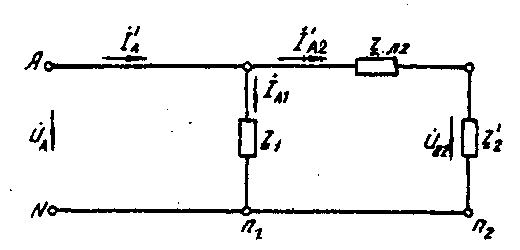


Рис. 4.3. Расчетная схема токов в фазе А
Полное сопротивление фазы эквивалентной звезды с учетом сопро­тивления линия Z_Л2 равно, Ом.

3. Определить линейные и фазные токи и напряжения второго прием­ника, а также полную мощность одной его фазы при отключенной батарее конденсаторов.

Фазные токи эквивалентной звезды, А: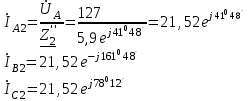



Фазные токи эквивалентной звезды (рис. 4.4) равны линейным токам треугольника второго приемника (см. рис. 4.2).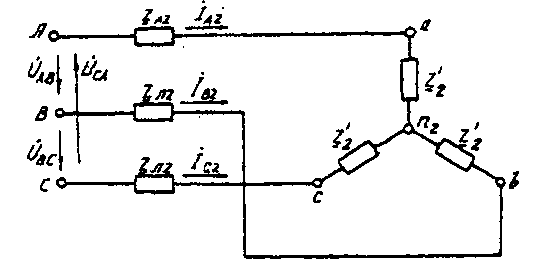



Рис. 4.4. Эквивалентная звезда второго приемника

Фазные напряжения эквивалентной звезды, В:

Ů_a2=Ů_A–İ_A ·Z_Л2=127-21,52e^-j41°48'·2,13e^j48°49'=81,59 – j5,58=81,78e^-j3°55';

Ů_b2 = 81,78e^-j123°55';

Ů_с2 =81,78e^j116°05'.

Линейные напряжения эквивалентной звезды, В:

Ů_ab2 = Ů_a2 - Ů_b2 = 81,78e^-j3°55'- 81,78e^-j123°55'=141,65e^j26°05';

Ů_bс2 = Ů_b2 – Ů_с2 = 81,78e^-j123°55'- 81,78e^-j116°05'=141,65e^-j93°55';

Ů_ac2 = Ů_c2 – Ů_a2 = 81,78e^j116°05'- 81,78e^-j3°55'=141,65e^j146°05'.

Линейные напряжения эквивалентной звезды равны фазным напря­жениям треугольника сопротивлений второго приемника (см. рис. 4.2). Фазные токи второго приемника, А: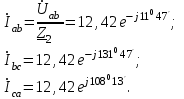



Полная мощность одной фазы второго приемника с учетом сопротивления линии электропередачи Z_Л2 равна, ВА:

S₂= U_А·I_A2= 127·21,52e^j41°48' = 2733e^j41°48' = (2037 + j1822);

Р₂= 2037 Вт; Q₂ = 1822 ВА.

4. Определим линейные и фазные напряжения и токи первого приемника, а также полную мощность одной его фазы при отключенной батарее конденсаторов.

Так как первый приемник подключен напрямую к источнику электри­ческой энергии (Z_Л = 0), то фазные и линейные напряжения приемника рав­ны фазным и линейным напряжениям генератора, В:

Ů_a1=Ů₁=127;

Ů_b1=Ů_B=127e^-j120°;

Ů_c1=Ů_C=127e^j120°;

Ů_ab=Ů_AB=220e^j30°;

Ů_bc=Ů_BC=220e^-j90°;

Ů_ca1=Ů_CA=220e^j150°;

Для приемника, соединенного в звезду, фазные токи равны линейным I_Ф=I_Л.Определяем модуль фазного тока первого приемника, А:

I_Ф=Р₂ /(3·U_Ф·cosφ₁)= 4000 /(3·127·0,7)=15

Определяем угол сдвига фаз между напряжением и током первого приемника:

cosφ₁=0,7; φ₁=45°34', (φ₁>0).

Записываем выражения фазных токов первого приемника в ком­плексной форме. Так как угол сдвига фаз между напряжением и током пер­вого приемника известен, то начальная фаза тока, например фазы А, равна

ψ_iA=ψ_UA-φ₁=0-45°34'=-45°34'

Следовательно,

İ_A1=15·e^-j45°34';

İ_B1=15·e^-j165°34';

İ_C1=15·e^-j74°26';

Полная мощность одной фазы первого приемника:

S₁= U_А·I_A1=127·15·e^j45°34'=1905 e^j45°34'=(1333+j360) BA;

P₁=1333кВт; Q₁=1360 B·A.

5. Определяем фазные (линейные) токи источника энергии при от­ключенной батарее конденсаторов (см. рис. 4.3), А:

İ'_A= İ'_A1+ İ'_A2=15·e^-j45°34'+21,52e^-j41°48'=

=10,5-j10,7+16-j14,3=26,5-j25=36,5e^-j43°21';

İ'_B=36,5e^-j163°21';

İ'_C=36,5e^-j79°39'.

6. Определяем реактивную мощность в фазе батареи конденсаторов, необходимую для повышения коэффициента мощности приемников до еди­ницы, ВА:

Q_c = Q₁+Q₂ = 1360+1822 = 3182.

7. Определяем емкостное сопротивление в фазе батареи конденсато­ров, Ом:

Q_c=I²X_c= 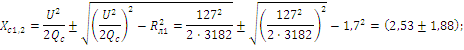·X_c= =

где Z = - модуль полного сопротивления в фазе батарея конден­саторов с учетом сопротивления линии Z_Л1=R_Л1.

;



X_c1=4,41; X_c2=0,65.

Следовательно, режиму полной компенсации реактивной мощности удовлетворяют два значения емкостного сопротивления. Принимаем боль­шее, так как, во-первых, большему сопротивлению соответствует меньший ток в фазе батареи конденсаторов и, соответственно, меньшие потери ак­тивной мощности на сопротивлении Z_Л1=R_Л1. Во-вторых, большее значе­ние емкостного сопротивления определяет меньшую емкость батареи кон­денсаторов, необходимую для компенсации реактивной мощности приемников.

8. Определяем емкость в фазе батареи конденсаторов, Ф



При этом полное сопротивление в фазе батареи конденсаторов с уче­том сопротивления линии Z_л1(рис. 4.5) равно, Ом:

Z=Z_л1-jХ_С= 1,7 - j4,41 = 4,73e^-j68°55'.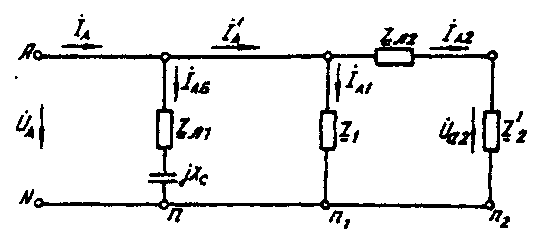



Рис. 4.5. Расчетная схема токов в фазе А с учетом батареи конденсаторов

9. Определяем фазные токи батареи конденсаторов, А: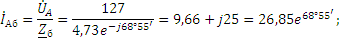



İ_Вб=26,85e ^j51°05'A; İ_Сб=26,85e^j188°55'.

10. Определяем фазные (линейные) токи источника энергии при включенной батарее конденсаторов (см. рис. 4.5), А;

İ_A=İ_Аб+I'_A=9,66+j25+26,5-j25=36,16;

İ_B=36,16e^-j120°; İ_C=36,16e^j120°.

Данные расчета показывают, что фазные токи и напряжения источни­ка совпадают по фазе. Следовательно, параметр емкости С в фазе батареи конденсаторов, необходимый для повышения коэффициента мощности приемников до единицы, выбран верно.

11. Строим векторную диаграмму токов и топографическую диа­грамму напряжений для источника и приемников электрической энергии (рис. 4.6).

На комплексной плоскости откладываем комплексные значения токов (векторы токов) и напряжений (векторы напряжений) в выбранных предва­рительно масштабах. Наиболее удобными в рассматриваемом расчете яв­ляются: масштаб напряжений т_U= 15 В/см и масштаб тока m_I=10 А/см. Векторы токов второго приемника направляем из вершин треугольника на­пряжений а, b, с . Все остальные векторы токов - из начала координат.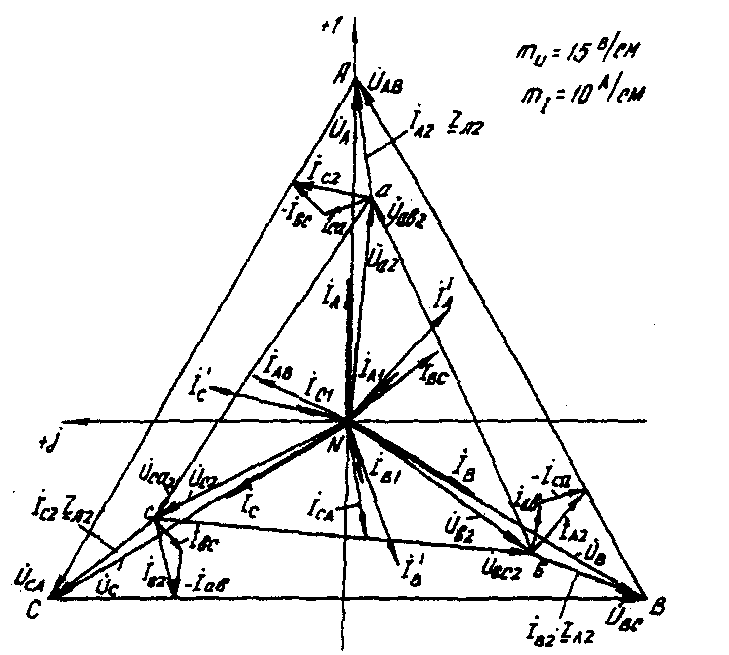



Рис. 4.6. Векторная диаграмма