Практикум по Электротехника и электроника. Задача расчет линейных электрических цепей постоянного тока
 Скачать 4.06 Mb. Скачать 4.06 Mb.
|
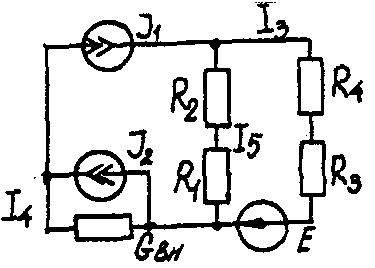
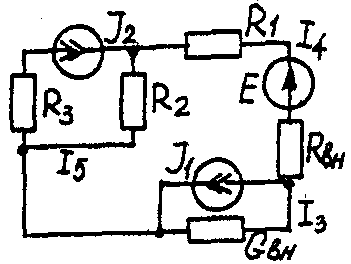
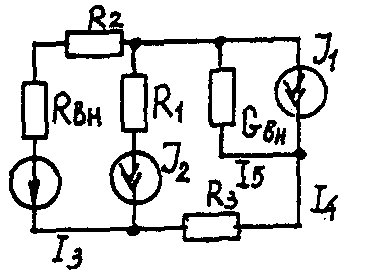
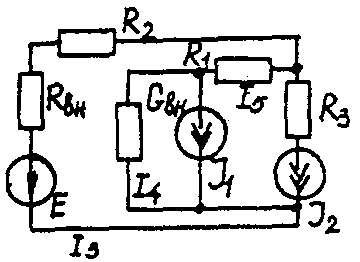
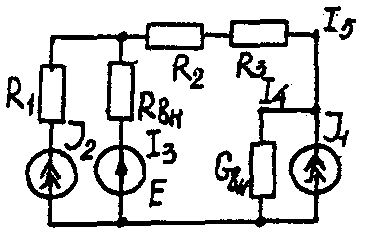
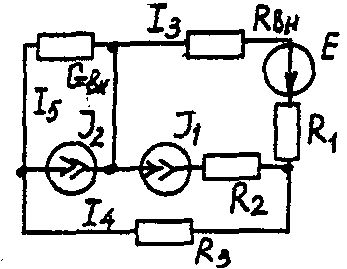
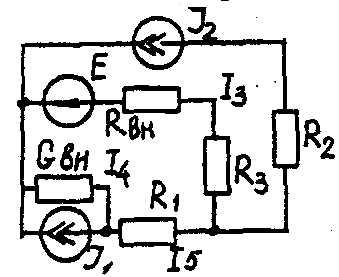
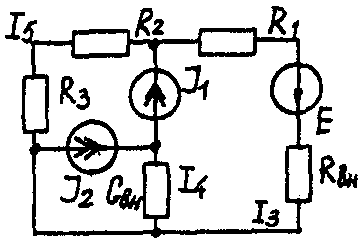
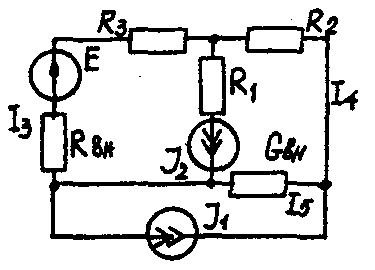
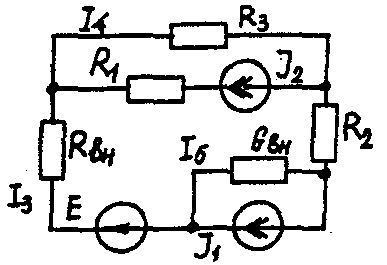
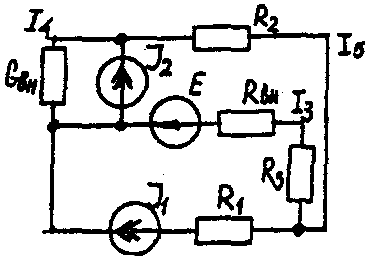
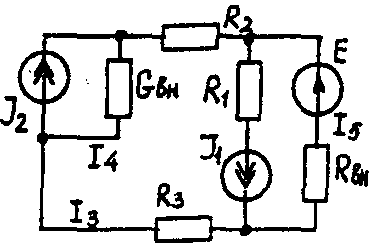
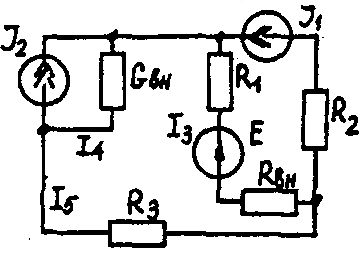
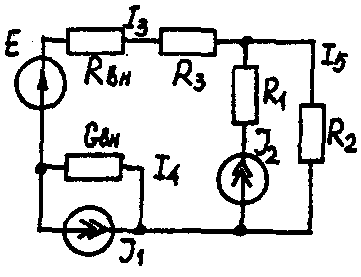
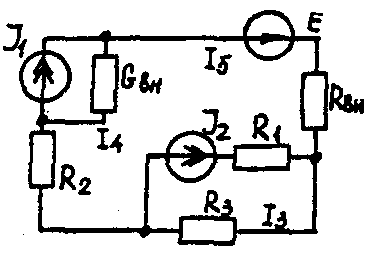
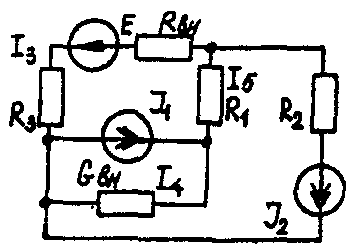
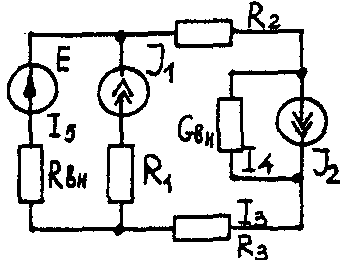
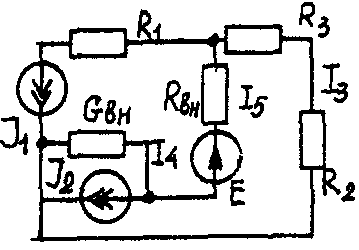
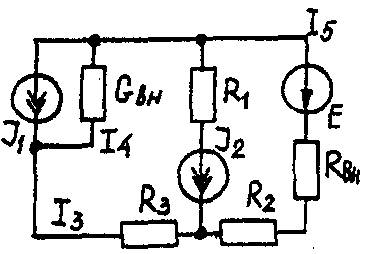
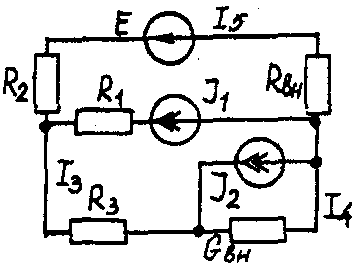
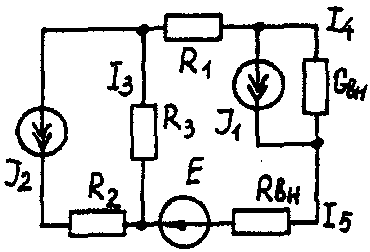
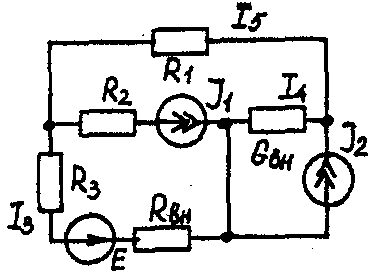
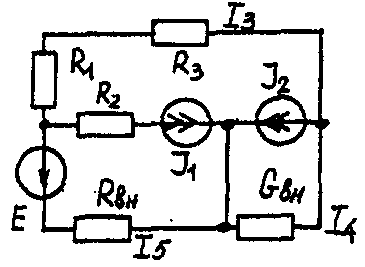
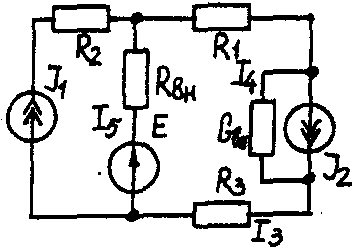
Задача 1. РАСЧЕТ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКАУсловие задачи. Для заданной электрической схемы (табл. 1.1) с известными параметрами (табл. 1.2) определить токи в ветвях цепи следующими методами: - составления уравнений электрического равновесия по законам Кирхгофа; - контурных токов; - наложения; - узловых потенциалов; - эквивалентного генератора. Метод составления уравнений электрического равновесия по законам Кирхгофа Методические указания. Этот метод основан на составлении и совместном решении системы уравнений электрического равновесия, составленных по первому и второму законам Кирхгофа. Общее число независимых уравнений (и) должно быть равно числу неизвестных токов, то есть числу ветвей электрической схемы (р) за исключением ветвей, содержащих источник тока. Последовательность решения. Выбрать условное положительное направление токов в ветвях. По первому закону Кирхгофа для схемы, содержащей (q) узлов, составить (q-1) уравнений электрического равновесия. По второму закону Кирхгофа составить [р - (q- 1)] уравнений электрического равновесия для независимых контуров. При составлении уравнений электрического равновесия следует обратить внимание на знаки. Если заданное или произвольно выбранное направление токов и э. д. с. совпадают с выбранным обходом контуров, то перед ними в уравнениях электрического равновесия ставят знак плюс, знак у падений напряжений берется в соответствии со знаком тока. Решить полученную систему уравнений электрического равновесия относительно неизвестных токов в ветвях. Выполнить проверку полученного решения по первому закону Кирхгофа для узлов заданной электрической схемы. Электрические схемы для задачи 1 Таблица 1.1.
Исходные данные для задачи Таблица 1.2
Метод контурных токов Методические указания. Этот метод заключается в представлении действительных токов в ветвях, являющихся общими для двух или большего числа смежных контуров, алгебраической суммой составляющих, каждая из которых является током, замыкающимся в одном из выбранных контуров. Эти составляющие называются контурными токами. При решении задачи этим методом в расчет вводят контурные токи, составляют уравнения электрического равновесия только на основании второго закона Кирхгофа. Вычислив контурные токи, определяют действительные токи в ветвях. Последовательность решения. Выбрать для рассматриваемой схемы независимые контуры, не содержащие источники тока (J). Задавшись положительными направлениями обхода контуров, составить для выбранных независимых контуров уравнения электрического равновесия по второму закону Кирхгофа, принимая направления контурных токов, совпадающими с выбранным обходом контуров. В уравнениях электрического равновесия учитывать и падения напряжений, обусловленные источниками тока (J) на соответствующих сопротивлениях рассматриваемого контура. Определить контурные токи. Вычислить действительные токи ветвей как алгебраические суммы токов как контурных, так и источников тока, протекающих через рассматриваемую ветвь. Метод наложения Методические указания. Этот метод основан на том, что действительный ток в рассматриваемой ветви равен алгебраической сумме составляющих токов в этой ветви, вызванных каждой из э. д. с. и источника тока в отдельности при исключении действия остальных источников э. д. с. и тока. Последовательность решения. Составить (нарисовать) электрические цепи с одним источником э. д. с. или тока, при этом зажимы остальных источников тока размыкать, а источники э. д. с. замыкать накоротко. Задаться положительными направлениями токов в ветвях. Определить составляющие - токов в ветвях, вызванных рассматриваемым источником. Определить действительные токи ветвей как алгебраическую сумму составляющих. Метод узловых потенциалов Методические указания. Этот метод заключается в определении потенциалов узлов, на основании чего вычисляются токи в ветвях по закону Ома. Потенциалы узлов определяются на основании системы уравнений электрического равновесия (1.1), составленных по первому закону Кирхгофа. При этом токи в уравнениях электрического равновесия выражают через потенциалы согласно закону Ома для участка цепи. Потенциал одного из узлов принимается равным нулю. 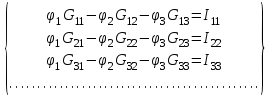 (1.1) (1.1)Где φ1, φ2, φ3, - потенциалы узлов; G11, G22, G33 - собственная (узловая) проводимость, равная сумме проводимостей всех ветвей, сходящихся в этом узле, без учета проводимостей ветвей с источниками тока; G12, G21, G31, G13, G23, G32 - взаимная проводимость, равная сумме проводимостей ветвей между двумя узлами, без учета проводимостей ветвей с источниками тока; I11, I22, I33,… - узловой ток, равный алгебраической сумме токов (J) источников тока и произведений (G-E) (э. д. с. ветвей, сходящихся в рассматриваемом узле, на их проводимости); эти величины входят в выражения узловых токов со знаком плюс, если токи (J) и э. д. с. (E) направлены к рассматриваемому узлу. Последовательность решения. Пронумеровать узлы. Потенциал одного из узлов принять равным нулю. Составить систему (q - 1) уравнений электрического равновесия (1.1) Вычислить собственные и взаимные проводимости, узловые токи и подставить в систему уравнений электрического равновесия (1.1). Определить потенциалы узлов, решив систему уравнений электрического равновесия (1.1). Определить токи ветвей по закону Ома. Ток ветви равняется разности потенциалов двух узлов, деленной на сопротивление ветви, Iветви= [ (φк – φ(к-1) ) ] /ΣRветви (1.2) Метод эквивалентного генератора Методические указания. Этот метод основан на применении теоремы об активном двухполюснике. Согласно теоремы любой активный двухполюсник, содержащий один или несколько источников энергии, можно заменить эквивалентным генератором, э. д. с. которого равна напряжению холостого хода на зажимах выделенной ветви, а внутреннее сопротивление равно входному сопротивлению двухполюсника (рис. 1.1). 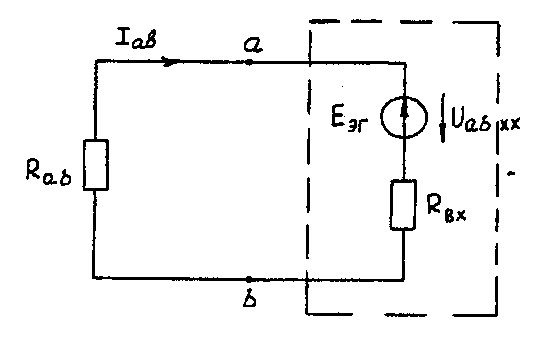 Рис. 1.1. К методу эквивалентного генератора При определении тока, например, в ветви abлюбой электрической схемы, эту схему представляют в виде двух частей: рассматриваемой ветви abи остальной части схемы - эквивалентного генератора (Еэг). Ток в ветви abопределяют по формуле: Iab = Uabxx / (Rab+Rвх) (1.3) где Uabxx - напряжение холостого хода активного двухполюсника (эквивалентного генератора) относительно зажимов рассматриваемой ветви; Rвх - входное сопротивление пассивного двухполюсника относительно зажимов ab; Rab - сопротивление рассматриваемой ветви ab. Последовательность решения. Определить напряжение Uabxxс помощью одного из известных методов расчета электрических цепей, согласно исходной схеме без рассматриваемой ветви ab. Вычислить входное сопротивление Rвхпассивного двухполюсника, т. е. сопротивление исходной электрической цепи относительно точек abбез ветви ab, при замкнутых источниках токов э. д. с. и разомкнутых источников токов. Вычислить ток в рассматриваемой ветви ab(см. рис. 1.1) по формуле (1.3). Пример решения задачи Для заданной электрической цепи (рис. 1.2) с параметрами: E=65,5 В; J1=3,5 A; J2= 8 А; R1 = 9 Ом; R2 = 7 Ом; R3 = 5 Ом; Rвн = 3 Ом; Gвн = 0,5 См, определить токи в ветвях. 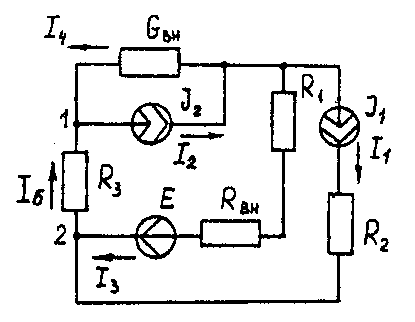 Рис. 1.2. Схема заданной электрической цепи Метод составления уравнений электрического равновесия по законам Кирхгофа В рассматриваемой электрической цепи неизвестными являются три тока (I3, I4, I5 ), для определения этих токов необходимо иметь систему из трех уравнений электрического равновесия, которые составляем по законам Кирхгофа: два уравнения электрического равновесия по первому закону Кирхгофа, предварительно задавшись положительными направлениями токов в ветвях (для узлов 1 и 2); третье уравнение электрического равновесия по второму закону Кирхгофа. Принимаем контур (R3– Gвн – R1 – Rвн - E), минуя ветви с источниками тока, и задаемся положительным направлением его обхода (см. рис. 1.2.) 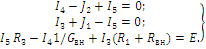 (1.4) (1.4)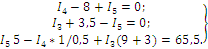 (1.5) (1.5)В результате решения системы уравнений (1.5) получим: I3 = 3 А; I4 = 1,5 А; I5 = 6,5 А. Метод контурных токов Для определения трех неизвестных токов выбираем три независимых контура (рис 1.3) и задаемся положительными направлениями их обхода, совмещая положительные направления контурных токов I11, I22, I33с направлениями их обхода I11= J1= 3,5 А ; I22 = J2 = 8 А. 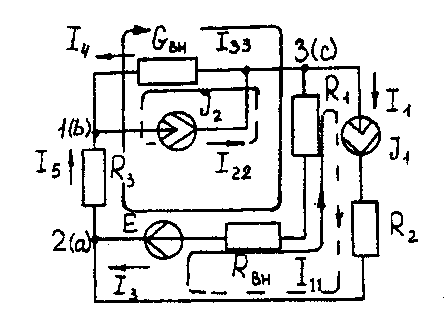 Рис. 1.3. Схема электрической цепи для метода контурных токов Таким образом, неизвестным является лишь контурный ток I33. Для третьего контура (R3 - GBH – R3 – Rвн- E) составляем уравнение электрического равновесия по второму закону Кирхгофа и определяем контурный ток I33 -I11(R1+Rвн)-I22*1/Gвн+I33(R1+Rвн+R3+1/Gвн)= Е; (1.6) -3,5(9 + 3) - 8 * 1/0,5 + I33 (9 + 3 + 5 + 1/0,5) = 65,5; отсюда I33 = 6,5 А. Действительные токи в ветвях: I3=I33-I11=6,5-3,5 = 3А; I4 = I22-I33 = 8-6,5 = l,5A, I5 = I33=6,5А. Метод узловых потенциалов Заземляем один из узлов (например 3, рис. 1.4), потенциал этого узла ( 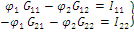 (1.7) (1.7)G11 = Gвн+ 1/R3= 0,5 + 1/5 = 0,7 См ; G12 = G21 = 1/R3 = 1/5 = 0,2 См ; G22 = 1/R3 + l/(R1 + Rвн) = 1/5 + 1/(9 + 3) = 0,28 См. I11 = -J2= - 8 A; I22= J1 + E/(R1+ Rвн) = 3,5 + 65/(9 + 3) -=9 A. 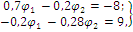 откуда φ1 = -3 В ; φ2 = 29,5 В. 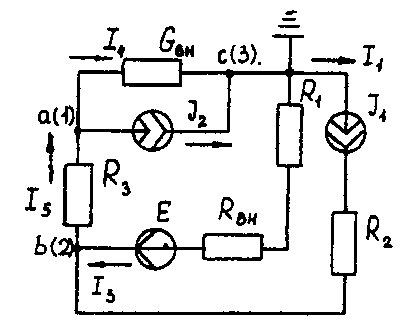 Рис. 1.4. Схема электрической цепи для метода узловых потенциалов Токи в ветвях: I3 = [(φ3- φ2) + E] * 1/ (R1 + Rвн) = [(0 - 29,5) + 65,5] * 1/(9 + 3) - 3 А; I4= (φ3 - φ1)-Gвн = (0 + 3)*0,5 = 1,5 А; I5= (φ1 – φ2) • 1/R3= (-3 - 29,5)*1/5 = -6,5 А. Знак "-" у тока I5указывает на то, что действительное направление тока противоположно выбранному. Метод наложения Определяем составляющие токов в ветвях (I`3, I`4, I`5), вызванные источником э. д. с. (E) при исключении источников тока (J1) и (J2) (рис. 1.5, а). Направление токов в цепи определяется согласно направлению источника э. д. с. (E) I`3=I`4=I`5= E/(R1+ Rвн + R3 + 1/Gвн) = 65,5/(9 + 3 + 5 + 1/0,5) = 3,45 А. Определяем составляющие токов в ветвях (I3", I4", I5"), вызванные источником тока (J1) (рис. 1.5, б) при исключении источника тока (J2) и источника, э. д. с. (Е) которого закорачивается. Направление токов в ветвях определяется согласно направлению (J1). I3"=J1(R3+ 1/Gвн)/(R1+Rвн+R3+1/Gвн)=3,5(5+2)/(9+3+5 + 2) = 1,3 А; I4" = I5" = J1– I3" = 3,5 -1,3 = 2,2 А. Определяем составляющие токов в ветвях (I3"', I4'", I5'"), вызванные источником тока (J2) (рис. 1.6, а) при исключении источника тока (J1) и источника, э. д. с. (E) которого закорачивается. Направление токов в ветвях определяется согласно направлению (J2). I3"'= I5'"=J2(1/Gвн)/(R1 + Rвн + R3+1/Gвн )= 8*2/(9 + 3 + 5 + 2) = 0,85 A; I4"'=J2- I3"'=8-0,85= 7,15A 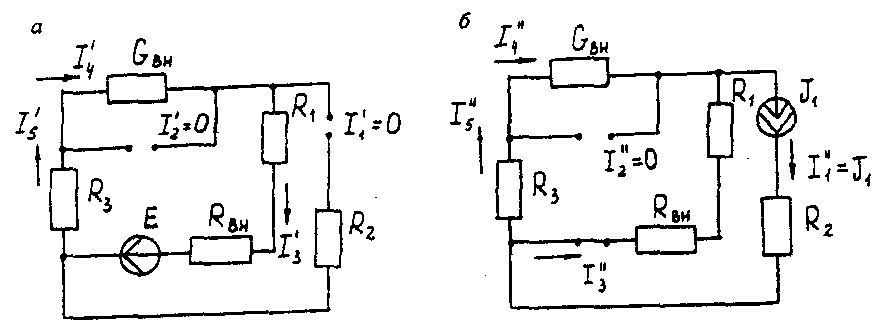 Рис. 1.5. Схема электрической цепи для метода наложения при исключении источника тока (а) и вызванные источником тока (б) 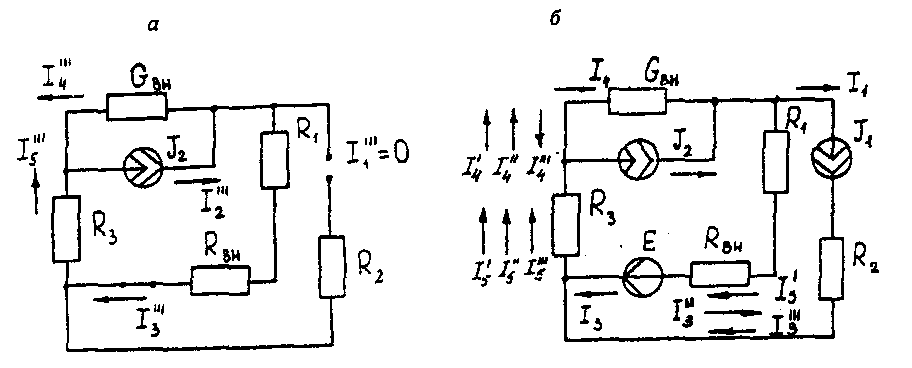 Рис. 1.6. Схема электрической цепи для определения составляющих токов в ветвях, вызванных источником тока (а) и при исключении (б) Действительные токи в ветвях определяем, как алгебраическую сумму составляющих, вызванных каждым из источников энергии (см. рис. 1.6, б): I3 = I3' - I3" + I3"'=3А; I4= - I4' - I4" + I4'"= 1,5 А; I5 =I5 ' + I5" + I5'"= 6,5 А Проверку решений выполняем, применяя первый закон Кирхгофа для трех узлов. Метод эквивалентного генератора Определить ток ветви ab. Определяем напряжение Uаbxx. При размыкании ветви abисходная схема (см. рис. 1.2) преобразуется в схему, изображенную на рис. 1.7, а. 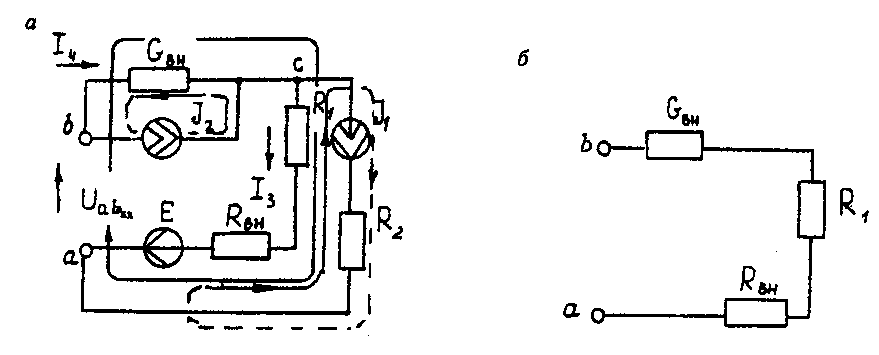 Рис. 1.7. Схема электрической цепи для метода эквивалентного генератора: а - исходная; б – преобразованная По второму закону Кирхгофа составляем уравнение электрического равновесия для контура а-b-с-а, не содержащего источников тока, обходя контур по часовой стрелке, Uаbxx-J2*1/Gвн-J1*(Rвн-R1)=E (1.8) Uаbxx - 8 -1/0,5 - 3,5 * (9 + 3) = 65,5 ; Uabxx =123,5 В. Определяем входное сопротивление относительно зажимов выделенной ветви Uаbxx, при этом зажимы источника э. д. с. закорачиваем, а зажимы источников тока размыкаем. В результате получается электрическая цепь (рис. 1.7,б) Uаbxx = 1/Gвн + R1 + Rвн=17 Ом; Iab =Uab xx(Rвх ab+ R3) = 123,5/(14 + 5) = 6,5 А. Задача 2. РАСЧЕТ ОДНОФАЗНЫХ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||