Практикум по Электротехника и электроника. Задача расчет линейных электрических цепей постоянного тока
 Скачать 4.06 Mb. Скачать 4.06 Mb.
|
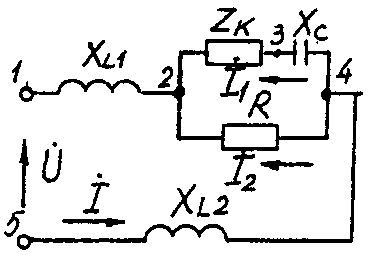
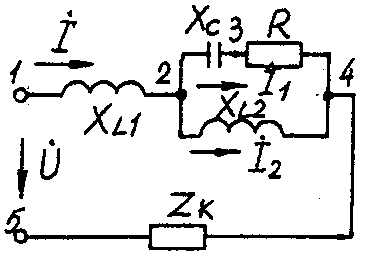
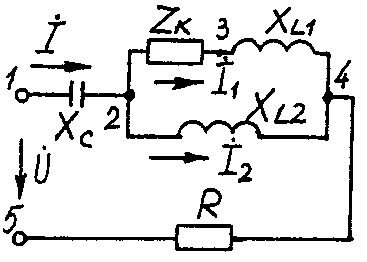
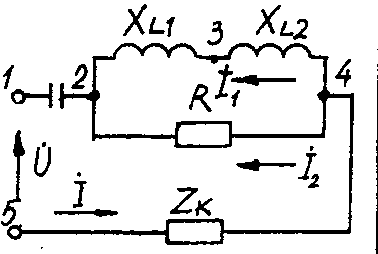
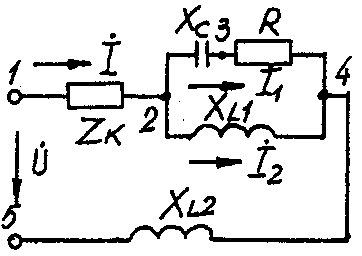
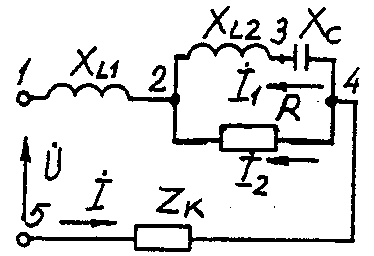
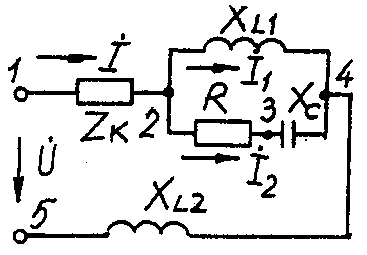
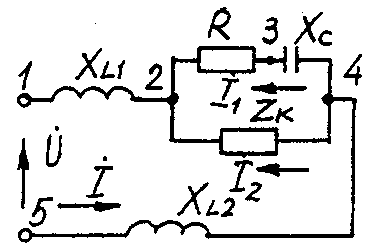
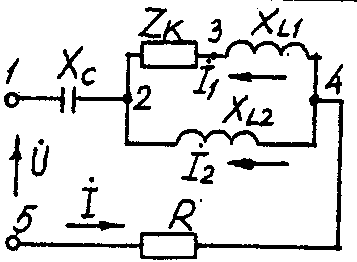
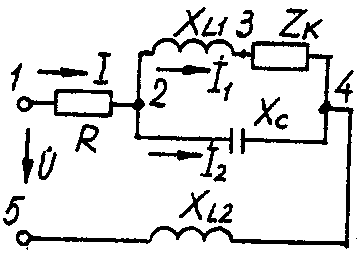
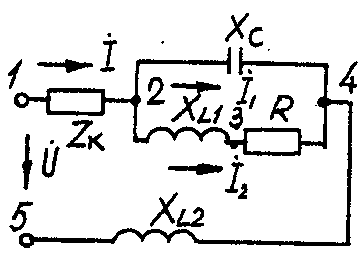
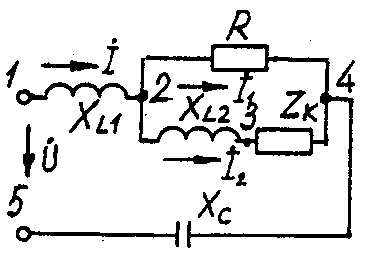
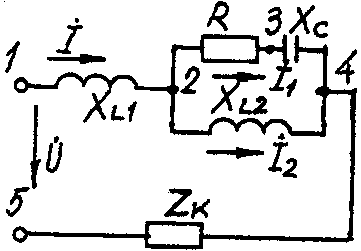
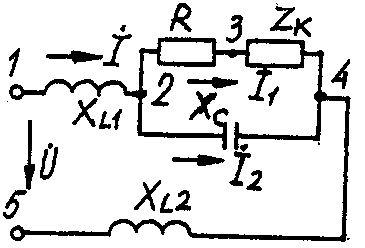
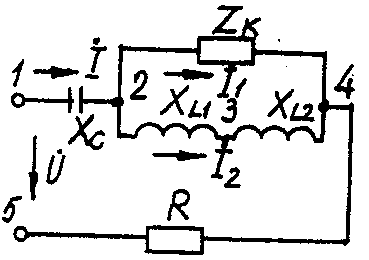
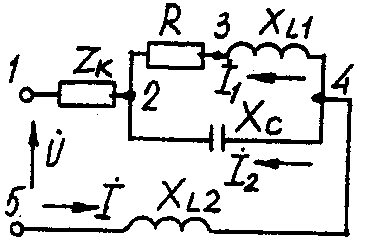
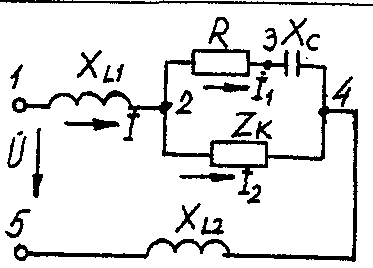
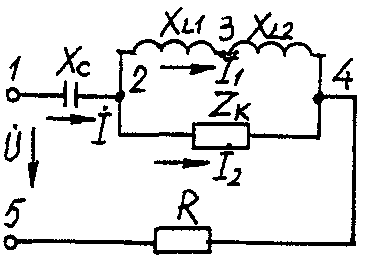
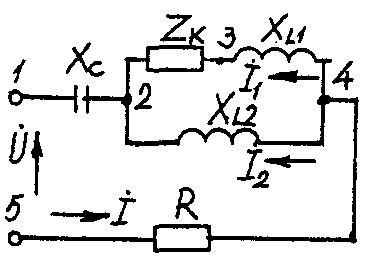
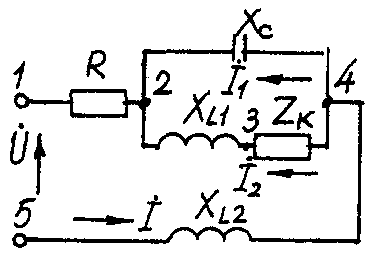
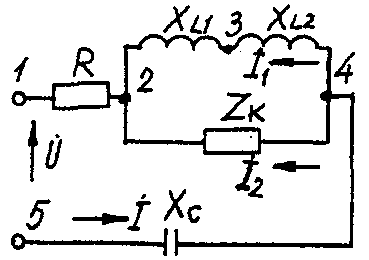
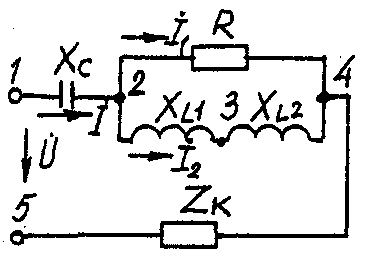
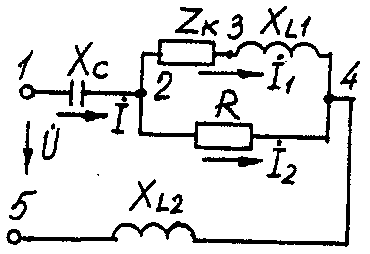
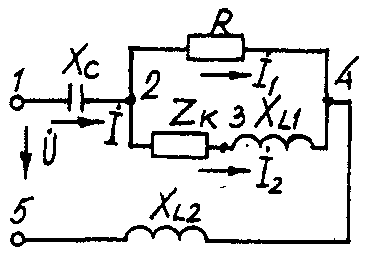
2.3. Разветвленная цепь синусоидального токаУсловие задачи. Для заданной электрической схемы (табл. 2.3) с известными параметрами (табл. 2.4) определить токи в ветвях и полный ток, напряжение на участках цепи, мощности активные, реактивные и полные отдельных ветвей и всей цепи. Построить векторную диаграмму токов и векторную топографическую диаграмму напряжений цепи. Методические указания. Решить задачу, используя символический метод расчета для действующих значений напряжений и токов. Вектор приложенного к цепи напряжения рекомендуется совместить с положительным направлением оси вещественных чисел, т. е. U=U. Заданную задачу, можно решить, используя метод составления уравнений электрического равновесия по законам Кирхгофа, метод преобразования электрической схемы или другие известные методы. Пример решения задачи Для заданной электрической цепи (рис. 2.3) с параметрами: U=100 В; Rк =6 Ом; XL1= 6 Ом; R1= 8 Ом; ХC=6 Ом; ХС=10 Ом; ХL2=11 Ом определить токи в ветвях, напряжения на участках цепи, активные, реактивные и полные мощности. Построить векторную диаграмму токов и векторную топографическую диаграмму напряжений цепи. 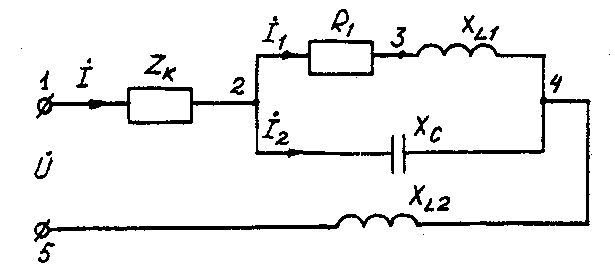 Рис. 2.3. Схема электрической цепи Задаемся условным положительным направлением токов в ветвях. Выбираем два независимых контура (1-2-3-4-5-1, 2-3-4-2). Для определения трех неизвестных токов (İ, İ1, İ2), составляем систему (2.10) из трех уравнений электрического равновесия по законам Кирхгофа (одно по первому и два по второму законам) в комплексной форме: 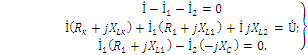 (2.10) (2.10)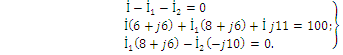 (2.11) (2.11)Электрические схемы для задачи 2.3.
Исходные данные к задаче 2.3.
Определяем токи в ветвях, решая систему уравнений (2.11), А İ1=(-1-j5,5)=5,59e-j100۫۫°, İ2=(5-j2,5)=5,59ej27۫۫°, İ=(4-j3)=5e-j37°A. Определяем падения напряжения на отдельных участках цепи, В: Ů12=İ*ZK=(4-j3)(6+j6)=(42+j6)=42,4ej8°; Ů23=İ1*R1=(-1-j5,5)8=(8-j44)=42-j100°; Ů34=İ1*jXL1=(-1-j5,5)j6=(33-j6)=33,54e-j10°; Ů24=(25-j50)=55,9e-j63°; Ů45=İ*jXL2=(4-j3)j11=(33+j44)=55e53°. Проверка решений, В: Ů = Ů 12+ Ů 23+ Ů 34+ Ů 45= 100. Определяем мощности, ВА: S12= Ů 12·Ï=42,4 ej8°·5ej37°=212ej45°=150+j150 ; S24 = Ů 24Ï1+ Ů24·Ï2=55,9e-j63°·5,59ej100°+55,9e-j63°·5,59e-j27°=313ej37°+313e-j90°=250+j188-j313; S45= Ů 45·Ï=55 ej53°·5ej37°=275ej90°=j275 ; S= S12+ S24+ S45=150+j150+250+j188-j313+j275=400+j613-j313=P+jQL - jQC. S= Ů·Ï=100 5ej37°=500ej37°=(400+j300). где Ï- сопряженные комплексы токов. Строим векторные диаграммы токов и напряжений (рис. 2.4). 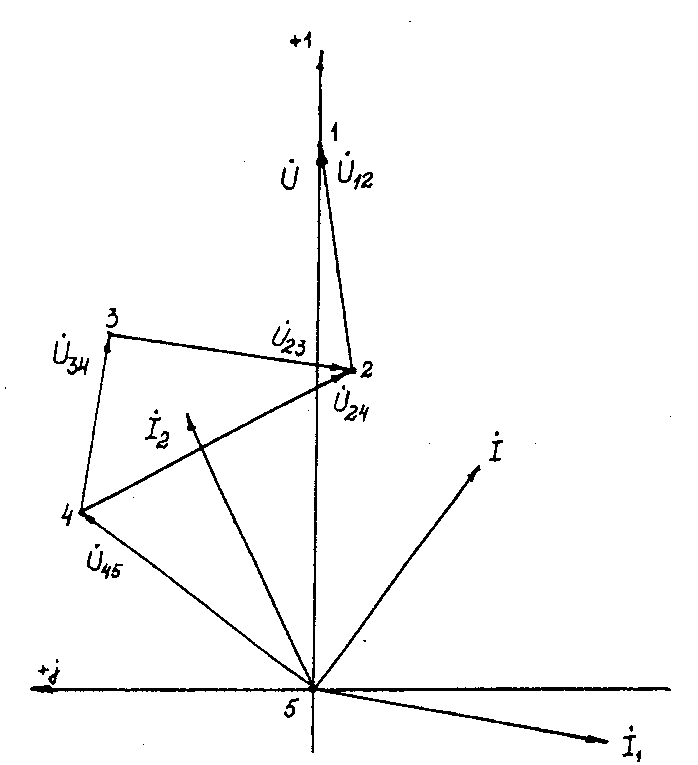 Рис. 2.4. Векторная диаграмма токов и напряжений Задача 3. РАСЧЕТ ТРЕХФАЗНЫХ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||