Практикум по Электротехника и электроника. Задача расчет линейных электрических цепей постоянного тока
 Скачать 4.06 Mb. Скачать 4.06 Mb.
|
3.1. Расчет трехфазных линейных электрических цепей при соединении фаз приемника звездойУсловие задачи. Для заданной электрической схемы (рис. 3.1) с известными параметрами (табл. 3.1) определить токи и напряжения в четырехпроводной цепи. Вычислить активную, реактивную и полную мощности цепи. Построить в масштабе векторную диаграмму линейных и фазных напряжений и токов генератора и приемника. 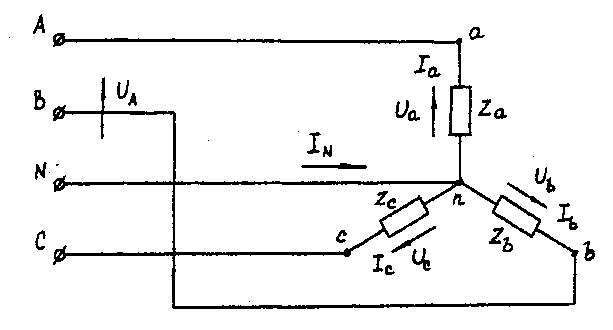 Рис. 3.1. Соединение фаз приемника звездой Определить фазные напряжения и токи после обрыва нейтрального провода. Построить векторную диаграмму линейных и фазных напряжений и токов генератора и приемника. Методические указания. Задачу решить, используя символический метод расчета. Для четырехпроводной звезды напряжения фаз генератора (источника) и приемника принять равными (т. е. пренебречь потерями в соединительных проводах). Вектор напряжения фазы "А" генератора рекомендуется совместить с положительным направлением оси вещественных чисел (ŮA= U). Трехфазную систему фазных и линейных напряжений генератора принять симметричной (т. е. напряжения равны по модулю и сдвинуты друг относительно друга на 120°). Исходные данные для задачи 3.1. Таблица 3.1
Примечание: элементы R , XL , XC в фазах соединены последовательно. Пример решения задачи Трехфазная нагрузка включена четырехпроводной звездой. Фазное напряжение генератора ŮA = 220 В; Za= 22 Ом; Zb = (16 +j12) =20ej37° Ом; Zc=(12-j16)=20e-j53° Ом. Определить токи в фазах и нейтральном проводе, мощность цепи. Построить векторную диаграмму напряжений и токов. Решение произвести для двух режимов: а) нейтральный провод исправен; б) нейтральный провод оборван. а). Нейтральный провод исправен. Ůa= ŮA=220В; Ůb= ŮB=220e-j120°=(-110-j190) B; Ůc= ŮC=220ej120(-110+j190) B. İa= Ůa/Za=220/22=10 A; İb= Ůb/Zb=220e-j120°/20ej37°=11e-j157°=(-10,13-j4,3) A; İc= Ůc/Zc=220ej120°/20e-53°=11ej173°=(-10,92+j1,34) A. İN= İa+ İb+ İc=10+(-10,13-j4,3)+(-10,92+j1,34)=(-11,05-j2,96)=11,44e-j165° A. (3.1) S(3)=Sa+ Sb+ Sc=ŮaÏa+ ŮbÏb+ ŮcÏc=220*10+220e-120°11ej157°+220ej120°11ej173°=2200+2420ej37°+2420e-j53°=2200+(1933+j1456)+(1456-j1933)=(5589-j477)=5610e-j5° BA. Векторная диаграмма напряжений и токов представлена на рис. 3.2.  Рис. 3.2. Векторная диаграмма напряжений и токов б). Нейтральный провод оборван. Четырехпроводная звезда преобразуется в трехпроводную звезду, поэтому между нейтральными точками генератора и несимметричной нагрузки появляется напряжение смещения UnN, вычисляемое по формуле: UnN=(UAYa+ UBYb + UCYc)/(Ya+ Yb + Yc). (3.2) Проводимости фаз нагрузки, См Ya =1/Za= 1/22 =0,045; Yb = 1/ Zb= 1/ 20ej37°= 0,05e-j37°=(0,04 –j0,03); Yc= 1/ Zc= 1/20e-j53°= 0,05ej53°= (0,03 +j0,04). Вычисления упрощаются, если в числителе формулы (3.2) использовать значение INиз предыдущего расчета при исправном нейтральном проводе ŮnN= (-11,05 -j2,96) / [ 0,045 + (0,04 -j0,03) + (0,03 +j0,04)] = 11,44е-j165°/0,1154ej5°=99e-j170°= (-97,5 -j17,2) В. Вычисляем напряжения фаз нагрузки, В Ůа = ŮA- ŮnN= 220-(-97,5 -j17,2) = (317,5 +j17,2)=318 еj3°; Ůb = ŮB- ŮnN=(-110 -j190)-(-97,5 -j17,2)=(-12,5 -j172,8)=173,3e-j94°; Ůc=ŮC- ŮnN= (-110+j190) - (-97,5 -j17,2)=(-12,5+j207,2)=207,4ej94°. Векторная диаграмма напряжений генератора и нагрузки представлена на рис. 3.3. 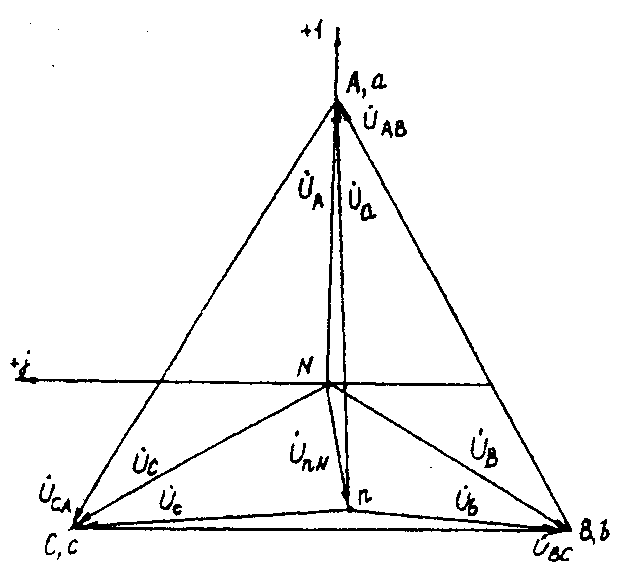 Рис. 3.3. Векторная диаграмма напряжений генератора и нагрузки 3.2. Расчет трехфазных линейных электрических цепей при соединении фаз приемника треугольником Условие задачи. Для заданной электрической схемы (рис. 3.4) с известными параметрами (табл. 3.2) определить линейные и фазные токи. Вычислить активную, реактивную и полную мощности трехфазной цепи. Построить векторную диаграмму линейных и фазных напряжений и токов генератора и приемника. 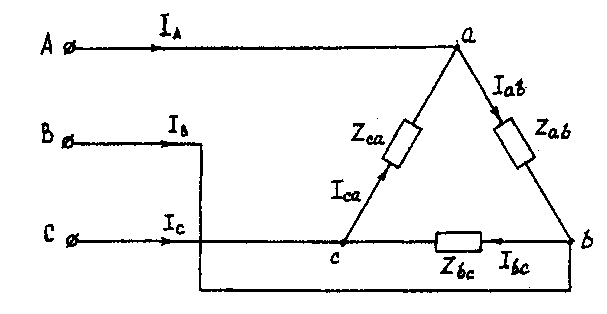 Рис. 3.4. Соединение фаз приемника треугольником Методические указания. Задачу решить, используя символический метод расчета. Фазные напряжения приемника принять равными линейным напряжениям генератора (т. е. сопротивлениями соединенных проводов пренебречь). Вектор линейного напряжения ŮABрекомендуется совместить с положительным направлением оси вещественных чисел, т. е. Ůab= ŮAB Трехфазную систему линейных и фазных напряжений генератора и приемника принять как симметричную трехфазную систему напряжений (т. е. напряжения равны по модулю и сдвинуты друг относительно друга по фазе на 120°). Последовательность решения. Начертить схему, конкретизируя нагрузку фаз приемника в соответствии с заданием. Записать комплексы фазных напряжений приемника Ůab=ŮAB=U Ůbc=ŮBC=Ue-j120° Ůca=ŮCA=Uej120° Исходные данные для задачи 3.2. Таблица 3.2
Вычислить фазные токи приемника по формулам: İab=Ůab/Zab; İbc=Ůbc/Zbc; İca=Ůca/Zca. Вычислить линейные токи по формулам: İA= İab- İca; İB= İbc- İab; İC= İca- İbc. Вычислить активную мощность цепи по формуле Р(3)= РаЬ + Рbc + Рса= Re(ŮabÏab)+Re(ŮbcÏbc)+Re(ŮcaÏca) Построить векторную диаграмму напряжений и токов. Пример решения задачи Трехфазная нагрузка соединена треугольником. Задано линейное напряжение генератора ŮAB = 380В, Zab = 22 Ом, Zbc=(16 +j12) Ом, ZCA= (16 –j12) Ом. Определить фазные и линейные токи, активную мощность цепи. Построить векторную диаграмму напряжений и токов. Записываем комплексы фазных напряжений приемника, В Ůab= ŮAB=380; Ůbc= ŮBC=380e-j120°; Ůca= ŮCA=380ej120°. Вычисляем фазные токи приемника по формулам, А: İab= Ůab/Zab=380/22=17,3; İbc= Ůbc/Zbc=380e-j120°/(16+j12)=(-17,5-j7,5)=19e-j157°; İca= Ůca/Zca=380ej120°/(16-j12)=(-17,5+j7,5)=19ej157°. Вычисляем линейные токи по формулам, А: İA= İab- İca17,3-(-17,5+j7,5)=(34,8-j7,5)=35,6e-j12°; İB= İbc- İab=(-17,5+j7,5)-17,3=(34,8-j7,5)=35,6e-j168°; İC= İca- İbc=(-17,5+j7,5)- (-17,5+j7,5)=j15. Вычисляем активную мощность цепи по формуле , Вт: Р(3)= РаЬ + Рbc + Рса= Re(ŮabÏab)+Re(ŮbcÏbc)+Re(ŮcaÏca)= =Re(380·17,3)+ +Re(380e-j120°·19ej157°)+Re(380ej120°·19e-j157°)= =6600+5776+5776=18152 Вт  Рис. 3.5. Векторная диаграмма напряжений и токов Задача 4. РАСЧЕТ СЛОЖНЫХ ТРЕХФАЗНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ Условие задачи. К зажимам симметричного трехфазного источника энергии присоединены два симметричных приемника (рис. 4.1). Первый из них соединен по схеме «звезда», потребляет активную мощность P1 при коэффициенте мощности cosφ (φ1> 0) и подключен непосредственно к зажимам источника. Второй приемник соединен по схеме "треугольник", имеет нагрузку в каждой фазе Z2и подключен к источнику энергии через линию электропередачи с сопротивлением ZЛ2. 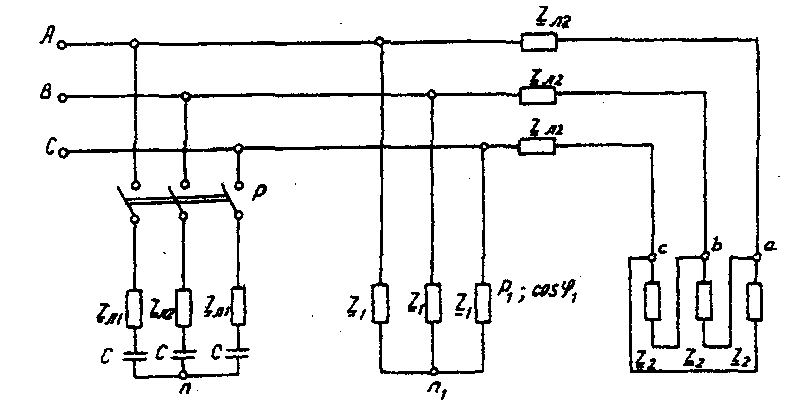 Рис. 4.1. Электрическая схема трехфазных потребителей Для повышения коэффициента мощности приемников до единицы к тому же источнику через линию электропередачи с сопротивлением ZЛ1в каждой фазе подключается батарея конденсаторов С, соединенная по схеме "звезда". Определить линейные и фазные токи и напряжения приемников при отключенной батарее конденсаторов и при включении ее; реактивную мощность в фазе батареи конденсаторов, необходимую для повышения коэффициента мощности приемников до единицы; емкость и ток в фазе батареи конденсаторов. Построить векторную топографическую диаграмму напряжений и векторную диаграмму токов источника и приемников электрической энергии. Исходные данные приведены в табл. 4.1. Исходные данные к задаче 4. Таблица 4.1
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
