Главная страница
Навигация по странице:

  • Методические указания

    		•

    Практикум по Электротехника и электроника. Задача расчет линейных электрических цепей постоянного тока


    Скачать 4.06 Mb.
    НазваниеЗадача расчет линейных электрических цепей постоянного тока
    Дата06.03.2022
    Размер4.06 Mb.
    Формат файлаdocx
    Имя файлаПрактикум по Электротехника и электроника.docx
    ТипЗадача
    #384302
    страница2 из 15
    1   2   3   4   5   6   7   8   9   ...   15

    2.1. Последовательное соединение в цепи синусоидального тока.


    На рис.2.1 представлена неразветвленная электрическая цепь.

    Исходные данные к задаче 2.1 приведены в табл. 2.1,

    Необходимо:
    1. Составить комплексное уравнение сопротивлений, построить диаграмму сопротивлений.



    2. Составить комплексное уравнение напряжений, построить векторную диаграмму напряжений. Записать полное напряжение цепи в алгебраической и показательной формах.
    3. Составить комплексное уравнение мощности, построить диаграмму мощности. Рассчитать: P, Q, S, cosφ.
    4. Записать уравнение для напряжения и тока всей цели в функции времени. На одном рисунке построить графики напряжения и тока
    Исходные данные к задаче 2.1

    Таблица 2.1

    Вариант
    R1, Ом
    R2, Ом
    L, Гн
    С, мкФ
    R3, Ом
    UR1, В
    UR3, В

    1
    8
    10
    0,0478
    636
    10
    80
    -

    2
    8
    15
    0,0318
    159
    10
    80
    -

    3
    10
    20
    0,0636
    318
    12
    100
    -

    4
    10
    25
    0,0478
    127
    12
    100
    -

    5
    12
    10
    0,0318
    159
    6
    120
    -

    6
    12
    15
    0,0636
    636
    6
    -
    60

    7
    6
    25
    0,0478
    106
    8
    -
    80

    8
    6
    10
    0,0636
    212
    8
    -
    80

    9
    8
    15
    0,0636
    79,6
    10
    -
    100

    10
    8
    20
    0,0478
    318
    10
    -
    100

    11
    10
    20
    0,096
    79,6
    12
    100
    -

    12
    10
    10
    0,0636
    318
    12
    100
    -

    13
    12
    15
    0,0636
    127
    6
    120
    -

    14
    6
    20
    0,096
    159
    6
    120
    -

    15
    6
    25
    0,0478
    159
    8
    60
    -

    16
    8
    10
    0,0318
    636
    8
    -
    80

    17
    8
    15
    0,0636
    106
    10
    -
    100

    18
    10
    20
    0,0318
    636
    10
    -
    100

    19
    10
    25
    0,0478
    79,6
    12
    -
    120

    20
    12
    10
    0,096
    212
    12
    -
    120

    21
    8
    10
    0,096
    212
    6
    80
    -

    22
    8
    15
    0,048
    636
    6
    80
    -

    23
    10
    20
    0,0636
    159
    8
    100
    -

    24
    10
    25
    0,0478
    318
    8
    100
    -



    Методические указания

    Рекомендуемая последовательность решения и расчетные формулы:

    Вычисляют индуктивное и емкостное сопротивления в цепи, Ом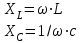

    (2.1)

    где ω — угловая частота переменного тока, ω = 314 с-1. (При вычислении ХС размерность емкости С — Ф, 1Ф = 106 мкФ).

    Вычисляют полное сопротивление цели в комплексной форме, Ом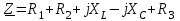

    (2.2)

    Вычисляют действующее значение тока в цепи по закону Ома, А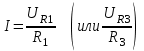

    (2.3)

    Записывают комплекс тока в цепи при начальной фазе ψi=0 как İ=I,А.

    Вычисляют напряжения на отдельных элементах цепи и всей цепи в комплексной форме, В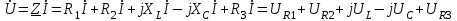

    (2.4)

    Вычисляют полную мощность цепи и мощность на элементах цепи в комплексной форме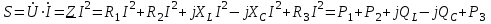

    (2.5)

    Строят (раздельно) векторную топографическую диаграмму напряжений, диаграмму сопротивлений и мощностей на комплексной плоскости в соответствии с данными вычислений по формулам (2.4), (2.2), (2.5).

    Комплексной плоскостью называется плоскость, проходящая через две взаимно-перпендикулярные оси, ось вещественных и ось мнимых чисел.

    При построении диаграммы (например, напряжений) первоначально откладывают в масштабе (m1) комплекс тока İ = I (ψ1) в положительном направлении оси вещественных чисел, затем откладывают в масштабе (mu) напряжения UR1, UR2, +jUL, UR3, -jUC. Замыкающий вектор U является вектором напряжения, приложенного к цепи. Он опережает по фазе ток при ХL > ХС (φ>0) и отстает по фазе от тока при ХL < ХС (φ<0).

    На рис.2.2,а, b, c построены, соответственно диаграмма сопротивлений, векторная топографическая диаграмма напряжений и диаграмма мощностей для произвольно принятый значений сопротивлений цепи.


    1   2   3   4   5   6   7   8   9   ...   15

    написать администратору сайта