Практикум по Электротехника и электроника. Задача расчет линейных электрических цепей постоянного тока
 Скачать 4.06 Mb. Скачать 4.06 Mb.
|
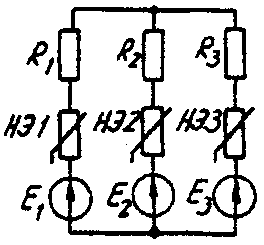
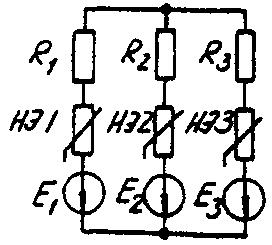
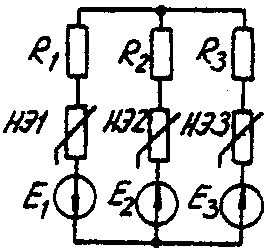
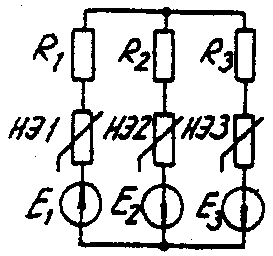
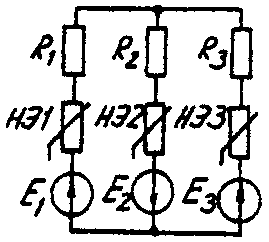
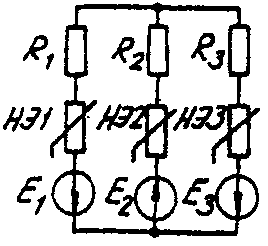
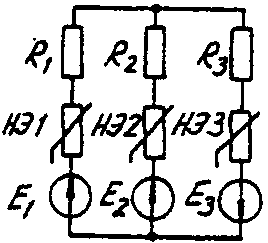
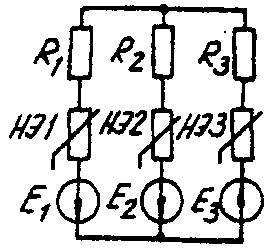
Задача 6. РАСЧЕТ НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА В УСТАНОВИВШЕМСЯ РЕЖИМЕУсловие задачи. Для заданной электрической схемы (табл. 6.1) с известными параметрами (табл. 6.2) определить токи в ветвях и напряжение на нелинейных элементах (НЭ). Вольт-амперные характеристики НЭ, симметричные относительно начала координат, приведены на рис. 6.1. 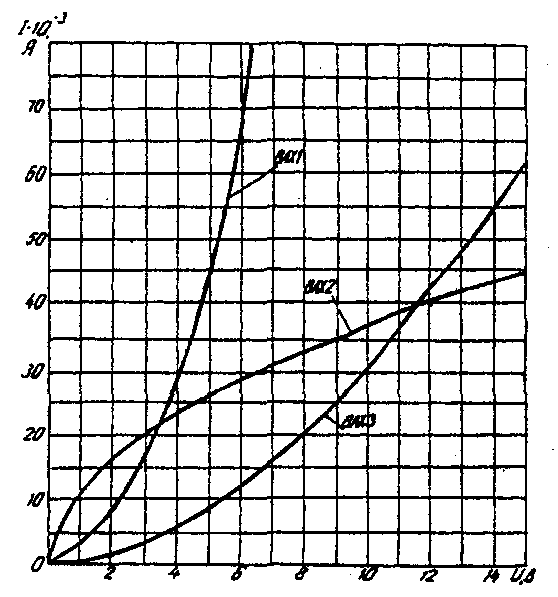 Рис. 6.1. Вольт-амперные характеристики нелинейных элементов Методические указания. Для нелинейных электрических цепей (НЭЦ) постоянного тока справедливы оба закона Кирхгофа 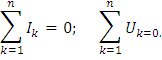 Затруднения при рассмотрении НЭЦ с помощью законов Кирхгофа заключаются в том, что в НЭЦ напряжение и токи связаны между собой нелинейными соотношениями. По этой причине для решения задач теории НЭЦ приходится использовать различные приближенные методы решения, к которым относится метод двух узлов. Расчетные электрические схемы задачи 6 Таблица 6.1
Исходные данные к задаче 6 Таблица 6.2
Расчет сложной НЭЦ, состоящей из нескольких параллельных ветвей, которые наряду с нелинейными элементами могут содержать и источники постоянной э. д. с, включенные последовательно с нелинейными элементами, сводится к нахождению токов и напряжений на участках цепи с помощью вольт-амперных характеристик. Для этого предварительно строится вольтамперная характеристика каждой ветви, которая получается смещением соответствующей характеристики НЭ на величину заданной э. д. с. влево или вправо от начала координат, в зависимости от направления э. д. с. Затем, на основании первого закона Кирхгофа, строится результирующая характеристика. Она получается смещенной относительно начала координат на величину э. д. с. (Е), которую можно рассматривать как э. д. с. эквивалентной цепи. Так как сумма токов в узле равна нулю, то в эквивалентной цепи ток отсутствует. Следовательно, значение э. д. с. (Е) равно разности потенциалов верхнего узла относительно нижнего узла исходной схемы. Отсюда находят напряжение в каждом НЭ UНэк=Eк-E Ток в каждом НЭ определяется по соответствующей вольт-амперной характеристике. Последовательность решения задачи. 1. Задаться положительным направлением токов в ветвях схемы. 2. На основании второго закона Кирхгофа построить эквивалентные вольт-амперные характеристики для ветвей. 3. На основании первого закона Кирхгофа построить результирующую вольт-амперную характеристику всей электрической цепи. 4. По результирующей вольт-амперной характеристике определить напряжения на каждом НЭ и токи в каждой ветви по соответствующим вольт-амперным характеристикам. Пример решения задачи. Для заданной электрической схемы (рис. 6.2, а) с известными параметрами Е1 =12 В, Е2= 10 В, E3= 3 В, R1=200 Ом, НЭ1, НЭ2 и НЭ3 (вольт-амперные характеристики которых приведены на рис. 6.3) определить токи в ветвях и напряжения на НЭ. 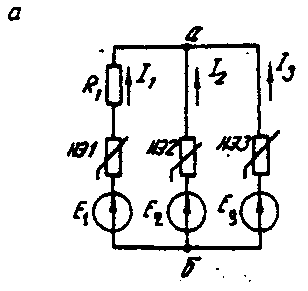 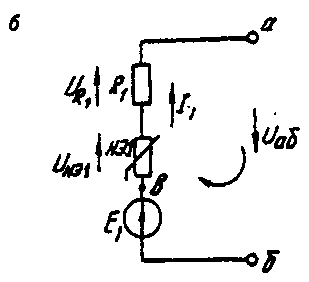 Рис. 6.2. Заданная (а) и расчетная (б) электрические схемы 1. Задаемся положительным направлением токов во всех ветвях цепи. 2. Так как каждый из токов является нелинейной функцией падения напряжения на своем НЭ, необходимо выразить его в функции одного переменного напряжения Uаб между узлами а и б. Рассмотрим первую ветвь, содержащую последовательно соединенные резистор R1, НЭ1 и источник постоянной э. д. с. Е1(рис. 6,2, б). На основании второго закона Кирхгофа для контура, указанного на рис. 6.2, б круговой стрелкой, запишем Е1=Uаб+UR1+UНЭ1 или Uаб=E1-( UR1+ UНЭ1). Если э.д.с. (Е1) действует в направлении выбранного положительного тока, т. е. Е1> 0, то при положительном токе она способствует прохождению тока и при Е1< Uаб уменьшает значение. На рис. 6.4 изображены характеристики первого нелинейного элемента I1 =f(UНЭ1), резистораI1=f(UR1), суммарная I1 =f(Uаб ) и прямая, соответствующая Е1 > 0. Здесь же нанесена результирующая характеристика I1 =f(Uаб ). 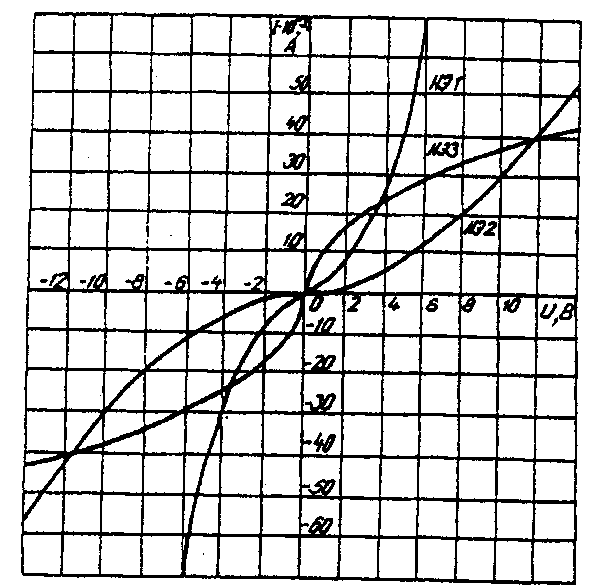 Рис. 6.3. Вольт-амперные характеристики нелинейных элементов 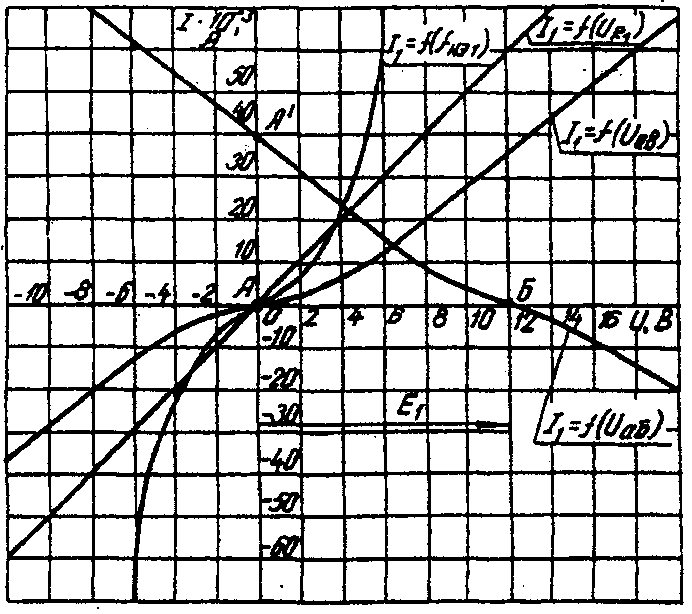 Рис. 6.4. Вольт-амперные характеристики первого нелинейного элемента 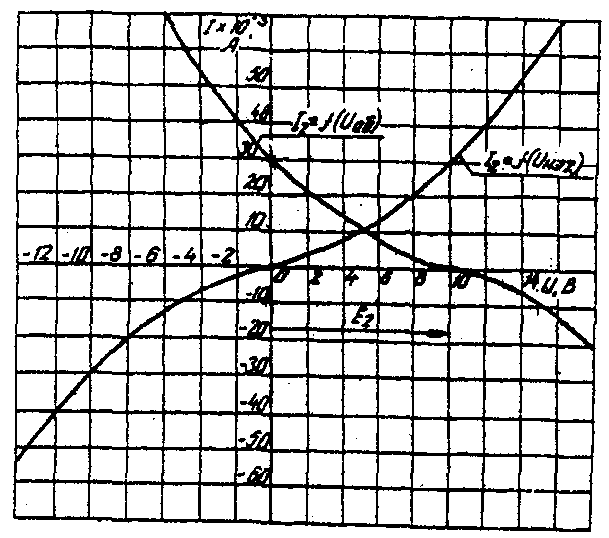 Рис. 6.5. Вольт-амперные характеристики второго нелинейного элемента Для т. А кривой I1=f(UНЭ1) напряжение на первом нелинейном элементе будет равно нулю (UНЭ1= 0) при I1=0. При этом Uаб = E1т. е. начало) кривой I1=f(Uаб) сдвинуто в точку Б, в которой Uаб = E1. Росту Uаб , при Uаб >0 соответствует уменьшение Uаб. Для точки A' при Uаб = E1, Uаб = 0. Росту Uаб при Uаб < 0 отвечает увеличение Uаб, причем Uаб > E1. Аналогичным образом перестраивают кривые I2=f(UНЭ2) и I3 =f(Uнэз) для других ветвей схемы (рис. 6.5 и 6.6). 3. Нанесем кривые I1=f(Uаб), I2=f(Uаб) и I3 =f(Uаб) на одном рисунке и построим результирующую вольт-амперную характеристику I=f(Uаб)просуммировав ординаты кривых (рис. 6.7). 4. Точка А пересечения кривой I=f(Uаб) с осью абсцисс дает значение Саб, при котором удовлетворяется уравнение I1 + I2 + I3 = 0. Восстанавливаем в этой точке перпендикуляр к оси абсцисс до пересечения с кривыми I1=f(Uаб), I2=f(Uаб) и I3 =f(Uаб) и находим токи I1, I2 и I3как по величине, так и по знаку. 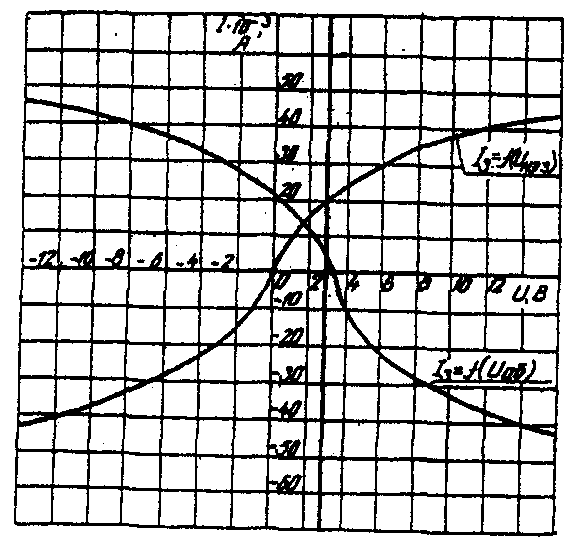 Рис 6.6. Вольт-амперные характеристики третьего нелинейного элемента Сделаем проверку I1 + I2 + I3=15·10-3+5·10-3-20·10-3=0 A. 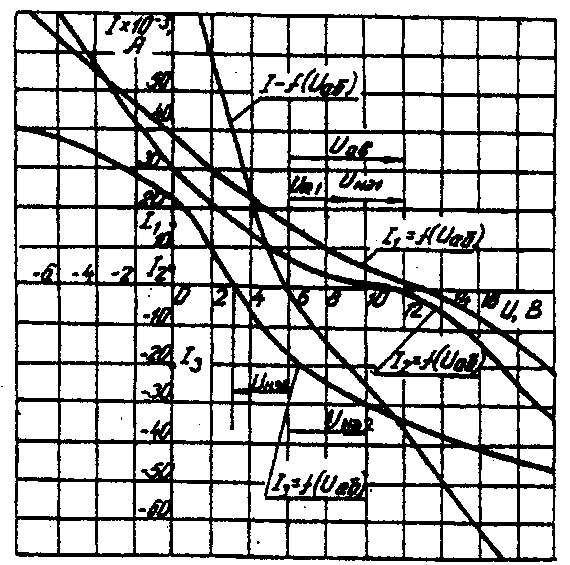 Рис. 6.7. Результирующие вольт-амперные характеристики Для рассматриваемого примера имеем (см. рис. 6.7), А I1=15·10-3; I2=5·10-3; I3=-20·10-3.w Располагая построенными характеристиками, легко находим напряжения на всех нелинейных элементах цепи (см. рис. 6.7): UНЭ1 = 3; UНЭ2 = 2; UНЭ3 = 3. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||