Практикум по Электротехника и электроника. Задача расчет линейных электрических цепей постоянного тока
 Скачать 4.06 Mb. Скачать 4.06 Mb.
|
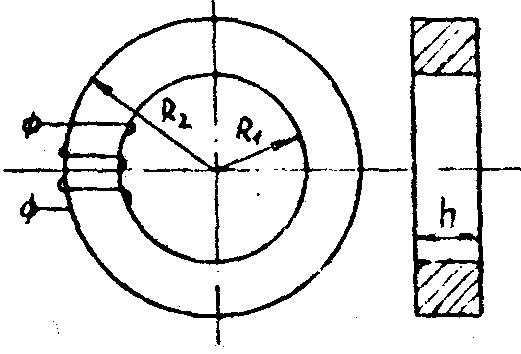
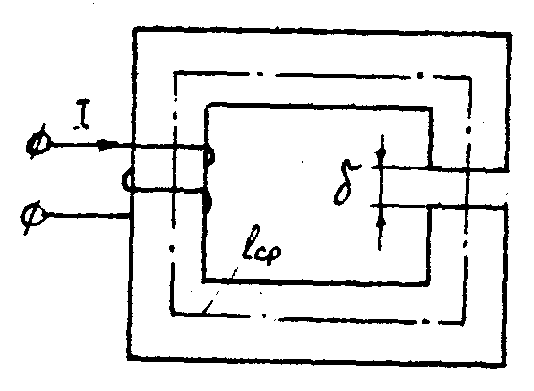
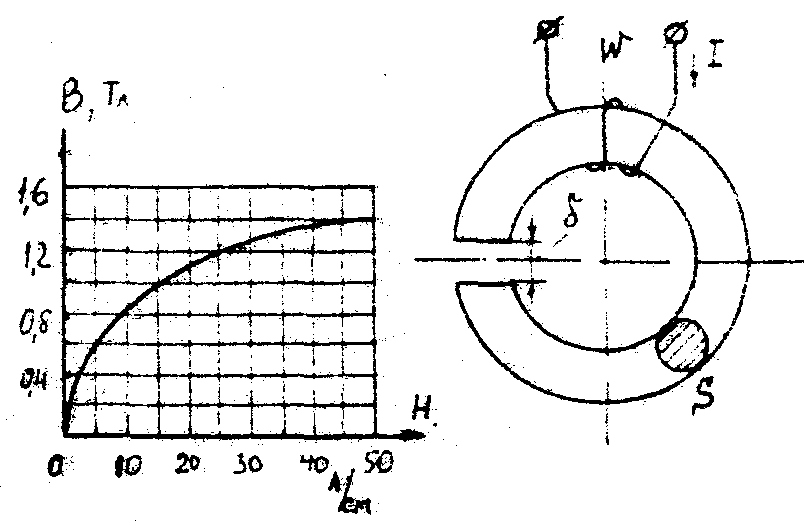
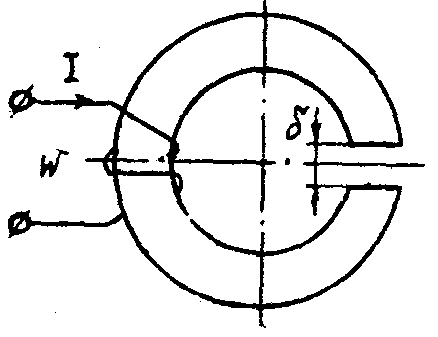
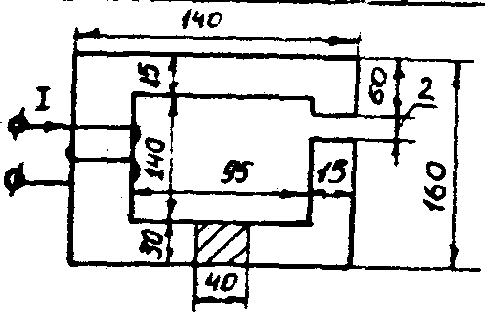
7.1.1. Прямая задача. Определить МДС цепи по заданному магнитному потоку.Порядок расчета следующий: 1. Магнитная цепь разбивается на участки, имеющие одинаковое сечение и одинаковую магнитную проницаемость; 2. По известным геометрическим размерам магнитного сердечника определяются длины l и площади поперечного сечения выделенных участков; 3. Исходя из постоянства магнитного потока вдоль всей цепи определяются значения магнитной индукции для выделенных участков магнитной цепи по заданному магнитному потоку; 4. По заданной кривой намагничивания определяются значения напряженности магнитного поля для известных значений магнитной индукции. Напряженность поля и воздушном зазоре определяется по формуле: H5 =0,8 • 106 В5 5. подсчитывается сумма падений магнитного напряжения вдоль всей магнитной цепи ΣHKlK и на основании закона полного тока приравнивается эта сумма полному току IW или МДС. 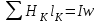 Пример. Геометрические размеры магнитной цепи даны на рис. 7.2. Найти какой ток должен протекать по обмотке с числом витков w=500 чтобы магнитная индукция в воздушном зазоре Вδ=1 Тл. Решение. Магнитную цепь рис. 7.1 разбиваем на три участка: 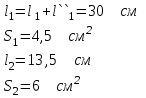 Воздушный зазор 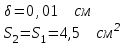 Индукция 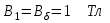 Индукцию на участке l2 найдем, разделив поток Ф = ВδSδ на сечение S2 второго участка 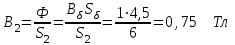 Напряженности поля на первом и втором участках определяем согласно кривой намагничивания (рис. 4) по известным значениям В1 и В2; Н1 = 300 А/м; Н2 = 115 А/м Напряженность поля в воздушном зазоре Нδ = 0,8·106·Вδ = 0,8·106·1 = 8·105 А/м Определяем падение магнитного напряжения вдоль всей магнитной цепи: 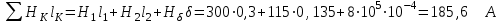 Ток в обмотке 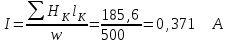 Задания к задаче 7.1.1 и 7.1.2
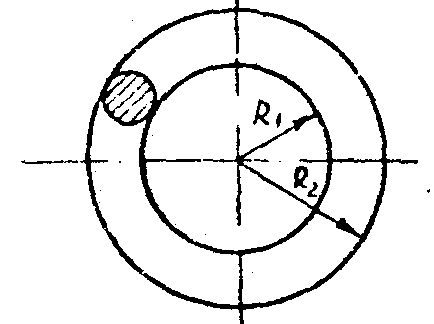
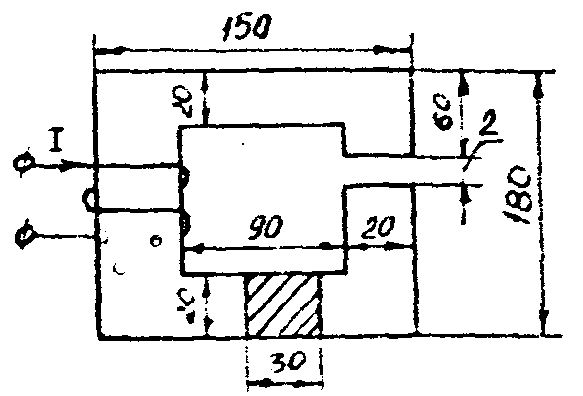
7.1.2. Обратная задача. Определить магнитный поток в цепи по заданной МДС Условие задачи: Для заданной магнитной цепи (рис. 7.2.) с известными параметрами (таб. 7.2.). Найти магнитные потоки в магнитной цепи. Примечание – геометрические размеры даны в мм, кривая намагничивания дана на рис. 7.4. Порядок решения обратной задачи следующий: 1) магнитная цепь разбивается на участки с одинаковыми сечением и магнитной проницаемостью. Определяются длины и сечения этих участков; 2) строится вебер-амперная характеристика 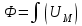 цепи; цепи;3) пользуясь вебер-амперной характеристикой, по заданной‚ МДС определяют магнитный поток Ф. Результаты расчетов для построения 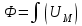
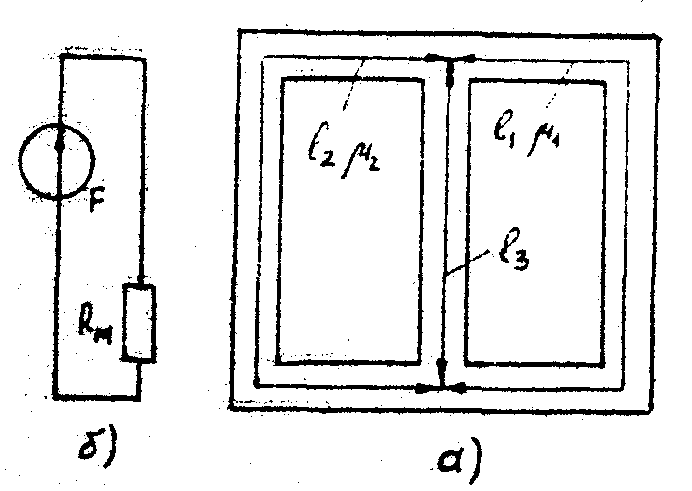
Пример. Найти магнитную индукцию в воздушном зазоре магнитной цепи (рис. 7.1), если Iw = 350 А. (см рис. 7.2.) Решение. Строим вебер-амперную характеристику. Для этого задаемся значениями Вδ; равными 0,5; 1,1; 1,2 и 1,3 Тл, и для каждого из них определяем параметры, указанные в табл. 1. Так же, как и в предыдущей задаче определяем 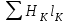 По данным табл. 7.2 строим вебер-амперную характеристику 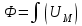 (рис. 7.5) и по ней определяем, что при Iw = 350 А (рис. 7.5) и по ней определяем, что при Iw = 350 АФ = 55·10-5 Вб Следовательно, 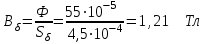 7.2 Разветвленная магнитная цепь Исходные данные к расчету разветвленной магнитной цепи приведены в табл 7.4 Расчет разветвленной магнитной цепи аналогичен соответствующей электрической с сосредоточенными параметрами. Так как магнитные цепи являются нелинейными, то методы их расчета при этих условиях аналогичны методам расчета нелинейных электрических цепей. Все методы расчета электрических цепей с нелинейными сопротивлениями полностью применимы к расчету магнитных цепей, так как магнитные и электрические цепи подчиняются одним и тем же законам – законам Кирхгофа.  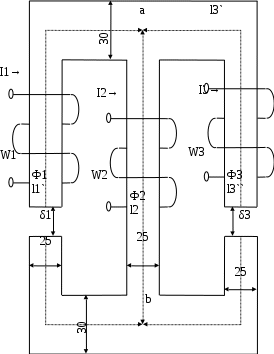 Рис. 7.4 Разветвленная магнитная цепь Задание к задаче 7.2
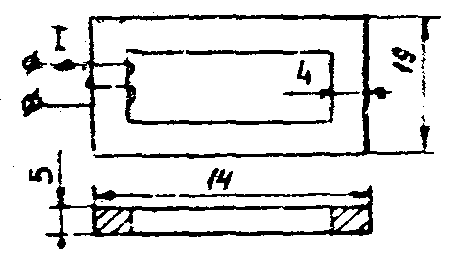
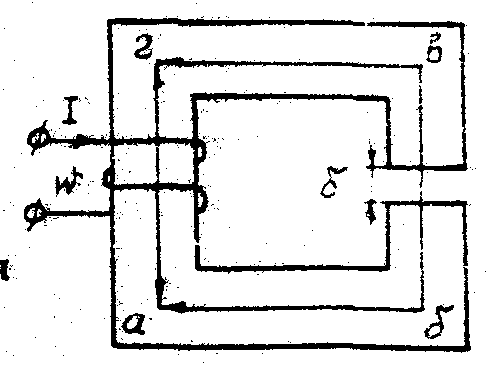
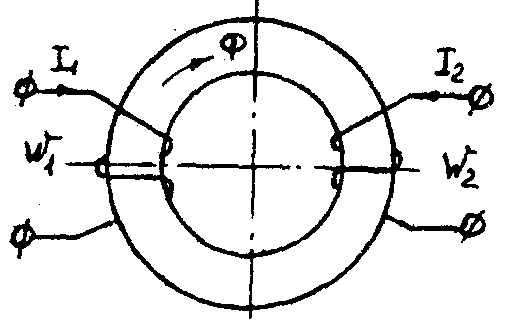
В качестве примера рассмотрим расчет разветвленной цепи методом двух узлов. Найти магнитные потоки в ветвях магнитной цепи (рис. 7.2). Геометрические размеры даны в мм. Кривая намагничивания представлена на рис. 4. I1w1 = 80 А; I2w2 =300 А; зазоры δ1 = 0,05 мм и δ2 = 0,22 мм. Решение. Составам электрическую схему замещения магнитной цепи (рис. 7.6). Узловые точки обозначим буквами «а» и «b».  Определим длины участков магнитной цепи 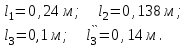 Длинам l3` и l3`` участки третьей ветви, имеющей площади сечения 9 и 7,5 см2. Выберем положительные направления магнитных потоков Ф1, Ф2 и Ф3 к узлу «а». Построим зависимость потока от падения магнитного напряжения первой ветви UМ1. Для этого произвольно задаемся рядом числовых значений Ф1, для каждого значения находим индукцию В1 и по кривой намагничивания — напряженность Н1 на пути в стали по первой ветви. Магнитное напряжение на первом участке 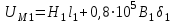 Таким образом, для каждого значения потока Ф1 подсчитываем UМ1 и по точкам строим зависимость 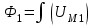 (кривая 1 рис. 7.7). Аналогично строим зависимость (кривая 1 рис. 7.7). Аналогично строим зависимость 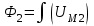 (кривая 2 рис. 7.7) (кривая 2 рис. 7.7)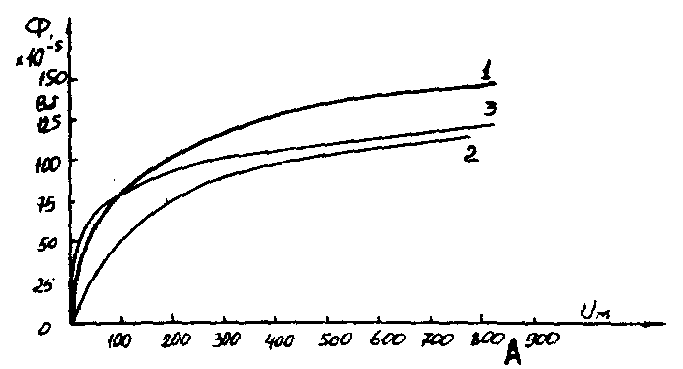 Рис. 7.7. Вебер-амперные характеристики ветвей Кривая 3 (рис. 7.7) есть зависимость 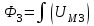 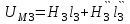 Для определения потоков Ф1, Ф2 и Ф3 постройте зависимости этих потоков от магнитного падения напряжения UMab между узлами «а» и «b» (рис. 7.6). Запишем уравнение по второму закону Кирхгофа для первой ветви: 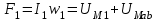 отсюда 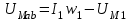 Согласно выражению приведенному выше строим зависимость 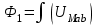 (рис. 7.8). Для этого кривую 1 (рис. 7.7) при переносе на рис.7.8 смещаем вправо на величину I1w1 и, так как перед UM1 стоит знак “-“, зеркально отобразим относительно вертикальной оси. (рис. 7.8). Для этого кривую 1 (рис. 7.7) при переносе на рис.7.8 смещаем вправо на величину I1w1 и, так как перед UM1 стоит знак “-“, зеркально отобразим относительно вертикальной оси.Запишем уравнение по второму закону Кирхгофа для второй ветви 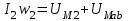 отсюда 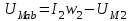 Построим зависимость 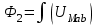 (рис. 7.8). Для этого кривую 2 (рис. 7.7) смещаем вправо от начала координат на величину I2w2 и зеркально отобразим относительно вертикальной оси. (рис. 7.8). Для этого кривую 2 (рис. 7.7) смещаем вправо от начала координат на величину I2w2 и зеркально отобразим относительно вертикальной оси.В аналогичном порядке строим зависимость 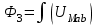 (рис. 7.8) (рис. 7.8)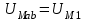  3ависимость 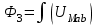 так же, как и кривая 3 (рис. 7.7) проходит через начало координат. так же, как и кривая 3 (рис. 7.7) проходит через начало координат.Построим кривую 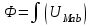 (рис. 7.8), где (рис. 7.8), где 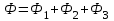 Точка (m) пересечения кривой 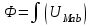 с осью абсцисс дает значение UMab, удовлетворяющее первому закону Кирхгофа с осью абсцисс дает значение UMab, удовлетворяющее первому закону Кирхгофа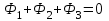 Восстановим в этой точке перпендикуляр к оси абсцисс. Ординаты пересечения перпендикуляра с кривыми дадут значения магнитных потоков в ветвях; Ф1 = 126,2·10-5 Вб; Ф2 = -25·10-5 Вб; Ф3 = -101,2·10-5 Вб. В результате расчета потоки Ф2 и Ф3, оказались отрицательными. Это означает, что в действительности они направлены противоположно выбранным ранее для них направлениям, показанным на рис. 7.2 и рис. 7.6. Задача 8. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ Условие задачи. Для заданной электрической схемы (табл. 7.1) по известным параметрам 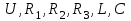 (табл. 7.2) и характеристике нелинейного элемента (рис. 7.1, 7.2, 7.3) построить динамическую кривую тока переходного процесса. (табл. 7.2) и характеристике нелинейного элемента (рис. 7.1, 7.2, 7.3) построить динамическую кривую тока переходного процесса.Задачу решить следующими методами: Последовательных приближений, Кусочно-линейной аппроксимации. Аналитической аппроксимации. Графического интегрирования 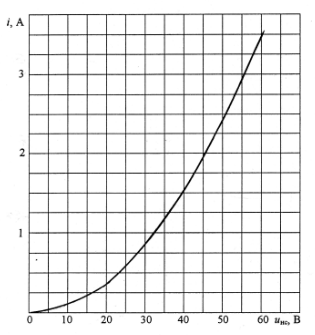 Рис. 8.1 Вольт-амперная характеристика (В.А.Х.) нелинейного сопротивления 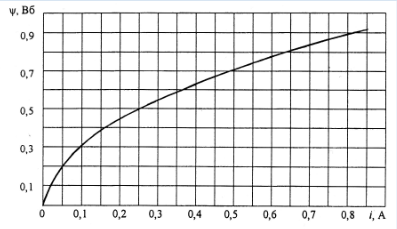 Рис. 8.2. Вебер-амперная характеристика (Вб. А. Х.) нелинейной индуктивности 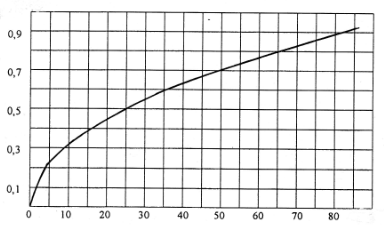 Рис. 8.3. Кулон-вольтная характеристика (К. В. Х.) нелинейного конденсатора Таблица 8.1 Электрические схемы для задачи 8 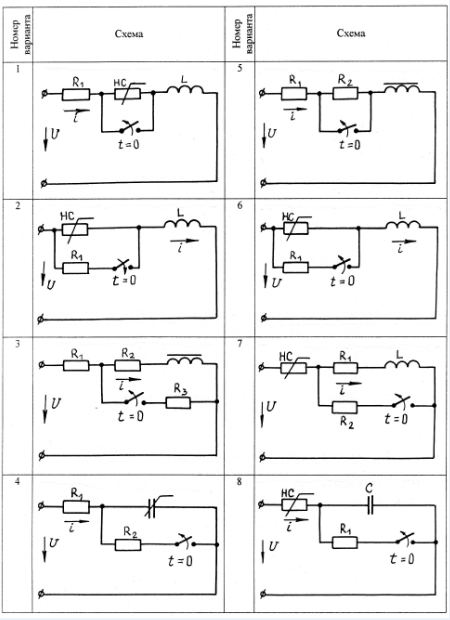 Продолжение табл. 8.1 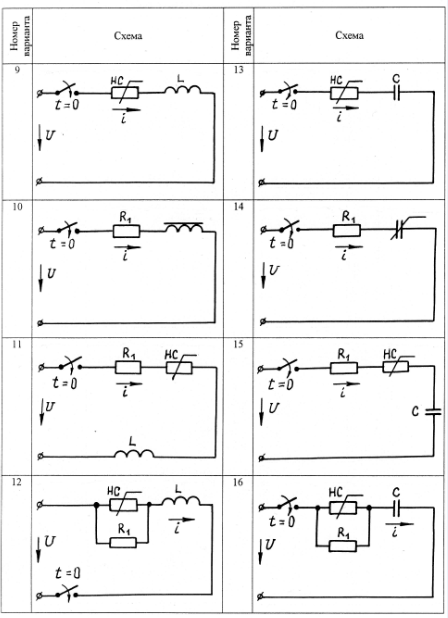 Окончание табл. 8.1 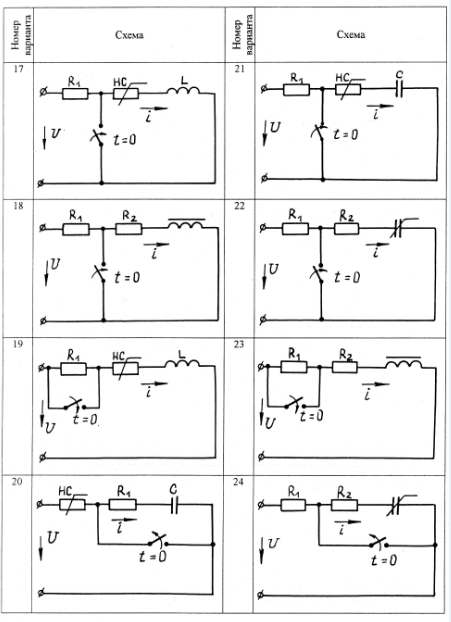 Таблица 8.2 Исходные данные для задачи 8
Переходные процессы в нелинейных цепях описываются нелинейными дифференциальными уравнениями, для которых не существует общего аналитического решения. В зависимости от конкретных условий решаемой задачи выбирается тот или иной метод расчета. Трудности, с которым сопряжен расчет, возрастают по мере усложнения схем и характера воздействующих функций. На практике нашли применение приближенные методы расчета - аналитические и графо-анапитичиские. Аналитические методы расчета заключаются в приближенном интегрировании нелинейных дифференци- альных уравнений, когда нелинейные характеристики аппроксимируются аналитическими функциями. Графо-аналитические методы расчета не требуют аналитической аппроксимации характеристик. Решение находится графическим построением, которое сопровождается дополнительными аналитическими вычислениями. В связи с широким развитием и применением вычислительной техники, анализ переходных процессов в нелинейных цепях существенно облегчен использованием аналоговых и цифровых вычислительных машин. Ниже рассмотрены эти методы, нашедшие практическое применение при расчете переходных процессов в нелинейных электрических цепях. Метод последовательных приближений Являясь графо-аналитическим и отличаясь простотой, данный метод применяется, в основном, для ориентировочных расчетов. Суть метода состоит в том, что в первом приближении характеристика нелинейного элемента заменяется прямой линией. Эта линия проходит через начало координат или точку, которая соответствует значению искомой функции при t = 0 (в момент коммутации) и точку установившегося режима. Таким образом, в первом приближении задача сводится к решению линейного дифференциального уравнения. Далее, с учетом нелинейности заданной характеристики нелинейного элемента, путем графического построения производят уточнение кривой первого приближения. При этом необходимо осуществить операцию графического интегрирования или дифференцирования промежуточной функции, выражение которой получают из исходного нелинейного дифференциального уравнения, составленного для электрической цепи послекоммутационного режима. Процесс приближения повторяют до тех пор, пока в решении не по- лучится одна и та же динамическая кривая. Обычно для практических расчетов достаточно двух, трех приближений. В качестве примера рассмотрим процесс включения электрической цепи (рис. 8.4, а),состоящей из последовательно соединенных индуктивности Lи нелинейного активного сопротивления НС, характеристика которого ит=f[i)задана графически (рис. 8.4, б), на постоянную э. д. с. (Е). 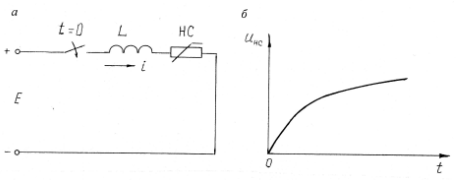 Рис. 8.4. Схема включения электрической цепи с элементами Lи НС (а) и вольт-амперная характеристика НС (б) Составим дифференциальное уравнение для электрической цепи послекоммутационного режима (уравнение по 2-му закону Кирхгофа) 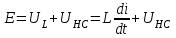 Полученное уравнение является нелинейным, поскольку связь между током iи напряжением на нелинейном сопротивлении иНСопределяется нелинейной функцией (см. рис. 8.4, б). Для определения переходного тока i(t)первого приближения осуществим замену нелинейной функции В. А. X. прямой, проходящей через точку «а» установившегося режима и начало координат (рис. 8.5). 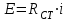 где, 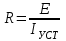 - статическое сопротивление, соответствующее току установившегося режима - статическое сопротивление, соответствующее току установившегося режима  Падение напряжения на индуктивности в установившемся режиме равно нулю uL=L 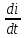 = 0 и все напряжение источника э. д. с. будет приложено к нелинейному сопротивлению инс = Е. Таким образом, ток установившегося режима = 0 и все напряжение источника э. д. с. будет приложено к нелинейному сопротивлению инс = Е. Таким образом, ток установившегося режима  можно определить по графику, откладывая э. д. с. (Е)на В. А. X. нелинейного сопротивления (см. рис. 8.5). можно определить по графику, откладывая э. д. с. (Е)на В. А. X. нелинейного сопротивления (см. рис. 8.5).Если уравнение прямой 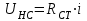 подставить в нелинейное дифференциальное уравнение, то оно вырождается в линейное и, следовательно, появляется возможность его аналитического решения подставить в нелинейное дифференциальное уравнение, то оно вырождается в линейное и, следовательно, появляется возможность его аналитического решения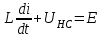 Задачи подобного класса были рассмотрены при анализе переходных процессов в линейных электрических цепях (подключение реальной катушки к источнику постоянной э. д. с), поэтому здесь приведено конечное выражение для функции переходного тока 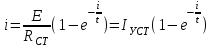 Полученное выражение позволяет построить на графике (см. рис. 8.5) динамическую кривую тока первого приближения 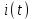 .По этой кривой и нелинейной характеристике (В. А. X. НС) строится динамическая кривая напряжения на нелинейном сопротивлении uHC(t) (см. рис. 8.5). .По этой кривой и нелинейной характеристике (В. А. X. НС) строится динамическая кривая напряжения на нелинейном сопротивлении uHC(t) (см. рис. 8.5).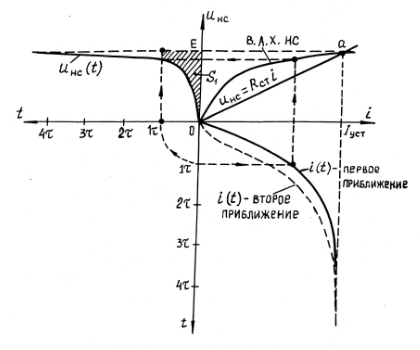 Рис. 8.5. Графические приближения для метода последовательных приближений Для построения uHC(t)достаточно задаться рядом значений текущего времени t, по кривой i(t)первого приближения определить ток и далее, по В. А. X. НС определить значение напряжения на нелинейном сопротивлении. Разделение переменных и интегрирование нелинейного дифференциального уравнения, полученного для исследуемой цепи, дает возможность определить выражение переходного тока второго приближения 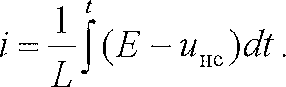 В связи с тем, что в подынтегральную функцию (Е–инс)входит нелинейная зависимость 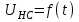 интегрирование осуществляют графически. интегрирование осуществляют графически.Таким образом, для произвольного момента времени t\ соответствующий ток второго приближения определяется следующим выражением: 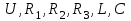 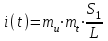 где ти- масштаб напряжения, В/мм ; mt- масштаб времени, с/мм %; S1 - заштрихованная на рис. 8.5 площадь, мм2. Задаваясь различными t, можно построить кривую, более точно выражающую зависимость тока от времени. Полученная кривая тока второго приближения может быть использована при последующем уточнении решения. Для этого необходимо повторить последовательность операций по определению кривой тока второго приближения. Метод кусочно-линейной аппроксимации Данный метод является приближенным к аналитическому и применяется как для расчета переходных процессов, так и для анализа установившегося режима в нелинейных цепях постоянного и переменного токов. Идея метода состоит в том, что характеристика нелинейного элемента заменяется некоторой ломаной линией (аппроксимируется отрезками прямых), достаточно точно отражающей характер заданной нелинейности. Это позволяет перейти от нелинейного дифференциального уравнения к системе линейных и провести расчет используя уже известные методы анализа переходных процессов в линейных цепях (например, классический метод). В основу метода кусочно-линейной аппроксимации положен так на- зываемый метод «припасовывания», суть которого состоит в том, что на- чальное значение тока или напряжения на некотором последующем участке ломаной линии приравнивается конечному значению тока или напряжения на предыдущем участке. Необходимость такого приравнивания вытекает из того положения, что в местах стыка ломаной линии искомая функция не может изменяться скачком (не имеет разрывов). Сущность метода поясним на примере электрической цепи, рассмотренной в предыдущем параграфе. Дифференциальное уравнение, составленное для электрической цепи послекоммутационного режима 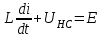 Заменим нелинейную характеристику 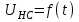 ломаной линией (рис.8.6): для первого участка ломаной линией (рис.8.6): для первого участка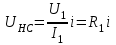 , ,Где 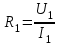 - дифференциальное статическое сопротивления первого участка; для второго участка - дифференциальное статическое сопротивления первого участка; для второго участка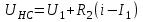 где 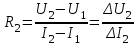 - дифференциальное сопротивление второго участка; для второго участка - дифференциальное сопротивление второго участка; для второго участка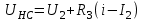  где 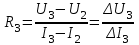 - дифференциальное сопротивление третьего участка - дифференциальное сопротивление третьего участка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||