Практикум по Электротехника и электроника. Задача расчет линейных электрических цепей постоянного тока
 Скачать 4.06 Mb. Скачать 4.06 Mb.
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
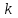 | 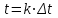 | 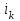  | 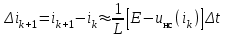  | 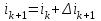 |
| | | | | |
В зависимости от конкретных условий задачи таблица может иметь несколько иной вид (см. пример расчета переходных процессов в нелинейных электрических цепях).
Недостатком данного метода является постепенное наращивание ошибки, которая для больших значений «к» может оказаться весьма ощутимой. Чем меньше интервал
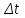 , тем точнее результат.
, тем точнее результат.Метод графического интегрирования
Метод графического интегрирования является наиболее точным из всех вышеперечисленных, поскольку в нем используется действительная характеристика нелинейного элемента без какой-либо ее замены. Однако в противоположность аналитическим методам, он не дает общих связей, позволяющих судить о том, как изменяется процесс при изменении того или иного параметра.
Суть метода состоит в том, что исходя из дифференциального уравнения строится такая кривая, чтобы площадь, ограниченная ею, была пропорциональна времени, соответствующему каждому определенному значению исследуемой функции.
Применяется метод только для решения дифференциального уравнения первого порядка, допускающего разделения переменных.
В качества примера по данному методу рассмотрим переходный процесс, вызванный подключением нелинейной катушки к источнику постоянной э. д. с. (Е)(рис. 8.10, а).
Уравнение, описывающее переходный процесс в рассматриваемой цепи,
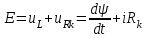
где
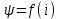 - потокосцепление с обмоткой катушки, нелинейно зависящее от тока
- потокосцепление с обмоткой катушки, нелинейно зависящее от тока 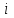 (рис.8.10,б).
(рис.8.10,б).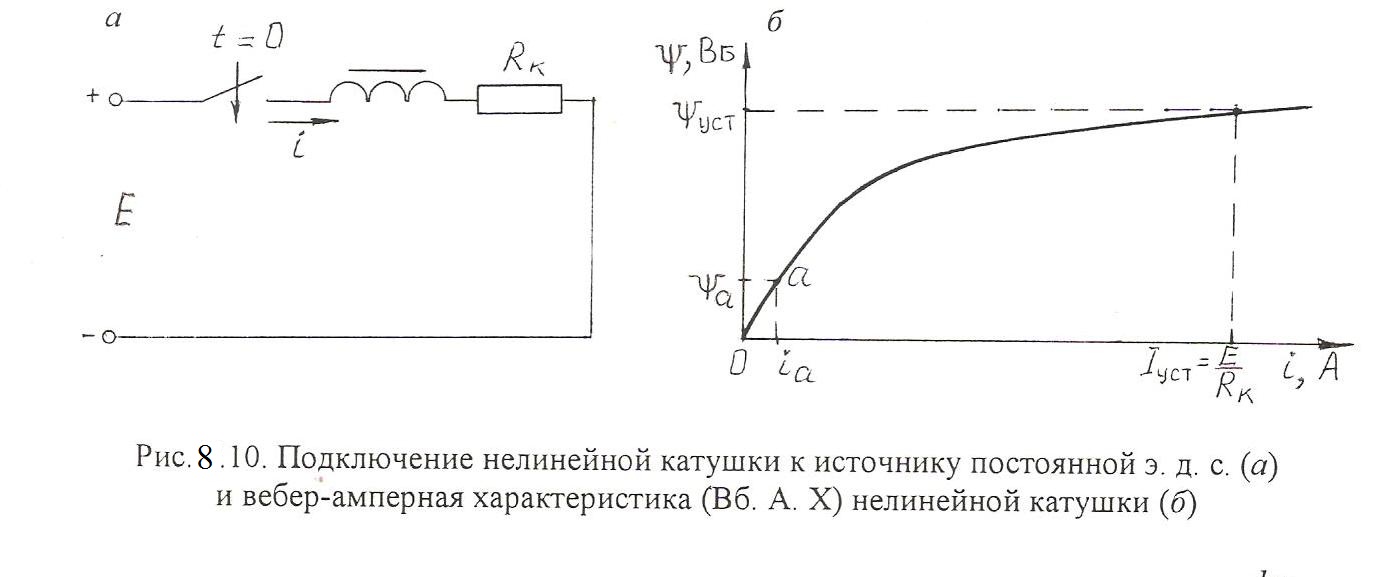
Разделяя переменные в полученном выражении, имеем
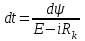 , откуда
, откуда 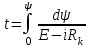 .
.По заданной Вб. А. X. (см. рис. 8.10, б) отроим кривую зависимости подынтегрального выражения от потокосцепления (рис. 8.11). Для этого по графику задаемся рядом значений тока в цепи (
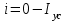 ), определяем потокосцепление
), определяем потокосцепление 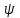 и вычисляем значение подынтегральной функции.
и вычисляем значение подынтегральной функции.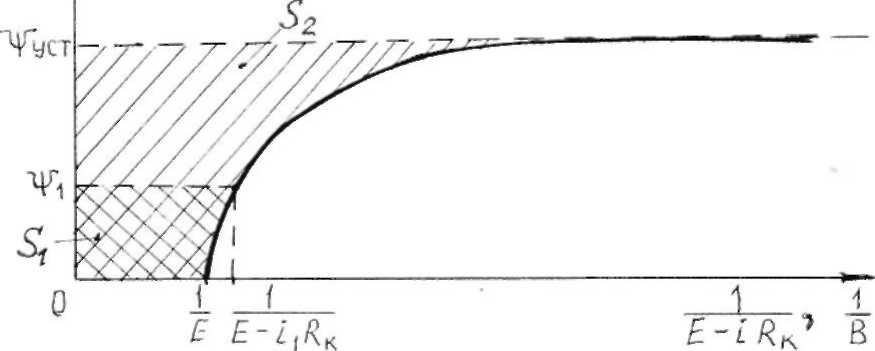
Рис. 8.11. График подынтегральной функции
Время t1, соответствующее значению тока
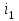 и потокосцеплению
и потокосцеплению 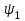 ,определяется по выражению
,определяется по выражению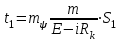 ,
,где
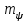 - масштаб, в котором откладывается по оси ординат
- масштаб, в котором откладывается по оси ординат 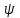 ,Вб/мм;
,Вб/мм;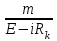 -масштаб подынтегральной функции, 1/В-мм;
-масштаб подынтегральной функции, 1/В-мм; 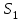 - заштрихованная на рис. 8.11 площадь, мм2 .
- заштрихованная на рис. 8.11 площадь, мм2 .Если задаться несколькими значениями
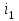 ,
, 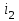 .
. 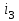 ,... (
,... (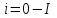 уст) и определить соответствующие значения t1, t2, t3, то можно построить кривую переходного процесса i(t)(динамическую кривую) (рис. 8.12).
уст) и определить соответствующие значения t1, t2, t3, то можно построить кривую переходного процесса i(t)(динамическую кривую) (рис. 8.12).
i,А
Отличительной особенностью кривой переходного тока при подключении нелинейной катушки к источнику постоянной э. д. с. (E) (постоянного напряжения) является то, что в начальной стадии переходного процесса появляется «зона затяжки» или медленное нарастание тока (см. участок «а» рис. 8.12). Объясняется это тем, что дифференциальная индуктивность
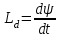 характеризующая длительность переходного процесса
характеризующая длительность переходного процесса 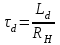 , вначале Вб. А. X. имеет значительно большую величину (см. участок 0-а, рис. 8.10, б).
, вначале Вб. А. X. имеет значительно большую величину (см. участок 0-а, рис. 8.10, б).Пример расчета переходных процессов
в нелинейных электрических цепях
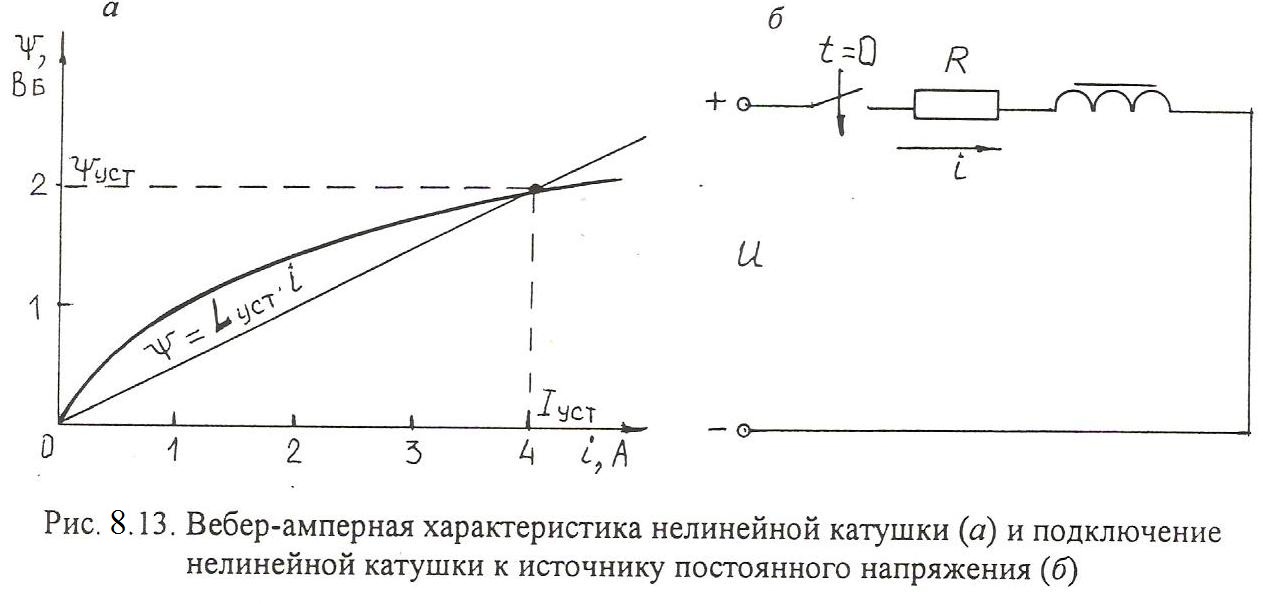
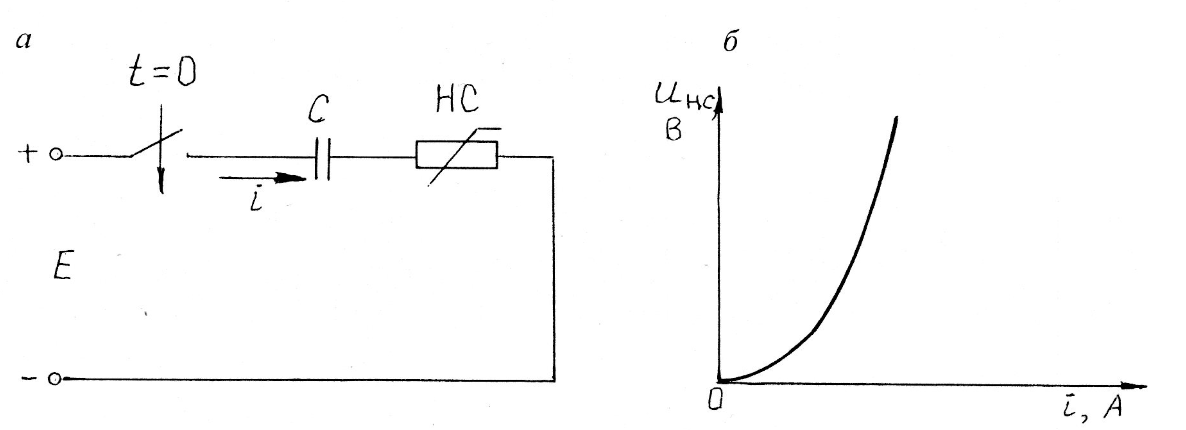
Нелинейная катушка индуктивности, вебер-амперная характеристика (Вб. А. X.) которой представлена на рис. 8.13, а подключается к источнику постоянного напряжения U = 100 В (рис. 8.13, б). Активное сопротивление обмотки R = 25 Ом. Пренебрегая влиянием вихревых токов и не учитывая
явление гистерезиса, определить ток в переходном режиме. Расчет провести различными методами.
Решение методом последовательных приближений
Дифференциальное уравнение для послекоммутационного режима
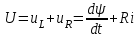 .
.В первом приближении осуществим замену Вб. А. X. прямой линией, проходящей через точку установившегося режима (точка «а», рис. 8.14).
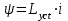

Установившийся режим для данной цепи характерен тем, что
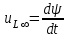 и всё напряжение источника приходится на активное сопротивление катушки. Поэтому ток установившегося режима равен
и всё напряжение источника приходится на активное сопротивление катушки. Поэтому ток установившегося режима равен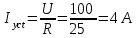 .
.Откладывая этот ток на графике (см. рис. 8.13, а), определяем установившееся значение потокосцепления
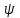 уст = 2 Вб, а также величину индуктивности
уст = 2 Вб, а также величину индуктивности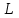 уст=
уст=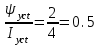 Гн
ГнДалее задача решается чисто аналитически, так как нелинейное дифференциальное уравнение, при подстановке в него
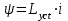 , вырождается в линейное
, вырождается в линейное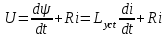 .
.Здесь используется классический метод расчета, когда искомая функция тока находится как сумма двух составляющих
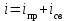
Где
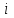 пр =
пр =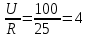 A - принужденная составляющая, определяемая по установившемуся режиму;
A - принужденная составляющая, определяемая по установившемуся режиму; 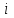 св =
св = 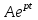 - свободная составляющая, определяемая по виду корней характеристического уравнения.
- свободная составляющая, определяемая по виду корней характеристического уравнения.Корень характеристического уравнения
р=
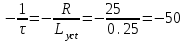 c-1,
c-1,где
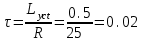 с - постоянная времени электрической цепи.
с - постоянная времени электрической цепи.Общее выражение тока для первого приближения
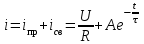 .
.Постоянную интегрирования А находим по независимому условию (по первому закону коммутации) при t= 0, i(0)= 0 (цепь до коммутации была обесточена). Подставляя это условие в последнее уравнение, находим:
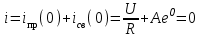
где А =
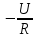 ;
;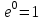 .
.Окончательное выражение для тока первого приближения
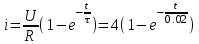 А.
А.По найденному аналитическому выражению на рис. 8.14 построена
динамическая кривая тока первого приближения.
Аналогично проводится расчет и строится динамическая кривая потокосцепления
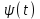 в первом приближении (см. рис. 8.14).
в первом приближении (см. рис. 8.14).Дифференциальное уравнение для потокосцепления в первом
приближении
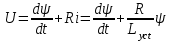
Решая это уравнение классическим методом, находим
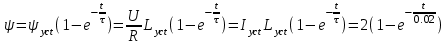 Вб.
Вб.Для построения i(t)второго приближения достаточно задаться рядом значений текущего времени t,по кривой
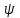 (t) первого приближения определить потокосцепление
(t) первого приближения определить потокосцепление 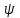 и, далее, по Вб. А. X. нелинейной индуктивностиопределить соответствующее значение тока (см. рис. 8.14).
и, далее, по Вб. А. X. нелинейной индуктивностиопределить соответствующее значение тока (см. рис. 8.14).Графическое интегрирование исходного дифференциального уравнения дает возможность построить динамическую кривую потокосцепления
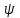 (t) во втором приближении
(t) во втором приближении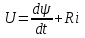
Разделяя переменные и интегрируя левую и правую части уравнения, находим
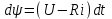 ;
;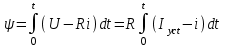 .
.При графическом интегрировании полученного выражения под знак интеграла входит функция i(t),токи которой необходимо брать из кривой тока второго приближения.
На рис. 8.14. для момента времени t1показа площадь S1, ограниченная кривой тока второго приближения. Эта площадь и определяет потокосцепление
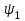 .Задаваясь текущим временем tи вычисляя соответствующие площади, находим значения потокосцепления
.Задаваясь текущим временем tи вычисляя соответствующие площади, находим значения потокосцепления 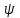 для кривой второго приближения.
для кривой второго приближения.В связи с изменением масштаба площади Sпри печатании данного методического указания на ротапринте, здесь приведена только форма таблицы, по данным которой была построена кривая
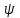 (t)второго приближения (см. рис. 8.14).
(t)второго приближения (см. рис. 8.14).| t, с | 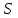 , мм2 , мм2 | 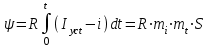 , Вб , Вб |
| | | |
| где mj - масштаб тока, А/мм; mt - масштаб времени, с/мм; S - площадь, ограничен- ная кривой тока второго приближения (заштрихованная на рис. 8.14), мм2. | ||
Процедура построенния динамической кривой тока третьего приближения аналогичная той, которая была рассмотрена выше при построении
кривой второго приближения. Для этого использовалась кривая потокосцепления
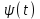 второго приближения и Вб. А. X. нелинейной индуктивности (см. рис. 8.14).
второго приближения и Вб. А. X. нелинейной индуктивности (см. рис. 8.14).Решение методом кусочно-линейной аппроксимации
Нелинейное дифференциальное уравнение для исследуемой цепи
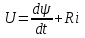
Проведем аппроксимацию Вб. А. X. двумя отрезками прямых линий, проходящих через точку «в» и точку установившегося режима «а» (рис. 8.15).
Уравнения прямых:
для первого участка
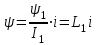
где
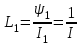 Гн - дифференциальная индуктивность (статическая) первого участка;
Гн - дифференциальная индуктивность (статическая) первого участка;для второго участка
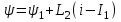 ,
,где
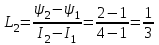 Гн - дифференциальная индуктивность второго участка.
Гн - дифференциальная индуктивность второго участка.Дифференцируя левые и правые части уравнений прямых и подставляя найденные производные в нелинейное дифференциальное уравнение, осуществляем переход к системе линейных уравнений для каждого из участков.
Дифференциальное уравнение первого участка
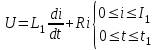

Дифференциальное уравнение второго участка

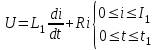
Общее решение полученных уравнений:
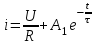 ;(
;(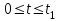 );
);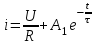 ; (
; (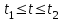 )
)Где
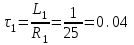 - постоянная времени для первого участка, с;
- постоянная времени для первого участка, с;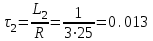 - постоянная времени для второго участка, с; А1и A2- постоянные интегрирования, А.
- постоянная времени для второго участка, с; А1и A2- постоянные интегрирования, А.По первому закону коммутации для данной цепи при t= 0, i(0) = 0
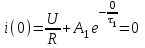 или
или 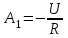 .
.Окончательное выражение переходного тока на первом участке, А
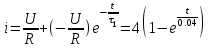
Постоянную интегрирования А2 находим из граничных условий при
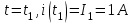 (из графика на рис. 8.15)
(из графика на рис. 8.15)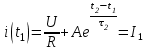 или
или 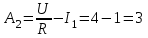 А.
А.Окончательное выражение переходного тока на втором участке:
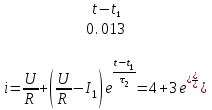 А.
А.Момент времени перехода рабочей точки на второй участок
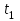 находим также из граничных условий при t = t1, i(t1) = 1 А.
находим также из граничных условий при t = t1, i(t1) = 1 А. 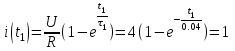 А или
А или 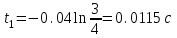
На рис. 8.16 по найденным аналитическим выражениям построена динамическая кривая переходного тока i(t).
Рис. 8.16. Динамическая кривая переходного тока
Решение методом аналитической аппроксимации
Воспользуемся квадратичной зависимостью, достаточно точно отражаемой В. А. X. нелинейной катушки в рабочем диапазоне (см. рис. 8.1, а)
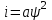 ,
,где а = 1 - коэффициент пропорциональности, А2/Вб.
Подставляя эту зависимость в исходное дифференциальное уравнение, находим
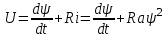
После разделения переменных
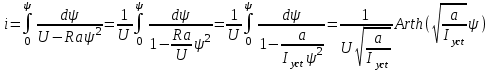 ,
,откуда
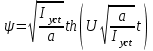
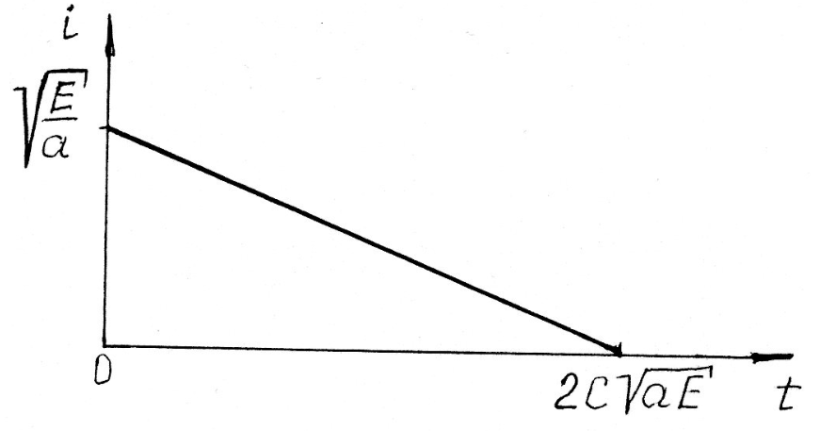
Окончательное выражение функции переходного тока в цепи, А
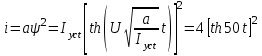
В данном случае при t
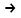
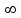 ,
,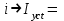 4 А.
4 А.
По найденному аналитическому выражению в масштабе строим график переходного процесса (рис. 8. 17).
Решение методом последовательных интервалов
Дифференциальное уравнение для исследуемой цепи (см.рис.8.13,б)
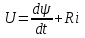
Запишем это уравнение в конечных приращениях
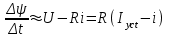 или
или 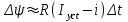
Разбиваем длительность переходного процесса на ряд малых, одинаковых по времени интервалов
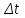 . В пределах каждого интервала полагаем
. В пределах каждого интервала полагаем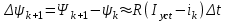 ,
,где
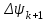 - конечное приращение потокосцепления, Вб;
- конечное приращение потокосцепления, Вб; 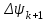 и
и 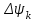 - мгновенные значения потокосцепления в начале и в конце интервала времени, Вб;
- мгновенные значения потокосцепления в начале и в конце интервала времени, Вб; 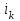 - мгновенное значение тока в начале к-го интервала (определяется поВб. А. X. нелинейной катушки для соответствующего потокосцепления), А.
- мгновенное значение тока в начале к-го интервала (определяется поВб. А. X. нелинейной катушки для соответствующего потокосцепления), А.Ориентировочно длительность интервала времени Atопределяем по постоянной времени
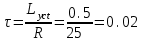 с,
с, 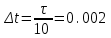 с.
с.В начале первого интервала времени
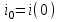 = 0 и
= 0 и 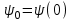 = 0 (в соответствии с первым законом коммутации). Приращение потокосцепления на первом интервале
= 0 (в соответствии с первым законом коммутации). Приращение потокосцепления на первом интервале 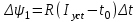 =25-4-0,002=0,2Вб, откуда
=25-4-0,002=0,2Вб, откуда 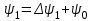 = 0,02 Вб.
= 0,02 Вб.Откладывая найденное значение потокосцепления в конце первого интервала времени
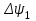 = 0,2 Вб на вебер-амперной характеристике (см.рис. 8.13, а),находим значение тока i\в конце этого интервала. Из графика определяем i1=0,1 А.
= 0,2 Вб на вебер-амперной характеристике (см.рис. 8.13, а),находим значение тока i\в конце этого интервала. Из графика определяем i1=0,1 А.Далее идет процесс вычислений на втором интервале, при этом полагаем, что мгновенные значения потокосцепления и тока в конце первого интервала времени равны их мгновенным значениям в начале второго интервала. Данные расчета сведены в табл. 8.3.
Таблица 8.3
Расчетная таблица метода последовательных интервалов
| к | 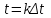 , с , с | 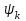 , Вб , Вб | 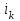 , А , А | 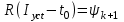 , Вб , Вб | 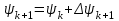 , Вб , Вб |
| 0 | 0 | 0 | 0 | 0,2 | 0,2 |
| 1 | 0.002 | 0.2 | 0.1 | 0.195 | 0.395 |
| 2 | 0.004 | 0.395 | 0.25 | 0.187 | 0,582 |
| 3 | 0.006 | 0,582 | 0.4 | 0.130 | 0,752 |
| 4 | 0,008 | 0,752 | 0,56 | 0,172 | 0,924 |
| 5 | 0,010 | 0,924 | 0.85 | 0.157 | 1,082 |
| 6 | 0.012 | 1.082 | 1.71 | 0.141 | 1.223 |
| 7 | 0.014 | 1.223 | 1.496 | 0.125 | 1,348 |
| 8 | 0.016 | 1.348 | 1,818 | 0.109 | 1.457 |
| 9 | 0,018 | 1,457 | 2,124 | 0.094 | 1.551 |
| 10 | 0.02 | 1,551 | 2,406 | 0.0796 | 1.631 |
| 11 | 0.022 | 1,631 | 2.659 | 0.067 | 1,698 |
| 12 | 0,024 | 1,696 | 2.882 | 0.0558 | 1,754 |
| 13 | 0.026 | 1,754 | 3.075 | 0.0462 | 1.799 |
| 14 | 0.028 | 1,799 | 3,239 | 0,038 | 1.838 |
| 15 | 0,03 | 1,883 | 3,378 | 0.0311 | 1.869 |
| 16 | 0,032 | 1.869 | 3,493 | 0.0253 | 1.894 |
| 17 | 0,034 | 1.894 | 3,588 | 0.0205 | 1.915 |
| 18 | 0,036 | 1.915 | 3,667 | 0.0166 | 1,932 |
| 19 | 0,038 | 1.932 | 3.731 | 0,0134 | 1.945 |
| 20 | 0.04 | 1.945 | 3.783 | 0.0108 | 1.956 |
| 21 | 0.042 | 1,956 | 3.825 | 0,0087 | 1,965 |
| 22 | 0.044 | 1,965 | 3.859 | 0,0070 | 1.972 |
| 23 | 0.046 | 1.972 | 3.887 | 0.0056 | 1,977 |
| 24 | 0.048 | 1,977 | 3,909 | 0,0045 | 1.982 |
| 25 | 0.05 | 1,982 | 3.927 | 0.0036 | 1,985 |
| 26 | 0.052 | 1.985 | 3.941 | 0,0029 | 1.988 |
| 27 | 0.054 | 1.988 | 4 | 0.023 | 2 |
По данным табл. 8.3 строится график переходного процесса (см. рис.8,17)
Решение методом графического интегрирования
Дифференциальное уравнение для исследуемой цепи
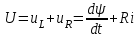 .
.Разделяя переменные, находим:
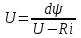 , откуда
, откуда 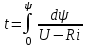
Полученные выражения позволяют осуществить графическое
интегрирование и определить текущее время для соответствующихзначений тока iи потокосцепления
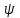 .
.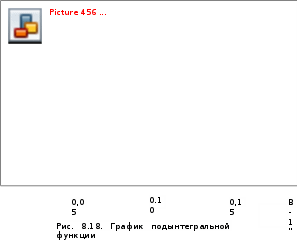
На рис. 8.18 представлен график подынтегральной функции
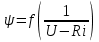 и ограничиваемая им площадь, пропорциональная текущему времени
и ограничиваемая им площадь, пропорциональная текущему времени 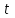 .
.
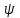 , Вб
, Вб2
Все вычисления по определению точек этого графика, а также соответствующих площадей, приведены в табл. 8.4.
Таблица 7.4
Расчетные данные для построения подынтегральной функции, текущего времени и динамической кривой тока
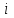 , А , А | 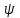 , Вб , Вб | 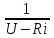 , В-1 , В-1 | S,М2 | 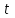 ,с ,с |
| 0 | 0 | 0,01 | 0 | 0 |
| 0,2 | 0,447 | 0,0105 | 273 | 0,0055 |
| 0.4 | 0,632 | 0,0111 | 363 | 0,0073 |
| 0,6 | 0,775 | 0,0117 | 4424 | 0,0085 |
| 0,8 | 0,894 | 0,0125 | 512 | 0.0102 |
| 1,0 | 1.0 | 0,0133 | 560 | 0,0112 |
| 1,2 | 1.095 | 0,0143 | 660 | 0,0132 |
| 1,4 | 1,183 | 0,0154 | 711 | 0,0142 |
| 1,6 | 1,265 | 0,0166 | 786 | 0,0157 |
| 1,8 | 1,342 | 0,0182 | 848 | 0,0170 |
| 2,0 | 1,414 | 0,02 | 933 | 0,0187 |
| 2.2 | 1,483 | 0,0222 | 991 | 0,0198 |
| 2,4 | 1.549 | 0.025 | 1067 | 0,0213 |
| 2,6 | 1,612 | 0,0286 | 1136 | 0.0227 |
| 2,8 | 1,673 | 0,0333 | 1246 | 0.0249 |
| 3,0 | 1.732 | 0,04 | 1358 | 0,0272 |
| 3,2 | 1.788 | 0,05 | 1489 | 0.0298 |
| 3;4 | 1,844 | 0,0666 | 1617 | 0,0323 |
| 3.6 | 1.897 | 0,1 | 1798 | 0.0360 |
| 3.8 | 1,949 | 0.2 | 1993 | 0.0399 |
| 4.0 | 2 | ос | -2368 | -0,0474 |
Следует отметить, что потокосцепление
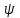 для заданных значений тока в табл. 8.4 определены по Вб. А. X. нелинейной катушки (см. рис. 8.13,а).
для заданных значений тока в табл. 8.4 определены по Вб. А. X. нелинейной катушки (см. рис. 8.13,а).По данным табл. 8.4 построена динамическая кривая переходного тока i(t)(рис. 8.19).

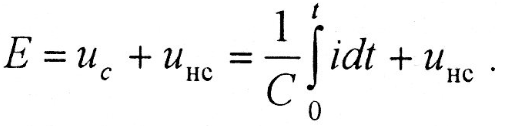
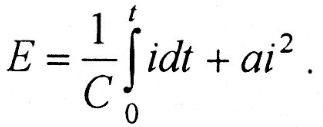
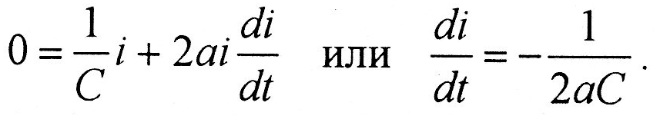
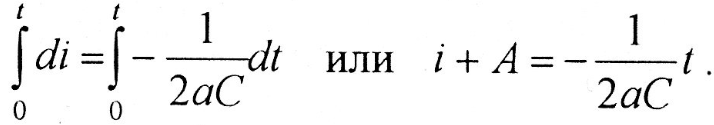
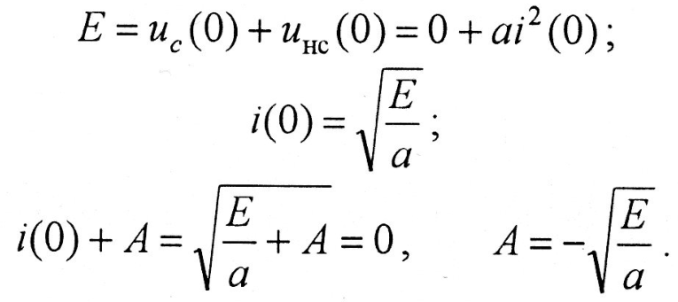
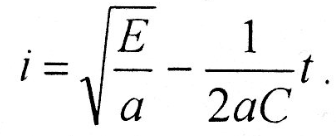
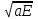
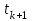 значение искомой функции может быть представлено как
значение искомой функции может быть представлено как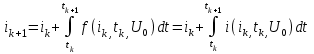
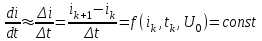
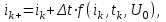
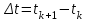 - конечное приращение по времени (интервал по времени);
- конечное приращение по времени (интервал по времени);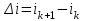 - конечное приращение по току;
- конечное приращение по току; 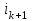 - мгновенные значения
- мгновенные значения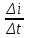
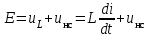
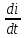 отношением конечных приращении
отношением конечных приращении 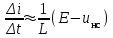 или
или 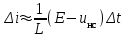
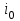 согласно последнему выражению определяется ток в конце первого интервала.
согласно последнему выражению определяется ток в конце первого интервала.