Ответы к госэкзамену по ОЗЗ 2008. Закон О здравоохранении

• Название: Закон О здравоохранении
• Дата: 31.12.2022
• Размер: 2.2 Mb.
• Имя файла: Ответы к госэкзамену по ОЗЗ 2008.doc
• Тип: Закон; #869943
• страница: 29 из 32

б) экстенсивные - показатели удельного веса, структуры, характе­ризуют распределение явления на составные части, его внутреннюю структуру. Вычисляются экстенсивные показатели отношением части явления к целому и выражаются в процентах или долях единицы.



Экстенсивные показатели используются для определения структу­ры явления и сравнительной оценки соотношения составляющих его частей. Экстенсивные показатели всегда взаимосвязаны между собой, т. к. их сумма всегда равна 100 процентам: так, при изучении структуры заболеваемости удельный вес отдельного заболевания мо­жет возрасти:

- при истинном росте числа заболеваний

- при одном и том же его уров­не, если число других заболеваний снизилось

- при снижении числа данного заболевания, если уменьшение числа других заболеваний происходит более быстрыми темпами.

При анализе экстенсивный показатель следует применять с осторожностью и помнить, что им пользуются только для характеристики состава (структуры) явления в данный момент времени и в данном месте.

Примеры использования в работе врача: лейкоцитарная формула; структура населения по полу, возрасту, социальному положению; структура заболеваний по нозологии; структура причин смерти.

в) соотношения - представляют собой соотношение двух самостоя­тельных, независимых друг от друга, качественно разнородных вели­чи, сопоставляемых только логически.



Примеры использования в работе врача: показатели обеспеченности населения врачами, больничными койками; показатели, отражающие число лабораторных исследований на 1 врача и т.д.

г) наглядности - применяются с целью более наглядного и дос­тупного сравнения статистических величин. Показатели наглядности представляют удобный способ преобразования абсолютных, относи­тельных или средних величин в легкую для сравнения форму. При вы­числении этих показателей одна из сравниваемых величин приравни­вается к 100 (или 1), а остальные величины пересчитываются соответственно этому числу.



Показатели наглядности указывают, на сколько процентов или во сколько раз произошло увеличение или уменьшение сравниваемых ве­личин. Показатели наглядности используются чаше всего для сравне­ния данных в динамике, чтобы представить закономерности изучае­мого явления в более наглядной форме.

При пользовании относительными величинами могут быть допущены некоторые ошибки:

1. иногда судят об изменении частоты явления на основе экстенсив­ных показателей, которые характеризуют структуру явления, а не его интенсивность.

2. нельзя складывать и вычитать статистические показатели, кото­рые рассчитаны из совокупностей, имеющих разную численность, ибо это приводит к грубым искажениям показателя.

3. при расчете специальных показателей следует правильно выби­рать знаменатель для расчета показателя: например, показатель послеоперационной летальности необходимо рассчитывать по отно­шению к оперированным, а не всем больным.

4. при анализе показателей следует учитывать фактор времени: нельзя сравнивать между собой показатели, вычисленные за раз­личные периоды времени (показатель заболеваемости за год и за полугодие), что может привести к ошибочным суждениям.

5. нельзя сравнивать между собой общие интенсивные показатели, вычисленные из неоднородных по составу совокупностей, пос­кольку неоднородность состава среды может влиять на величину интенсивного показателя.

111. Показатели соотношения и наглядности. Методика вычисления, использование в здравоохранении – см. вопрос 110.

112. Графические изображения в статистике. Виды диаграмм, правила их построения.

Результаты статистического исследования могут быть представле­ны в виде графических изображений, что позволяет более наглядно продемонстрировать полученные результаты и облегчает проведение анализа.

Существует несколько видов графических изображений, наиболее часто используют диаграммы (линейные, радиальные, столбиковые, ленточные, гистограммы, секторные и др.), картограммы, карто­диаграммы.

При построении графических изображений необходимо соблюдать следующие правила:

- данные на графике должны размещаться слева направо и снизу вверх;

- обязательное условие при построении графика - соблюдение мас­штабности;

- нулевые точки шкал при наличии возможности должны быть изобра­жены на диаграмме

- цифры, показывающие деление шкал, помещаются слева или внизу соответствующей шкалы;

- линии, представляющие диаграмму изображаемого явления, сле­дует делать иного вида, нежели вспомогательные линии;

- на кривой, отражающей динамику явления, необходимо отметить все точки, соответствующие отдельным наблюдениям;

- в диаграммах, показывающих структуру, должна быть оттенена как линия нулевая, так и 100-процентная;

- изображенные графические величины должны иметь цифровые обоз­начения на самом графике или в прилагаемой к нему таблице;

- символы, используемые при построении диаграммы (цвет, штри­ховка, фигуры, знаки), должны быть пояснены;

- каждый график должен иметь четкое, краткое название, отражаю­щее его содержание;

- название диаграммы должно размешаться под рисунком.

Виды диаграмм:

а) линейные диаграммы - позволяют изображать динамику явления (изменение показателей во времени). Линейная диаграмма строится в системе прямоугольных координат, при ее построении следует учи­тывать соотношение между основанием и высотой - абсциссой х и ор­динатой у, основанное на принципе "золотого сечения": это соотно­шение должно быть 1,6:1. На горизонтальной оси (оси абсцисс) откладываются отрезки, обозначающие периоды времени. На верти­кальной оси (оси ординат) откладываются размеры изучаемого явле­ния. Обязательное условие при построении графика - масштабность. На одной диаграмме можно изобразить несколько линий, отличающих­ся друг от друга цветом, толщиной или формой пунктира.

б) радиальные диаграммы (диаграммы полярных координат, линей­но-круговые диаграммы, векторные диаграммы) - применяются для изображения сезонных (подекадных, помесячных, поквартальных) и других колебаний, имеющих замкнутый, циклический характер (за сутки, неделю и т.д.). Для их построения круг делится на столько секторов, на сколько частей разделен период времени, взятый для изучения явления (например, на 12 - при изучении помесячных коле­баний в течение года; на 7 - при изучении явления за неделю). На каждом из радиусов с соблюдением масштабности отмечаются показа­тели, полученные точки соединяют прямыми линиями. Начало марки­ровки радиусов начинается с радиуса, соответствующего нулю граду­сов, и продолжается по часовой стрелке.

в) столбиковые диаграммы - строятся по такому же принципу, как и линейные, в системе координат, с соблюдением масштабности, но в которых вертикально или горизонтально проводимым линиям соответ­ствуют прямоугольники. Эти диаграммы используются для изображе­ния сравнительной величины явления в какой-либо определенный про­межуток времени, например, сравнительной численности населения по странам мира; обеспеченности населения врачами в разные годы и т.д.

г) гистограммы - в виде прямоугольников, треугольников, фигур позволяют изобразить однородные статистические показатели, не связанные друг с другом. Эти диаграммы используются для графичес­кого изображения статистических величин, характеризующих статику явления в разных совокупностях. Они также строятся в системе пря­моугольных координат с соблюдением масштабности. Например, гис­тограммы применяются для графического изображения уровней смер­тности в разных возрастных группах населения; для демонстрации показателей больничной летальности в различных стационарах города; для изображения распространенности туберкулеза в различных со­циально-бытовых группах населения и т.д.

д) секторные диаграммы - используются для демонстрации структуры изучаемого явления, изображения части явления в целом. Они пред­ставляют собой круг, принимаемый за целое (100%), в котором от­дельные секторы соответствуют частям изображаемого явления. Этот вид диаграмм применяется для графического изображения экстенсив­ных показателей. В секторных диаграммах секторы, изображающие от­дельные части изучаемого явления, располагаются в порядке возрас­тания или убывания по движению часовой стрелки и имеют разный цвет или штриховку.

е) внутристолбиковые диаграммы также могут применяться для изоб­ражения структуры явления. При этом высота столбика принимается за 100%, весь столбик делится на составные части, которые соот­ветствуют долям явления в процентах

ж) картограммы - это графические изображения, нанесенные на схе­мы географической карты, на которой различным цветом или штрихов­кой изображены степени распространенности явления по территории

з) картодиаграммы - такие графические изображения, при построе­нии которых на карту или схему карты изучаемой территории прос­тавляются диаграммы (столбиковые, фигурные, линейные)

113. Вариационный ряд, его элементы, виды, правила построения – см. вопрос 114.

114. Средние величины, виды, методика вычисления. Использование в медицине.

Средние величины дают обобщающую характеристику статистичес­кой совокупности по определенному изменяющемуся количественному признаку. Средняя величина характеризует весь ряд наблюдений одним чис­лом, выражающим общую меру изучаемого признака. Она нивелирует случайные отклонения отдельных наблюдений и дает типичную харак­теристику количественного признака.

Требования к средним величинам:

1) качественная однородность совокупности, для которой рассчиты­вается средняя величина - только тогда

она будет объективно отображать ха­рактерные особенности изучаемого явления.

2) средняя величина должна основываться на массовом обобще­нии изучаемого признака, т.к. только тогда она выражает типич­ные размеры признака

Средние величины получаются из рядов распределения (вариа­ционных рядов).

Вариационный ряд- ряд однородных статистических величин, ха­рактеризующих один и тот же количественный учетный признак, отли­чающихся друг от друга по своей величине и расположенных в опре­деленном порядке (убывания или возрастания).

Элементы вариационного ряда:

а) варианта - v - числовое значение изучаемого меняющегося коли­чественного признака.

б) частота - p (pars) или f (frequency) - повторяемость вариант в вариационном ряду, показывающая, как часто встречается та или иная варианта в составе данного ряда.

в) общее число наблюдений- n (numerus) - сумма всех частот: n=ΣΡ. Если общее число наблюдений более 30,статистическая выборка считается большой, если n меньше или равно 30 - малой.

Вариационные ряды бывают:

1. в зависимости от значения варианты:

а) прерывные (дискретные), состоящие из целых чисел

б) непрерывные, когда значения вариант выражены дроб­ным числом. В прерывных рядах смежные варианты отличаются друг от друга на целое число (число ударов пульса, число дыха­ний в минуту, число дней лечения). В непрерывных рядах ва­рианты могут отличаться на любые дробные значения единицы.

2. в зависимости от частоты встречаемости признака:

а) простой - ряд - каждая варианта встречается один раз, т.е. частоты равны единице.

б) обычный - ряд, в котором варианты встречаются более одного ра­за.

в) сгруппированный- ряд, в котором варианты объединены в группы по их величине в пределах определенного ин­тервала с указанием частоты повторяемости всех вариант, входящих в группу.

Сгруппированный вариационный ряд используют при большом числе наблюдений и больном размахе крайних значений вариант.

Обработка вариационного ряда заключается в получении парамет­ров вариационного ряда (средней величины, среднего квадратичес­кого отклонения и средней ошибки средней величины).

3. в зависимости от числа наблюдений:

а) четные и нечетные

б) большой (при числе наблюдений больше 30) и малый (если число наблюдений меньше или равно 30)

Виды средних величин:

а) мода (Мо) - величина признака, чаще других встречающаяся в со­вокупности. За моду принимают варианту, которой соответствует наибольшее количество частот вариационного ряда.

б) Медиана (Me) - величина признака, занимающая срединное значе­ние в вариационном ряду. Она делит вариационный ряд на две рав­ные части.

На величину моды и медианы не оказывают влияния числовые зна­чения крайних вариант, имеющихся в вариационном ряду. Они не всегда могут точно характеризовать вариационный ряд и применяют­ся в медицинской статистике относительно редко. Более точно ха­рактеризует вариационный ряд средняя арифметическая величина.

в) Средняя арифметическая(М, или ) - рассчитывается на осно­ве всех числовых значений изучаемого признака.

Реже применяются другие средние величины: средняя геометрическая (при обработке результатов титрования антител, токсинов, вакцин); средняя квадратическая (при определении среднего диаметра среза клеток, результатов накожных иммунологических проб); средняя кубическая (для определения среднего объема опухолей) и другие.

В простом вариационном ряду, где варианты встречаются только по одному разу, вычисляется средняя арифметическая простая по формуле: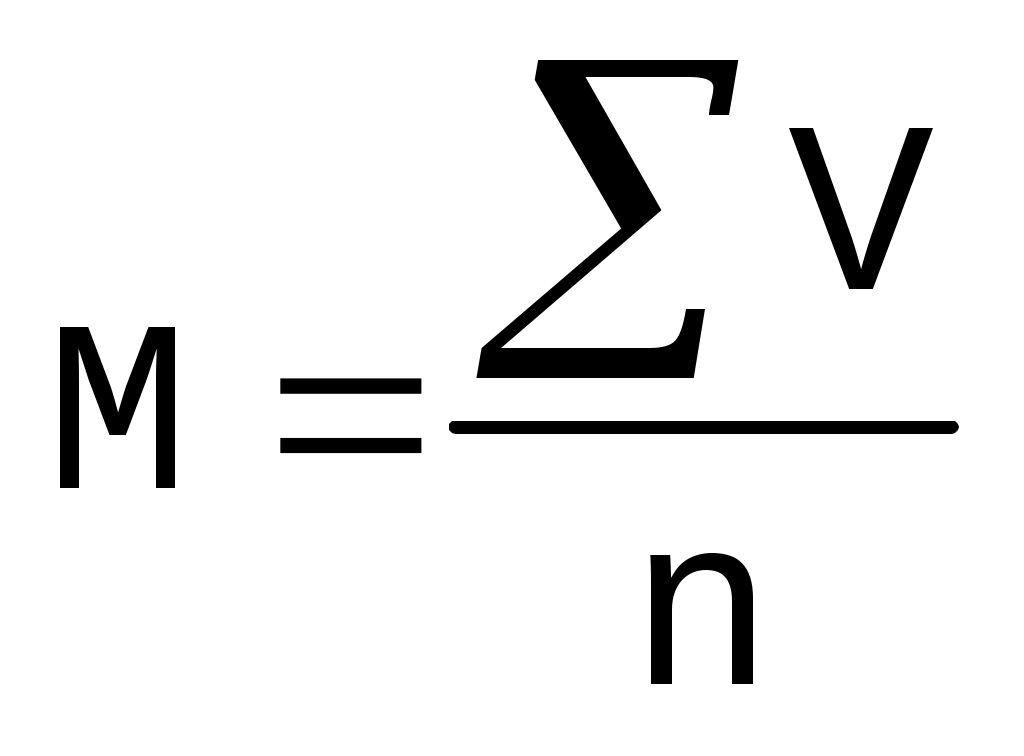

, где V - числовые значения вариант, n - число наблюдений, Σ - знак суммы

В обычном вариационном ряду вычисляется средняя арифметичес­кая взвешенная по формуле:

, где V - числовые значения вариант, р - частота встречаемости вариант, n - число наблюдений.

Средние величины являются важными обобщающими характеристика­ми совокупности. Однако за ними скрываются индивидуальные значе­ния признака. Средние величины не показывают изменчивости, колеб­лемости признака. Если вариационный ряд более компактен, менее рассеян и все от­дельные значения расположены вокруг средней, то средняя величина дает более точную характеристику данной совокупности. Если вариа­ционный ряд растянут, отдельные значения значительно отклоняются от средней, т.е. имеется большая вариабельность количественного признака, то средняя менее типична, хуже отражает в целом весь ряд.

Одинаковые по величине средние могут быть получены из рядов с различной степенью рассеяния, поэтому для характеристики вариационного ряда, помимо средней величины, необходима другая характеристика, позволяющая оценить степень его колеблемости.

Простыми показателями, характеризующими разнообразие признака в изучаемой совокупности, являются

а) лимит - минимальное и максимальное значение количественного признака

б) амплитуда - разность между наибольшим и наименьшим значением вариант.

Применение средних величин:

а) для характеристики физического развития (рост, вес, окружность груди, динамометрия)

б) для оценки состояния здоровья человека путем анализа физиологических, биохимических параметров организма (уровня АД, ЧСС, температуры тела)

в) для анализа деятельности медицинских организаций (среднее число дней работы койки в году и т.д.)

г) для оценки работы врачей (среднее число посещений на одного врача, среднее число хирургических операций, среднечасовая нагрузка врача на приеме в поликлинике)

115. Характеристика разнообразия изучаемого признака. Среднее квадратическое отклонение, методика вычисления.

Приближенный метод оценки колеблемости вариационного ряда - определение лимита и амплитуды, однако не учитывают значений вариант внутри ряда. Основной общепринятой мерой колеблемости количественного приз­нака в пределах вариационного ряда является среднее квадратичес­кое отклонение (σ - сигма). Чем больше среднее квадратическое отклонение, тем степень ко­леблемости данного ряда выше.

Методика расчета среднего квадратического отклонения включает следующие этапы:

1. Находят среднюю арифметическую величину (Μ).

2. Определяют отклонения отдельных вариант от средней арифмети­ческой (d=V-M). В медицинской статистике отклонения от средней обозначаются как d (deviate). Сумма всех от­клонений равняется нулю.

3. Возводят каждое отклонение в квадрат d².

4. Перемножают квадраты отклонений на соответствующие частоты d²*p.

5. Находят сумму произведений ( d²*p)

6. Вычисляют среднее квадратическое отклонение по формуле:

при n больше 30,или при n меньше либо равно 30, где n - число всех вариант.

Значение среднего квадратичного отклонения:

1. Среднее квадратическое отклонение характеризует разброс вариант относительно средней величины (т.е. колеблемость вариационного ряда). Чем больше сигма, тем степень разнообразия данного ряда выше.

2. Среднее квадратичное отклонение используется для сравнительной оценки степени соответствия средней арифметической величины тому вариационному ряду, для которого она вычислена.

Вариации массовых явлений подчиняются закону нормального распределения. Кривая, отображающая это распределение, имеет вид плавной колоколообразной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значениями средней арифметической и среднего квадратического отклонения существует строгая математическая зависимость. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм.

Если в системе прямоугольных координат на оси абсцисс отложить значения количественного признака (варианты), а на оси ординат - частоты встречаемости вариант в вариационном ряду, то по сторонам от средней арифметической равномерно располагаются варианты с большими и меньшими значениями.

Установлено, что при нормальном распределении признака:

- 68,3% значений вариант находится в пределах М1

- 95,5% значений вариант находится в пределах М2

- 99,7% значений вариант находится в пределах М3

3. Среднее квадратическое отлонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М1 обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1 указывает на отклонение изучаемого параметра от нормы.

4. В медицине правило трех сигм применяется в педиатрии для индивидуальной оценки уровня физического развития детей (метод сигмальных отклонений), для разработки стандартов детской одежды

5. Среднее квадратическое отклонение необходимо для характеристики степени разнообразия изучаемого признака и вычисления ошибки средней арифметической величины.

Величина среднего квадра­тического отклонения обычно используется для сравнения колеблемости однотипных рядов. Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и больничная летальность и т.д.), то непосредственное сопоставление размеров сигм невозможно, т.к. среднеквадратичес­кое отклонение - именованная величина, выраженная в абсолютных числах. В этих случаях применяют коэффициент вариации (Cv), представляющий собой относительную величину: процентное отноше­ние среднего квадратического отклонения к средней арифметической.

Коэффициент вариации вычисляется по формуле:



Чем выше коэффициент вариации, тем большая изменчивость данно­го ряда. Считают, что коэффициент вариации свыше 30 % свиде­тельствует о качественной неоднородности совокупности.

116. Ошибка репрезентативности, методика вычисления ошибки средней и относительной величины.

В статистике выделяют два основных метода исследования - сплошной и выборочный. При проведении выборочного исследования обязательным является соблюдение следующих требований: репрезентативность выборочной совокупности и достаточное число единиц наблюдений. При выборе единиц наблюдения возможны ошибки смещения, т.е. такие события, появление которых не может быть точно предсказуемым. Эти ошибки являются объектив­ными и закономерными. При определении степени точности выборочно­го исследования оценивается величина ошибки, которая может прои­зойти в процессе выборки - случайная ошибка репрезентативности (m) - является фактической разностью между средними или относительными величинами, полученными при проведении выборочного исследования и аналогичными величинами, которые были бы получены при проведении исследования на гене­ральной совокупности.

Оценка достоверности результатов исследования предусматривает определение:

1. ошибки репрезентативности

2. доверительных границ средних (или относительных) величин в генеральной совокупности

3. достоверности разности средних (или относительных) величин (по критерию t)