Ответы к госэкзамену по ОЗЗ 2008. Закон О здравоохранении
 Скачать 2.2 Mb.
|
|
Расчет ошибки репрезентативности (mм) средней арифметической величины (М):   , где σ - среднее квадратическое отклонение; n - численность выборки (>30).Расчет ошибки репрезентативности (mР) относительной величины (Р):  , где Р - соответствующая относительная величина (рассчитанная, например, в %);q =100 - Ρ% - величина, обратная Р; n - численность выборки (n>30) В клинических и экспериментальных работах довольно часто приходится использовать малую выборку, когда число наблюдений меньше или равно 30. При малой выборке для расчета ошибок репрезентативности, как средних, так и относительных величин, число наблюдений уменьшается на единицу, т.е.  ;  .Величина ошибки репрезентативности зависит от объема выборки: чем больше число наблюдений, тем меньше ошибка. Для оценки достоверности выборочного показателя принят следующий подход: показатель (или средняя величина) должен в 3 раза превышать свою ошибку, в этом случае он считается достоверным. Знание величины ошибки недостаточно для того, чтобы быть уверенным в результатах выборочного исследования, так как конкретная ошибка выборочного исследования может быть значительно больше (или меньше) величины средней ошибки репрезентативности. Для определения точности, с которой исследователь желает получить результат, в статистике используется такое понятие, как вероятность безошибочного прогноза, которая является характеристикой надежности результатов выборочных медико-биологических статистических исследований. Обычно, при проведении медико-биологических статистических исследований используют вероятность безошибочного прогноза 95% или 99%. В наиболее ответственных случаях, когда необходимо сделать особенно важные выводы в теоретическом или практическом отношении, используют вероятность безошибочного прогноза 99,7% Определенной степени вероятности безошибочного прогноза соответствует определенная величина предельной ошибки случайной выборки (Δ - дельта), которая определяется по формуле: Δ=t * m , где t - доверительный коэффициент, который при большой выборке при вероятности безошибочного прогноза 95% равен 2,6; при вероятности безошибочного прогноза 99% - 3,0; при вероятности безошибочного прогноза 99,7% - 3,3, а при малой выборке определяется по специальной таблице значений t Стьюдента. Используя предельную ошибку выборки (Δ), можно определить доверительные границы, в которых с определенной вероятностью безошибочного прогноза заключено действительное значение статистической величины, характеризующей всю генеральную совокупность (средней или относительной). Для определения доверительных границ используются следующие формулы: 1) для средних величин:  ,где Мген - доверительные границы средней величины в генеральной совокупности;Мвыб- средняя величина, полученная при проведении исследования на выборочной совокупности; t - доверительный коэффициент, значение которого определяется степенью вероятности безошибочного прогноза, с которой исследователь желает получить результат; mM - ошибка репрезентативности средней величины. 2) для относительных величин:  , где Рген - доверительные границы относительной величины в генеральной совокупности; Рвыб- относительная величина, полученная при проведении исследования на выборочной совокупности; t - доверительный коэффициент; mP - ошибка репрезентативности относительной величины.Доверительные границы показывают, в каких пределах может колебаться размер выборочного показателя в зависимости от причин случайного характера. При малом числе наблюдений (n<30), для вычисления доверительных границ значение коэффициента t находят по специальной таблице Стьюдента. Значения t расположены в таблице на пересечении с избранной вероятностью безошибочного прогноза и строки, указывающей на имеющееся число степеней свободы (n), которое равно n-1. 117. Оценка достоверности различий относительных и средних величин. Критерии «t». При проведении медико-биологических исследований на двух сравниваемых совокупностях возникает необходимость определить не только их различие, но и его достоверность. Метод оценки достоверности разности показателей или средних величин позволяет установить, существенны ли выявленные различия, или они являются результатом действия случайных причин. В основе метода лежит определение критерия достоверности "t", который рассчитывается по специальным формулам для средних и относительных величин: для средних: 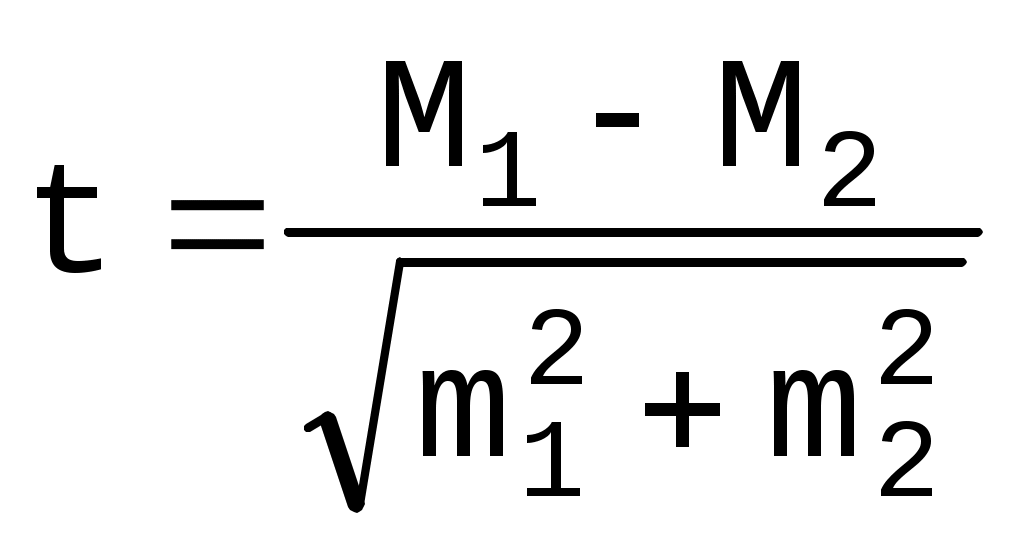 , а для относительных величин  , где Μ1, Μ2, P1 и P2 - статистические величины, полученные при проведении выборочных исследований: m1 и m2 - их ошибки репрезентативности; t - коэффициент достоверности. При большой выборке различие достоверно при t>2, что соответствует вероятности безошибочного прогноза равной или более 95%. При величине коэффициента достоверности t<2 степень вероятности безошибочного прогноза менее 95%. При такой степени вероятности мы не можем утверждать, что полученная разность показателей достоверна с достаточной степенью вероятности. В этом случае необходимо получить дополнительные данные, увеличив число наблюдений. Если после увеличения численности выборки, и, соответственно, уменьшения ошибки репрезентативности, различие продолжает оставаться недостоверным, можно считать доказанным, что между сравниваемыми совокупностями не обнаружено различий по изучаемому признаку. Для определения достоверности различий между двумя показателями или средними величинами при малом числе наблюдений критерий достоверности оценивается по таблице значений критерия t Стьюдента по числу степеней свободы, которое при этом определяется как сумма чисел наблюдений в каждой группе без двух. 118. Динамический ряд, виды, методы выравнивания. Показатели динамического ряда, методика вычисления. При изучении динамики какого-либо явления прибегают к построению динамического ряда. Динамический ряд - это ряд однородных статистических величин, показывающих изменение какого-либо явления во времени и расположенных в хронологическом порядке через определенные промежутки времени. Числа, составляющие динамический ряд, называются уровнями. Уровень ряда- размер (величина) того или иного явления, достигнутый в определенный период или к определенному моменту времени. Уровни ряда могут быть представлены абсолютными, относительными или средними величинами. Динамические ряды делятся на а) простые (состоящие из абсолютных величин) - могут быть: 1) моментными- состоит из величин, характеризующих явление на какой-то определенный момент (статистические сведения, обычно регистрируемые на начало или конец месяца, квартала, года) 2) интервальными - состоит из чисел, характеризующих явление за определенный промежуток времени (интервал) - за неделю, месяц, квартал, год (данные о числе родившихся, умерших за год, число инфекционных заболеваний за месяц). Особенностью интервального ряда является то, что его члены можно суммировать (при этом укрупняется интервал), или дробить. б) сложные (состоящие из относительных или средних величин). Динамические ряды могут подвергаться преобразованиям, целью которых является выявление особенностей изменения изучаемого процесса, а также достижение наглядности. Показатели динамического ряда: а) уровни ряда - величины членов ряда. Величина первого члена ряда носит название начального (исходного) уровня, величина последнего члена ряда - конечного уровня, средняя величина из всех членов ряда называется средним уровнем. б) абсолютный прирост (убыль) - величина разности между последующим и предыдущим уровнями; прирост выражается числами с положительным знаком, убыль - с отрицательным знаком. Значение прироста или убыли отражают изменения уровней динамического ряда за определенный промежуток времени. в) темп роста (снижения) - показывает отношение каждого последующего уровня к предыдущему уровню и обычно выражается в процентах. г) темп прироста (убыли) - отношение абсолютного прироста или убыли каждого последующего члена ряда к уровню предыдущего, выраженное в процентах. Темп прироста может быть вычислен также по формуле: Темп роста - 100% Абсолютное значение одного процента прироста (убыли) - получается от деления абсолютной величины прироста или убыли на показатель темпа прироста или убыли за тот же период. Для более наглядного выражения нарастания или убывания ряда можно преобразовать его путем вычисления показателей наглядности, показывающих отношение каждого члена ряда к одному из них, принятому за сто процентов. Иногда динамика изучаемого явления представлена не в виде непрерывно меняющегося уровня, а отдельными скачкообразными изменениями. В этом случае для выявления основной тенденции в развитии изучаемого явления прибегают к выравниванию динамического ряда. При этом могут быть использованы следующие приемы: а) укрупнение интервала - суммирование данных за ряд смежных периодов. В результате получаются итоги за более продолжительные промежутки времени. Этим сглаживаются случайные колебания и более четко определяется характер динамики явления. б) вычисление групповой средней - определение средней величины каждого укрупненного периода. Для этого необходимо суммировать смежные уровни соседних периодов, а затем сумму разделить на число слагаемых. Этим достигается большая ясность изменений во времени в) вычисление скользящей средней - в некоторой степени устраняет влияние случайных колебаний на уровни динамического ряда и более заметно отражает тенденцию явления. При ее вычислении каждый уровень ряда заменяется на среднюю величину из данного уровня и двух соседних с ним. Чаще всего суммируются последовательно три члена ряда, но можно брать и больше г) графический метод - выравнивание от руки или с помощью линейки, циркуля графического изображения динамики изучаемого явления. д) выравнивание методом наименьших квадратов - один из наиболее точных способов выравнивания динамического ряда. Метод преследует цель устранить влияние временно действующих причин, случайных факторов и выявить основную тенденцию в динамике явления, вызванную воздействием только длительно действующих факторов. Выравнивание производится по линии, наиболее соответствующей характеру динамики изучаемого явления, при наличии основной тенденции к росту или снижению частоты явления. Такой линией является обычно прямая, которая наиболее точно характеризует основное направление изменений, однако существуют и другие зависимости (квадратическая, кубическая и т.д.). Этот метод позволяет дать количественную оценку выявленной тенденции, оценить средние темпы ее развития и рассчитать прогнозируемые уровни на следующий год. 119. Особенности проведения клинического исследования. Клинико-статистическое исследование - использование статистических методов при обработке результатов клинических, экспериментальных и лабораторных исследований; позволяет с количественной точки зрения оценить достоверность результатов исследования и решить ряд других задач. Особенности клинико-статистического исследования: а) выборочное исследование б) выборка малая в) результаты обрабатываются не параметрическими методами исследования г) наличие всегда конкретной группы либо копии (паракопии) д) единица наблюдения чаще всего - пациент 120. Основные ошибки при проведении статистического исследования. Точность статистического наблюдения - степень соответствия величины какого-либо показателя (значения признака), определенной путем статистического измерения, действительной его величине. Ошибка статистического наблюдения - расхождение между измеренным и действительным значениями изучаемой величины. Методы проверки данных статистического наблюдения: а) счетный контроль - проверка итогов и проверочный расчет показателей (четко устанавливается наличие ошибки); б) логический контроль - сопоставление полученных данных с другими известными признаками, показателями (выявляются неправдоподобные случаи). Виды ошибок статистического наблюдения по источнику происхождения: 1. Непреднамеренные а) для сплошного и несплошного статистического исследования а1. случайные - связаны с невнимательностью, небрежностью регистратора, неточностью измерительных приборов а2. систематические - ошибки округления возраста и сумм, забываемости "второстепенных расходов" (они однонаправленны) б) для несплошного статистического исследования а3. репрезентативности а3.1 - случайные - ошибки из-за недостаточной полноты охвата а3.2 - систематические - из-за отклонения структур выборочной и генеральной совокупностей 2. Преднамеренные (злостные) а) первого рода - из-за применения несовершенных способов статистического наблюдения при наличии более совершенных б) второго рода - из-за применения несовершенных организационных схем проведения статистического наблюдения 121. Рынок: сущность, функции, структура и инфраструктура. Первоначально в древности рынок был местом обмена товаров, в настоящее время рынок – совокупность экономических отношений между производителями и потребителями, основанная на децентрализованном безличностном механизме ценовых сигналов; это сфера свободного обращения товаров, капиталов, движения рабочей силы. Сущность рынка – обмен результатами труда, посредник – деньги. Условия возникновения рынка: - общественное разделение труда и специализация производства - экономическая обособленность субъектов рыночного производства - свободный обмен ресурсами Условия функционирования рынка: - свобода экономической деятельности - многообразие форм собственности - ликвидация монополизма в производстве и реализации товара - создание правовой базы - открытость экономики - устойчивость финансовой и денежной системы - социальная защищенность населения Функции рынка: а) регулирующая: рынок – наиболее совершенный инструмент саморегуляции товарного производства б) стимулирующая: рынок стимулирует эффективность производства, побуждая создавать товар с наименьшими затратами в) рынок обеспечивает окончательное признание общественной значимости произведенного продукта и затраченного на него труда г) информационная – рынок – богатый источник информации (цены) д) в условиях углубления внутри- и межгосударственного разделения труда и расширения кооперационных связей рыночные отношения обеспечивают пропорциональность в товарообороте между различными хозяйствами е) санирующая – рынок «очищает» производство от избыточных предприятий ж) функция дифференциации производителей Структура рынка по объекту рыночных отношений: - товарный: 1) потребительский; 2) рынок информации; 3) рынок средств производства; 4) рынок интеллектуального продукта - финансовый: 1) рынок капиталов; 2) рынок ценных бумаг; 3) рынок труда; 4) рынок кредитов; 5) валютно-денежный рынок - рынок факторов производства Виды рынков: 1. Средства производства 2. Предметы народного потребления 3. Рабочей силы 4. Ценных бумаг (акции, облигации займа, сертификаты, векселя и др.) 5. Научных идей и технических решений 6. Золота 7. Валюты и др. Любой рынок работает на основе законов стоимости, денежного обращения, прибыли, спроса и предложения, конкуренции, монополии, предельной полезности и др. Инфраструктура – совокупность взаимосвязанных организаций, учреждений и служб, обеспечивающих свободное движение товаров, капиталов и рабочей силы: банки, торговые дома, аукционы, выставки, биржи, страховые компании, ярмарки и т.д. 122. Механизм рыночного ценообразования. Равновесие рынка. Состояние рыночной экономики оценивается спросом, предложением и их взаимоотношениями. Спрос - потребность, обеспечиваемая денежными средствами; то количество товаров и услуг, которое потребитель может купить по цене, сложившейся на рынке. Свойство спроса: при прочих равных условиях снижение цены приводит к увеличению спроса и наоборот. Обратная связь – это закон спроса, он определяется 3 причинами: 1) снижение цен увеличивает число покупателей; 2) покупатель получает меньше удовольствия от каждой последующей единицы продукта; 3) действие закона споса можно объяснить эффектом дохода и эффектом замещения. |