СУЛА. Закон регулирования на работу системы стабилизации (движение крена). В реальных системах переключение рулей отстает на время
 Скачать 1.09 Mb.
|
1Для преобразования по Лапласу функции у(х,t)введено обозначение 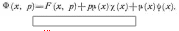 (9) где Члены в последнемвыражении учитывают начальные условия (6) в соответствии с известной формулой 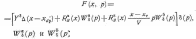  Изображение поперечной погонной нагрузки в нашем примере имеет видгде - передаточные функции абсолютно жесткого летательного аппарата. Граничные условия (7) для преобразованного уравнения можно записать так:  (10)Рассмотрим вначале решение однородного уравнения  (11)n Определяющего свободные колебания балки, которые возникнут, если в начальный момент t=0 балка деформирована. Решение этого уравнения удовлетворяет граничным условия (10),когда параметр р2 принимает вполне определенные числовые значения p 2. Они называются собственными значениями, а соответствующие им решения 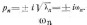 - собственными функциями. В нашей задаче имеет смысл рассматривать только отрицательные собственные значения  , которым соответствует колебательный процесс. В этом случаеn Величина представляет n-ю собственную частоту колебаний балки, которая как тело с распределенными параметрами имеет бесчисленное множество собственных частот, определяемых собственными значениями p 2. Собственная функция  определяет n-ю гармонику деформированной оси балки где An— произвольный пока множитель, не зависящий от х. (Как будет видно ниже, этот множитель зависит от параметра р.) Так как уравнение (11) является линейным, то сумма этих гармоник определяет форму балки:  (12)Это выражение является общим решением уравнения (11), удовлетворяющим граничным условиям (10), но пока не удовлетворяющим начальным условиям (6). Для того чтобы найти решение неоднородного уравнения (9), используем выражение (12) и определим коэффициенты Ап(р) таким образом, чтобы решение (12) удовлетворяло бы и неоднородному уравнению (9). Решение, найденное таким образом, обязательно будет удовлетворять и начальным условиям, так как они входят в функцию Ф (х, р) и учитываются поэтому автоматически. Для определения коэффициентов An(р) подставим решение (12) в неоднородное уравнение (9). Учитывая тождество  получим  Используя свойство ортогональности собственных функций2, можем записать  Из этих равенств определяют искомые коэффициенты Ап: 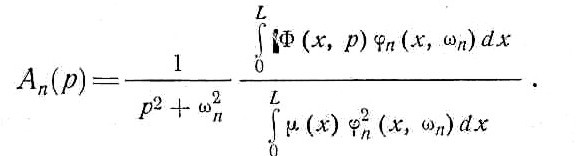 (13)Общим решением уравнения (9) является выражение (12), в котором коэффициенты Ап(р) определяются формулой (13). Таким образом, решение уравнения (9) сводится к задаче отыскания собственных частот и собственных функций, которая является очень сложной. При произвольных зависимостях  эта задача не решается в общем виде и приходится использовать приближенные численные методы.Общее решение уравнения (9) удается получить только в простейших случаях, например, когда балка однородная, т. е.  |