СУЛА. Закон регулирования на работу системы стабилизации (движение крена). В реальных системах переключение рулей отстает на время

• Название: Закон регулирования на работу системы стабилизации (движение крена). В реальных системах переключение рулей отстает на время
• Дата: 19.05.2021
• Размер: 1.09 Mb.
• Имя файла: СУЛА.docx
• Тип: Закон; #207100
• страница: 1 из 8

1. Влияние временного запаздывания и введения производной в закон регулирования на работу системы стабилизации (движение крена).

В реальных системах переключение рулей отстает на время

t  

 arctg



1




e ^  1

_а 135

a 1 

e ^  1

-х_{0 }

В данном случае ^y


1
фазовые траектории сводятся к некоторому придельному циклу независимо от

 0

 0,5



начальных условий в системе существуют автоколебания, определенной амплитуды и частоты.
рассмотрим результат введения первой производной в закон регулирования

dx ² dx dx

Амплитуда колебаний ЛА уменьшается с увеличением ^ ,

^ >1- изменяется режим работы. Этот режим называется скользящим.

2. Оптимальные релейные системы стабилизации (движение крена ) В САМОМ НИЗУ

3. 
   Основные допущения при проектировании САУ статически неустойчивого упругого ЛА.
   

ЛА можно рассматривать как прямую упругую балку (стержень) переменной жесткости с незакрепленными концами. При составлении дифференциального уравнения поперечных колебаний корпуса аппарата, вообще говоря, следует учитывать силы внутреннего неупругого сопротивления и продольные усилия, вызванные тягой двигателя и силой тяжести. Однако для упрощения задачи

d ²

 _d  sign_ (x   _d ) 0

часто принимают, что внутреннее сопротивление отсутствует, и не учитывают продольные усилия. Тогда

sign_

(x  

^dx)  

d

дифференциальное уравнение поперечных колебаний прямой балки записывается в виде:

^dy  y 

d

dx_y d

 0


(1)

Здесь х—координата точки на продольной оси, отсчитанная

переключение рулей происходит, когда:

от носа корпуса летательного аппарата; - прогиб

x   ^dx 0

d

=> уравнение переключения рулей

оси балки в сечении х, измеренный в направлении, перпендикулярном к недеформированной оси балки; -

y ¹ x



в реальных условиях с учетом временного запаздывания

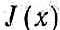
модуль упругости; - момент инерции поперечного

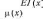
сечения балки относительно нейтральной оси сечения, перпендикулярной к плоскости колебаний; - изгибная жесткость балки в сечении х; - масса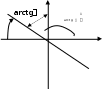

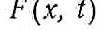
единицы длины балки; - внешняя нагрузка, отнесенная к единице длины балки.

Существенное влияние на упругие колебания летательного аппарата при его полете в плотных слоях атмосферы оказывают аэродинамические силы. Для упрощения задачи часто предполагают, что эти силы не зависят от деформаций аппарата, т. е. определяются только движением соответствующего абсолютно жесткого летательного аппарата. Составляющими силы тяжести, перпендикуляр- ными оси летательного аппарата, обычно пренебрегают.

4. Уравнение поперечных колебаний ЛА и принципы его решения.

Уравнение поперечных колебаний ЛА (с допущениями) совпадает с уравнением прямой балки и записывается в виде:

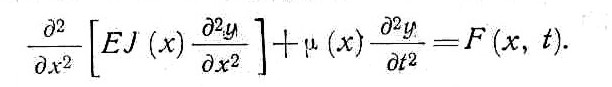
(1)
Здесь х—координата точки на продольной оси, отсчитанная от носа корпуса летательного аппарата;

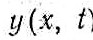
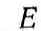
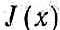
- прогиб оси балки в сечении х, измеренный в направлении, перпендикулярном к недеформированной оси балки; - модуль упругости; - момент инерции поперечного сечения балки относительно нейтральной оси сечения, перпендикулярной к плоскости колебаний;

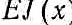
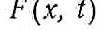
- изгибная жесткость балки в сечении х; - масса единицы длины балки; - внешняя нагрузка, отнесенная к единице длины балки.

Для определения деформации продольной оси аппарата необходимо решить линейное дифференциальное уравнение в частных производных (1), описывающее упругие колебания балки.

При решении уравнения (1) необходимо учитывать как начальные условия, определяющие форму деформированной оси балки в начальный момент времени, так и граничные условия, учитывающие способ закрепления балки. Начальные условия при t=0 имеют вид

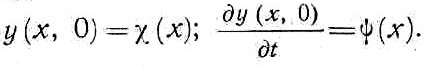
(6)

В нашем случае, когда рассматривается балка со свободными концами, граничные условия имеют следующий вид:

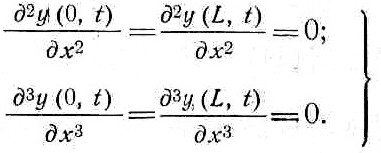
(7)

где L— длина балки, т. е. корпуса летательного аппарата. Эти граничные условия учитывают, что в концевых сечениях балки со свободными концами перерезывающие силы и изгибающие моменты равны нулю.

Так как уравнение (1) является линейным, то его решение находят как сумму решения соответствующего однородного уравнения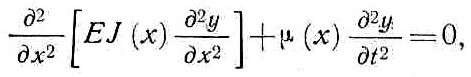



(8)

удовлетворяющего начальным и граничным условиям (6) и (7), и частного решения исходного неоднородного уравнения (1), удовлетворяющего тем же граничным условиям и нулевым начальным условиям.

Решение задачи можно несколько упростить, если, воспользовавшись преобразованием Лапласа, преобразовать по переменной t левую и правую части уравнения (1). Тогда получим уже обыкновенное дифференциальное уравнение, в котором искомая функция у(х, р) зависит от одной независимой переменной х, а переменная р рассматривается как параметр ¹.