Пролетные траектории при межпланетных полетах еще более разнообразны, чем при лунных. Мощные поля тяготения планет юпитерианской группы могут быть эффективно использованы для разгона космических аппаратов до гиперболической гелиоцентрической скорости (что может ускорить полет к более удаленным планетам) и для отбрасывания их к центру Солнечной системы. Речь пойдет о многопланетной траектории (и соответственно о многопланетном перелете) в том случае, когда траектория проходит через сферы действия по крайней мере двух планет, не считая планеты старта.
По сравнению с ПМ в сфере действия Луны можно ввести два существенных упрощения. Время полета внутри сферы действия планеты составляет слишком незначительную часть продолжительности всего перелета, и потому мы можем им пренебрегать. Мы не будем также учитывать изменения величины и направления скорости планеты в течение этого промежутка времени. Это значит, что движение космического аппарата испытывает как бы мгновенный удар со стороны поля тяготения планеты.
Такой подход к
расчету межпланетного ПМ оправдан тем, что при сближении с планетой гелиоцентрическое
движение космического аппарата сначала замедляется, а затем, после облета, убыстряется в ее сфере действия (или наоборот). Так
происходит, например, с Марсом,
который, будучи в начале встречи позади космического аппарата, сначала своим притяжением замедляет его
полет. При полетах к внутренним планетам все, очевидно, происходит
наоборот. В
результате общая продолжительность полета практически не меняется, так что время нахождения в сфере действия планеты можно не учитывать. Существует математическое обоснование
такой методики
.
«Гравитационный
удар» изменяет вектор скорости гелиоцентрического движения. На рис. 7, а, б, в показано соответствующее построение, не нуждающееся в
особых
пояснениях. Следует напомнить, что
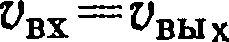
. Заметим, что угол φ поворота вектора плане- тоцентрической скорости за время пролета сферы
действия
целиком зависит
только от величины
входной скорости

(скорости на «местной бесконечности») и от прицельной дальности b:
Из рис. 7, г мы видим, как именно изменился вектор гелиоцентрической скорости за время облета. Это изменение ∆V (показано пунктирной стрелкой) совпадает с приращением ∆v планетоцентрической скорости за время пролета сферы действия. Оно представляет собой тот импульс скорости ∆V,
который притяжение планеты сообщило космическому
аппарату, в
результате чего он изменил свою гелиоцентрическую
орбиту. Если бы планета не обладала притяжением,
необходимая цель
могла бы быть достигнута
только посредством импульса скорости, сообщаемого бортовым ракетным
двигателем.
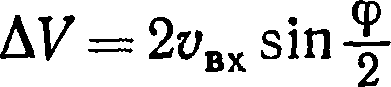
Приращение скорости ∆V, достигнутое в
результате пролета сферы действия планеты, определяется по формуле

(используется
тот факт, что левый треугольник на рис. 7, г равнобедренный,
так
как ).

Чем меньше прицельная дальность, тем сильнее воздействует притяжение планеты на гелиоцентрическую траекторию. При достаточно малой прицельной дальности можно было бы повернуть космический аппарат внутри сферы действия в
сторону, почти противоположную
входу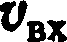
(при
этом ), но прицельная дальность не может быть сделана меньше эффективного радиуса планеты. Поэтому
существуют
максимальный
для
заданного
значения
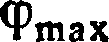
планетоцентрической
входной скорости угол
поворота
планетоцентрической
скорости ,
который определяется
формуллой
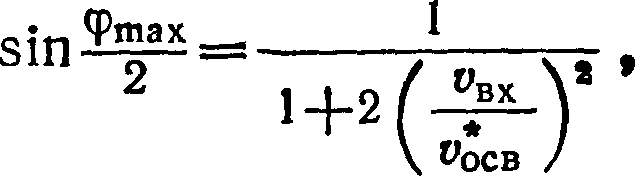
и соответствующее ему максимальное приращение скорости
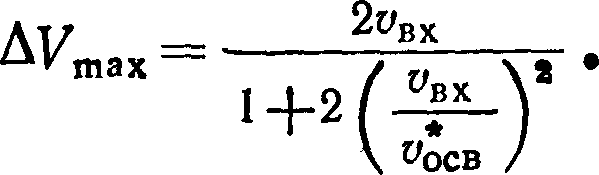
Им отвечает траектория, проходящая у самой поверхности планеты или у кромки ее атмосферы.
 Скачать 1.09 Mb.
Скачать 1.09 Mb.