СУЛА. Закон регулирования на работу системы стабилизации (движение крена). В реальных системах переключение рулей отстает на время

• Название: Закон регулирования на работу системы стабилизации (движение крена). В реальных системах переключение рулей отстает на время
• Дата: 19.05.2021
• Размер: 1.09 Mb.
• Имя файла: СУЛА.docx
• Тип: Закон; #207100
• страница: 3 из 8

Импульсные маневры космического ЛА в центральном гравитационном поле.

Простейшим видом импульсного перехода КА на новую орбиту является _{ОДНОИМПУЛЬСНЫЙ ПЕРЕХОД}. Такой переход возможен лишь в том случае, когда начальная и требуемая орбит» имеют общую точку. Импульс, прикладываемый в этой точке рассчитывают таким

образом, чтобы векторная сумма орбитальной скорости на исходной орбите и импульса скорости AM равнялась вектору , соответствующему

скорости аппарата в рассматриваемой точке на новой орбите. Одной из простейших задач компланарного маневра является задача определения требуемо го приращения скорости для перевода КА с круговой орбиты на эллиптическую, ориентированную определенным образом относительно начального положения, задаваемого точкой схода. Выражения для радиальной и трансверсальной составляющих скорости КА, движущегося по эллиптической орбите, запишем в виде




Скорость КА на начальной круговой орбите радиуса r_н (рис. 10.4)

определяют как ,тогда и ,следовательно,




Разделив правую и левую части уравнения (10.49) на V% , получим



Безразмерное отношение 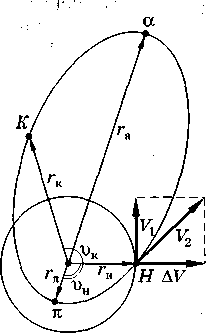представляет собой меру количества энергии, которую необходимо сообщить КА для перевода его с опорной круговой орбиты на эллиптическую, проходящую через заданную точку К.


Рис. 10.4. Схема перехода с круговой на заданную эллиптическую орбиту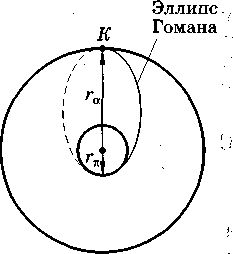




Рис. 10.5. Схема гомановского перехода КА между компланарными круговыми орбитами

Наиболее характерным и распространенным видом ДВУХИМПУЛЬСНОГО ПЕРЕХОДА является упоминавшийся ранее переход между компланарными круговыми орбитами по траектории касательного полуэллипса тангенциального маневра, линия апсид которого включает в себя радиусы круговых орбит (рис. 10.5). Переход, основанный на реализации указанной траектории, называют моноэллиптическим переходом Гомана. Переходную траекторию Гомана также часто называют полуэллипсом минимальной энергии.

Импульсное изменение скорости при выполнении маневра осуществляется в перигее и апогее переходной орбиты. Скорость, которую КА будет иметь на внутренней круговой орбите, представим как


Скорость же, требуемую для достижения внешней орбиты, рас считывают по формуле


Тогда разность скоростей и дает значение необходимого приращения , Именно такую скорость

необходимо сообщит!. аппарату, чтобы он вышел на траекторию перелета:


На основании выражения интеграла площадей

имеет

место равенство





Таким образом, для того чтобы КА начал двигаться по внешней орбите, в точке К необходимо приложить второй импульс скорости, равный

При переходе на внутреннюю орбиту с внешней круговой орбиты оба импульса должны быть направлены в сторону уменьшения местной орбитальной скорости. Расчет их требуемых значений может быть выполнен по формулам



Так как точка старта с исходной орбиты диаметрально противоположна точке прибытия на орбиту назначения, то положение начальной точки переходной траектории определяется требуемым положением конечной точки.

Полный импульс, который необходимо приложить в точка* Н и К для реализации перелета по схеме Гомана, равен


Единственный положительный корень

итого уравнения соответствует .

При указанном знамении отношения радиусов требуемые энергетические затраты достигают максимального значения. Причем можно показать, что ^{при двухимпульсный переход перестает} быть абсолютно оптимальным по требуемым затратам топлива и что существует энергетически более выгодный БИЭЛЛИПТИЧЕСКИЙ ТРЕХИМПУЛЬСНЫЙ ПЕРЕХОД .
Рис. 10.6. Девять основных типов эллиптических гелиоцентрических орбит перелета

Каждому типу эллиптических орбит перехода «в один конец» обычно присваивают номер — однозначное число (например, «0» для гомановского перелета), а каждой траектории перелета с возвращением — двузначное число (например, «00» для гомановской траектории облета). При этом в случае перелета с возвращением первая цифра двузначного номера соответствует номеру

одностороннего перелета от Земли к планете-цели, а вторая цифра означает номер одностороннего перехода от планеты-цели к Земле (возвращение). Если же при перелете с возвращением используют гиперболический переход, то их номера записывают последовательно через запятую, начиная с орбиты полета от Земли и кончая орбитой возвращения.
Рис. 10.7. Три основных типа гиперболических орбит перелета

Некомпланарность начальной и конечной орбит приводит к естественному увеличению затрат характеристической

скорости на выполнение маневра по сравнению с компланарным случаем. Сколь-нибудь завершенной общей теории оптимальных импульсных программ пространственного маневра не существует. Решения ищут обычно в каждом конкретном случае с учетом граничных условий и целевого назначения полета.

6. 
   Межпланетные перелёты ЛА.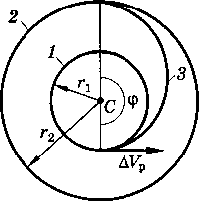
   

Факт постоянства планетарных орбит позволяет предположить, что

возможно такое взаимное расположение планеты старта 1 и планеты цели 2, когда осуществление полета потребует наименьших затрат энергии.

Ограничимся рассмотрением простейшего случая: пренебрежем эллиптичностью орбит и их наклонение к плоскости эклиптики, т. е. будем считать, что орбиты планет являются круговыми и лежат в одной плоскости. Так как рассматривается только центральная сила притяжения Солнца, то задачу оценочного проектно-баллистического расчета траектории полета КА от одной планеты к другой можем рассматривать как задачу невозмущенного движения.

На рис. показана схема перелета с внутренней планеты, движущейся по круговой орбите с величиной радиуса r1 на внешнюю с радиусом орбиты r2. Энергетически оптимальной траекторией в рамках данной постановки задачи, обеспечивающей перевод КА с орбиты 1 на орбиту 2

, является траектория, касательная к исходным орбитам при угле перелета φ = 180° и с большой полуосью . Это так называемый оптимальный романовский эллипс.

При полете по такой траектории КА должен иметь в начальный момент следующее значение скорости относительно Солнца (используем формулу

), в которую подставим значения радиусов r1 и r2

соответствии с рис.):


(2.1)

где µс — произведение постоянной тяготения на массу Солнца. Так как КА движется вместе с планетой, то для перевода КА на траекторию межпланетного перелета его надо разогнать относительно планеты старта 1 до скорости, называемой скоростью на бесконечности ( ) которая определяет энергетику, необходимую для

реализации перелета (здесь 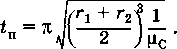— скорость планеты старта относительно Солнца). Все рассуждения справедливы и для перелетов с внешней планеты на внутреннюю (например, с орбиты Земли на орбиту Венеры), но при этом КА надо затормозить относительно планеты старта.

Рассмотрим вопрос о времени, необходимом для перелета с орбиты 1 на орбиту 2. Очевидно, что время tn равно полупериоду обращения КА по орбите перелета:


(2.2)

Для обеспечения встречи КА с планетой назначения необходимо, чтобы в момент касания орбиты перелета с орбитой планеты назначения аппарат и планета находились в одной и той же точке. Рассмотрим, каким должно быть

расположение планет в момент отлета КА с орбиты 1, чтобы после истечения времени tп обеспечивалось условие встречи КА с планетой назначения 2.

Согласно интегралам площадей при движении в центральном поле тяготения радиусы-векторы планет

«ометают» в равные промежутки времени равные площади. Поскольку КА и планета назначения движутся по различным орбитам, то их угловое перемещение за время tп будет различным. Так как рассматриваются круговые орбиты, то за время tп планета назначения переместится на

угол , где п — средняя угловая скорость

движения по орбите . Подставив значения п и tп в формулу для φ2, получим

(2.3)
где

За время tn КА перемещается на угловое расстояние, равное π, и таким образом в начальный момент планета старта 1 и планета назначения 2 должны занимать положение, при котором угол между радиусами-векторами r1 и r2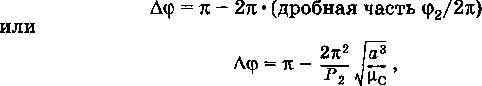


где Рг — период обращения планеты 2. В случае ∆φ > 0 планета назначения опережает планету старта, при ∆φ < 0

• 
  отстает от нее. Поэтому реализация энергетически оптимальных траекторий перелета возможна лишь при строго определенном взаимном расположении планет. Любое отклонение от этого расположения вызывает увеличение потребной для перелета энергетики.
  

Так как реализация оптимальных полетов с Земли к другим планетам требует строго определенного расположения планеты относительно Земли, то, естественно, повторяемость этой конфигурации будет наступать через синодический период.