ПЗ № 1 Формализация ЗЛП и ГМ ее решения. Занятие 1 Построение математических моделей задачи линейного программирования Пример решения задачи

• Название: Занятие 1 Построение математических моделей задачи линейного программирования Пример решения задачи
• Дата: 08.10.2020
• Размер: 489.5 Kb.
• Имя файла: ПЗ № 1 Формализация ЗЛП и ГМ ее решения.doc
• Тип: Занятие; #141684
• страница: 1 из 6

Практическое занятие №1

Построение математических моделей

задачи линейного программирования

1. 
   Пример решения задачи
   

Для обеспечения эффективного решения поставленных задач на пункте управления планируется организовать 2 независимых направления связи, каждое из которых сможет обеспечить каналы связи для передачи данных и каналы спутниковой связи. Для организации первого направления связи выделено: - тыс. рублей. Для организации второго направления связи выделено: - тыс. рублей.

Расходы на организацию и эксплуатацию одного канала связи передачи данных и одного канала спутниковой связи по соответствующим направлениям связи при этом составят (табл. 1)

Таблица 1

	Первое направление	Второе направление
Передача данных	тыс.руб	тыс.руб
Спутниковая связь	тыс.руб	тыс.руб

Эффективность управления, при наличии на пункте управления одного канала передачи данных составит условных единиц, одного канала спутниковой связи – условных единиц.

Требуется: определить, сколько каналов связи целесообразно организовать, чтобы эффективность управления была максимальной.

Решение

1. Формализуем заданные условия задачи.

Введем переменные: x₁ – оптимальное количество каналов передачи данных организуемых в направлениях связи, x₂ – оптимальное количество каналов космической связи организуемых в направлениях связи.

Обозначим W(x) – максимальная эффективность управления после организации двух направлений связи.

По результатам формализации имеет место задача линейного программирования:

а) условия-ограничения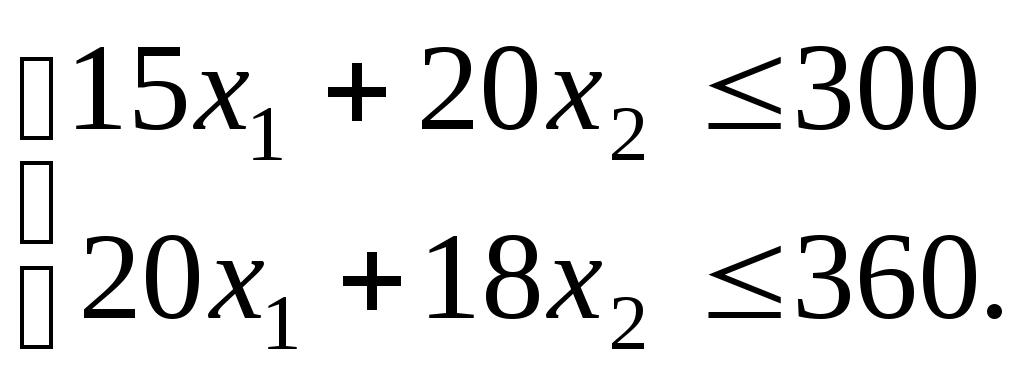

(1)

б) целевая функция - W(x) = 0,5x₁+0,6x₂ → max (2)

2. Решим для наглядности задачу линейного программирования геометрическим методом. Решение задачи представлено на рисунке 1

Обозначим на графике результат решения задачи – W₁(x)max, затем сравним полученный результат с результатом решения поставленной задачи табличным симплекс-методом – W₂(x)max с применением ППП Excel.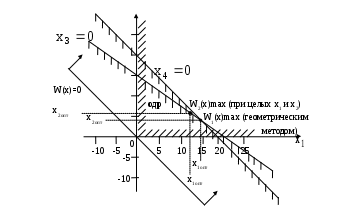

Рисунок 1 – Решение задачи линейного программирования на плоскости

W₁(x)max ≈ , окончательно W₁(x)max ≈ .

2. 
   Запишите экономико-математическую модель для следующих задач
   

1. Известно, что содержание трех питательных веществ А, В и С в рационе должно быть не менее 80, 60 и 30 единиц соот­ветственно. Указанные питательные вещества содержат три вида продуктов. Содержание единиц питательных веществ в одном килограмме каждого из видов продуктов приведено в таблице.

Питательные вещества	Количество единиц питательных веществ
	I	II	III
А	1	4	3
В	2	4	2
С	2	1	3
Цена 1 кг продукта	10	12	8

Определите дневной рацион, обеспечивающий получение не­обходимого количества питательных веществ, при минимальных денежных затратах.

2. Торговое предприятие реализует 4 группы товаров (А, В, С и D). Нормы затрат ресурсов на каждый тип товаров, лимиты ресурсов, а также доход на единицу каждой продукции заданы в таблице. Определить плановый объем продаж и струк­туру товарооборота так, чтобы доход торгового предприятия был максимален.

Виды ресурсов	Норма затрат ресурсов на 1 ед. товара				Лимит ресурсов
	Группа А	Группа В	Группа С	Группа D
Рабочее время про­давцов, чел.-час.	0,2	1,2	3	0,8	1400
Площадь торговых залов, м2	0,5	0,2	0,1	0,05	200
Площадь складских помещений, м2	3	0,5	1	2	1000
Накладные рас­ходы, руб.	5	7	4	8	800
Доход на ед. про­дукции, руб.	4	5	3	4

3. Предприятие может работать по пяти технологическим процессам (Т₁, Т₂, Т₃, Т₄ и Т₅), причем количество единиц вы­пускаемой продукции по разным технологическим процессам за 1 ед. времени соответственно равно 300, 260, 320, 400 и 450 шт. В процессе производства учитываются следующие факторы: сырье, электроэнергия, зарплата и накладные расходы. Затраты соответствующих факторов при работе по разным технологиче­ским процессам в течение 1 ед. времени указаны в нижеследую­щей таблице.

Производственные факторы	Затраты при различных технологиях					Лимит
	Т1	Т2	Т3	Т4	Т5
Сырье	15	18	12	14	20	5000
Электроэнергия	0,2	0,3	0,25	0,15	0,25	400
Оплата труда	60	50	80	60	70	16 000
Накладные расходы	15	18	20	10	19	10 000

Найти программу максимального выпуска продукции.

4. Ресторан "Охотник" обслуживает обедами близлежащие коммерческие предприятия, приготавливая первые и вторые блюда.

Известны затраты на производство, доставку, накладные расхо­ды производства и товарооборот для каждого блюда, см. таблицу. Плановый фонд ресурсов следующий: затраты на производство не должны превышать 850 чел.-час; на доставку потребителям – 1200 чел.-час; накладные расходы должны быть не более 2100 руб. и план товарооборота 5800 руб. Известна также доля дохода от каждого блюда.

Требуется найти, какое количество каждого вида блюд надо выпускать при заданных ограничениях, чтобы обеспечить мак­симум дохода ресторана.

Ресурсы	Нормы затрат ресурсов на 100 блюд
	1-е блюдо	2-е мясное	2-е рыбное	2-е овощное	прочее
Затраты труда на про­изводство, чел.-час	3,4	5	38	2,6	23
Затраты труда на доставку, чел.-час	2,1	5,2	5,1	2,8	3
Накладные расходы, руб.	6,4	8,5	8,4	10	6,1
Товарооборот, руб.	25	37	23	22	20
Доход, руб.	1,5	3,0	5,4	0,8	1,2

5. Издательский дом "ОНИКС" издает три журнала: "Сделай сам", "Дом в деревне" и "Садовник", которые печата­ются в трех типографиях: "Типография № 1", "Полиграф" и "АПН", где общее количество часов, отведенное для печати, и производительность печати одной тысячи экземпляров огра­ничены и представлены в таблице.

Спрос на журнал "Сделай сам" составляет 15 тыс. экз., на "Дом в деревне" – 8,5 тыс. экз., а на журнал "Садовник" – не более 18 тыс. экз. в месяц.

Определите оптимальное количество издаваемых журналов, которые обеспечат максимальную выручку от продажи.Типография	Время печати 1000 экз.			Ресурс времени, отведенный ти­пографией, час
	"Сделай сам"	"Дом в деревне"	"Садовник "
Типография № 1	6	12	8	142
Полиграф	4	6	9	94
АПН	8	4	6	70
Оптовая цена, руб./шт.	20	25	28