История математики 4ФиМ ИПР Кулакова Ю.В.. Зарождение математики переменных величин. Декарт, Ферма, Кеплер, Кавальери, Паскаль и другие
 Скачать 284.13 Kb.
|
|
1. Основные достижения математики 17 веке. 1.1 Открытие логарифмов Математические достижения 17 в. начинаются открытием логарифмов. Некоторые математики 16 в. в известной мере занимались сопоставлением арифметической и геометрической прогрессий, главным образом с целью облегчить работу со сложными тригонометрическими таблицами. Важным достижением на этом пути мы обязаны лорду Джону Неперу (1550-1617), который в 1614 г. напечатал свое «Описание удивительного канона логарифмов». Основной идея в построении логарифмов связана с рассмотрением двух последовательностей чисел. 0,1, 2 ,3 ,4,.... 1,a,a2,a3,a4,... Произведение любых двух членов второй последовательности является членом той же последовательности, получаемым путем возведения a в степень, равную сумме соответствующих членов первой последовательности. Эта идея была четко выражена еще в «Исчислении песчинок» Архимеда. Сопоставлением этих последовательностей пользовались Шюке, Пачоли и др. Штифель продолжил эти ряды и влево, т.е. включил и отрицательные числа и впервые называет члены первого ряда экспонентами, т.е. показателями соответствующих членов второго ряда. В 1619 году, после смерти автора, опубликовано «Построение удивительной таблицы логарифмов», где объясняется принцип логарифмических таблиц, помещенных в первой книге. Однако, по-видимому, уже к 1594 г. Непер владел принципом образования логарифмов. Независимо от Непера в 1629 г. аналогичные, хотя менее совершенные таблицы логарифмов составил швейцарский математик Иобст Бюрги (1552-1632) в книге «Таблицы арифметической и геометрической прогрессий». Бюрги помогал Кеплеру в астрономических вычислениях. Для того, чтобы, опираясь на сопоставление прогрессий, перейти к составлению таблицы, перед Бюрги стояли две задачи. Первая: сделать так, чтобы ряд (2) охватил по возможности больше чисел. Если взять, например, основание 2, то можно получить логарифмы для довольно «редкого» ряда чисел. Для практических вычислений таблица логарифмов только этих чисел далеко не достаточна. Нетрудно заметить, что чем ближе основание будет ближе к 1, тем больше чисел будет охвачено таблицей. В качестве основания Бюрги взял 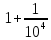 Неявно предполагая непрерывность соответствия между рядами чисел (1) и (2), он применил к своей таблице интерполяцию. Вторая задача, стоявшая перед Бюрги, заключалась в следующем: при последовательных умножения число знаков произведений быстро растет, сохранять их все практически невозможно. Округление, однако, следует вести крайне внимательно, для того чтобы при дальнейших вычислениях не накопились ошибки. Бюрги констатировал, что чем «плотнее» второй ряд, тем меньше погрешность в вычислениях. Фактически он составил таблицу чисел 108(1,0001)n , придавая n последовательно значения 10, 20, 30, … Т.о. Бюрги рассматривал ряды 0, 10, 20, 108,108(10,0001),108(10,0001)2,... Числа первого ряда («черные») он вычислил с 9 знаками и довел до 109 - это «полное черное» число. Ему соответствует «полное красное» число 230270022. Бюрги отдал составлению таблиц восемь лет жизни. Одних умножений на 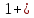 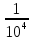 пришлось произвести 200 млн. раз.Таблицы, составленные Непером, отличаются во многом от таблиц Бюрги. Непер было построил две последовательностей чисел, связанных таким образом, что когда одна из них возрастает в арифметической прогрессии, другая убывает в геометрической. Знаменатель прогрессии равен 1 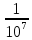 , он ближе к 1, чем в последовательности Бюрги. Такая медленно убывающая прогрессия дает возможность включить в таблицу большее количество чисел, сравнительно мало отличающихся друг от друга. Для того чтобы для любого положительного числа вычислить его логарифм, Непер сформулировал идею непрерывности связи между числами и их логарифмами.Пусть на осях Ох и О’у движутся соответственно точки А, В, выходящие с одинаковой скоростью с, и пусть на оси О’у зафиксирована некоторая точка К. Движение точки А равномерное, для нее скорость с постоянная. Скорость замедленно движущейся точки В непрерывно убывает пропорционально расстоянию y BK . Какое расстояние ей остается еще пройти до точки К? За некоторый промежуток времени одновременно вышедшие точки проходят неодинаковые расстояния x1 y1. Для другого промежутка времени x2 y2. Можно доказать, что, при x2 x1 x4 x3 будем иметь 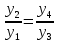 ,т.е. при одинаковой разности двух любых значений чисел х получим одинаковое отношение двух соответствующих значений чисел у. Числа х - логарифмы – как бы определяют отношения соответствующих чисел у. Общий членарифметической прогрессии таблицы Непера можно представить в виде n(10,5107 . Составлению таблицы Непер посвятил около 20 лет своей жизни. Идея о непрерывности, заложенная Непером при составлению таблиц, является зародышем развившихся после него глубоких идей исчисления бесконечно малых. Непер составил таблицы для тригонометрических вычислений, а для других расчетов они были неудобны. В 1624 г. Генри Бригс улучшил логарифмы. Он опубликовал «Логарифмическую арифметику», в которой содержались таблицы десятичных логарифмов. Простота в вычислениях с помощью десятичных логарифмов вытеснила таблицы, предложенные Непером. |