История математики 4ФиМ ИПР Кулакова Ю.В.. Зарождение математики переменных величин. Декарт, Ферма, Кеплер, Кавальери, Паскаль и другие
 Скачать 284.13 Kb. Скачать 284.13 Kb.
|
|
Становление математического анализа. Итак, к 80-м годам 17 в. задачи вычисления площадей, объемов, координат центров тяжести и т.д. достигли уже определенного уровня развития. Хотя новых исчислений еще не было, имелись такие результаты, которые в силу своей общности и автоматичности своего получения были составной частью некоего неизвестного еще исчисления. Таков, например, результат 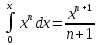 значение, которого тем больше, что он получен независимо несколькими математиками. Не меньшим вниманием пользовались задачи на касательные, на отыскание максимума и минимума. И здесь еще не было исчисления, но были уже методы, вполне устойчивые и общие. В частности, вырисовывалось основополагающее значение выражения задач. f( x e)f( x) e для этой категории Наконец, к указанному времени установлена взаимная зависимость двух важнейших операций: вычисления квадратуры кривой и отыскания касательной, проведенной через данную точку кривой. Осталось объединить все эти результаты и создать цельный алгоритм, обнимающий совокупность входящих в эту область математики вопросов. Решение этой задачи пришлось на последние 15 лет 17 в. и на 18 в. Среди лиц, которым выпало на долю решить эту историческую задачу, на первом месте стоит англичанин Исаак Ньютон. Как все великие люди того времени, он не был специалистом лишь в одной отрасли науки. Математик, механик, оптик и астроном, он оказал глубокое влияние на развитие всех точных наук, которые в его время еще не сформировались и не выделились из одной «пра-науки» - натуральной философии. Обладая чрезвычайно мощным умом, Ньютон в студенческие годы (1661-1665) овладел всем существенным, что было достигнуто к тому времени в математике, т.е., помимо трудов древних и средневековых авторов, также «Геометрией» Декарта, результатами Ферма, достижениями итальянцев (Кавальери, Торричелли) и англичан (Валлис, Барроу) и многих других. В течение вынужденного двухлетнего пребывания в деревне (1665-1667) Ньютон заложил основы высшей математики, физической оптики и небесной механики. Для Ньютона математика не была абстрактным детищем человеческого ума. После некоторых колебаний он пришел к воззрению на геометрический образ (линия, поверхность, объем) как на результат движения точки, линии или поверхности; движение происходит во времени и за сколь угодно малое время точкой проходится сколь угодно малый путь. Вот этот-то малый путь и приводит к малому приращению линии или чего- нибудь другого, а отношение этого малого приращения пути к малому времени, за которое этот малый путь пройден, дает скорость. Чтобы получить мгновенную скорость, надо перейти к пределу, т.е. взять «последнее отношение». Толкование физического содержания описанного процесса у Ньютона мало менялось, но это не мешало выработке формального аппарата. Так получилось, что Ньютон пришел к необходимости находить «последние отношения», т.е., по современной терминологии, искать пределы отношений приращения функции к приращению времени. При желании, разумеется, можно вычислить предел отношения приращения одной функции времени к приращению другой функции, т.е. вычислить производную функции по ее аргументу. Широко и свободно пользуясь теоремой Торричелли-Барроу о взаимности операций дифференцирования и интегрирования и располагая производными многих функций, Ньютон легко нашел квадратуры многих кривых. В тех же случаях, когда интеграл данной функции найти было нельзя, Ньютон разлагал подынтегральную функцию в степенной ряд и почленно его интегрировал. Искусство разложения функции в ряд само есть детище Ньютона. Для выполнения разложения Ньютон пользовался разными приемами, из которых на первое место следует поставить использование формулы бинома, но применялось и деление типа1 |
