Зміст модуль I. Основи інформаційних технологій в системі охорони здоровя. Обробка та аналіз медикобіологічних даних 4
 Скачать 4.71 Mb. Скачать 4.71 Mb.
|
Клінічні системи підтримки прийняття рішень. Засоби прогнозування. Моделювання системи підтримки прийняття рішеньІнформаційні технології апроксимації та прогнозу статистичних даних. Підтримка прийняття рішень за допомогою простих засобів прогнозування.Конкретні цілі заняття: демонструвати вміння функціональної апроксимації даних і побудови простих прогнозів засобами електронних таблиць. Основні поняття теми Функціональна апроксимація, лінія тренда, тип лінії тренда, аналітичне представлення експериментальних даних, задача апроксимації, ступінь наближення, точність даних, комп’ютерна технологія апроксимації експериментальних даних. Короткі теоретичні відомостіПоняття апроксимації статистичних даних На практиці часто доводиться зустрічатися із задачею апроксимації. Апроксимацією називається процес підбору емпіричної формули (х) для встановленої з досвіду функціональної залежності у= f(х). Емпіричні формули використовують для аналітичного подання експериментальних даних. Сформулюємо задачу функціональної апроксимації для випадку однієї незалежної змінної. Нехай є деякі дані, отримані практичним шляхом (під час експерименту, спостереження тощо), які можна представити парами чисел (х; у). На основі цих даних потрібно підібрати функцію у = (х), яка щонайкраще згладжувала б експериментальну залежність між змінними х і у й по можливості точно відбивала загальну тенденцію залежності між ними. Звичайно задача апроксимації розпадається на дві частини. Спочатку встановлюють вид залежності у = f(х) і, відповідно, вид емпіричної формули (лінійна, квадратична, логарифмічна тощо). Після цього визначаються чисельні значення невідомих параметрів обраної емпіричної формули, для яких наближення до заданої функції виявляється найкращим. При відсутності теоретичних міркувань при підборі виду формули, зазвичай вибирають функціональну залежність з числа відомих, порівнюючи їхні графіки із графіком заданої функції. Після вибору виду формули визначають її параметри. Для найкращого вибору параметрів задають міру наближення апроксимації експериментальних даних. У багатьох випадках, особливо якщо функція f(х) задана графіком або таблицею (на дискретній множині точок), для оцінки ступеня наближення розглядають різниці f(х) - (х) для точок хо, х1, ..., хк. Існують різні ступені наближення й, відповідно, методи розв’язання цієї задачі, зокрема метод найменших квадратів. При цьому функція (х) вважається найкращим наближенням до f(х), якщо для неї сума квадратів відхилень (хі) від відповідних значень f(xі),  має найменше значення в порівнянні з іншими функціями, з числа яких вибирається шукане наближення. З’ясувати вид функції можна або з теоретичних міркувань, або аналізуючи розташування точок (хn; уn;) на координатній площині. Наприклад, нехай точки розташовані так, як показано на рис. 57.  Рис. 51. Можливий варіант розташування експериментальних точок Зважаючи на те, що практичні дані отримані з деякою похибкою, зумовленою неточністю вимірів, необхідністю округлення результатів тощо, природно припустити, що залежність між хn та уn є обернено пропорційна й функцію (х) потрібно підбирати у вигляді Комп’ютерна технологія апроксимації експериментальних даних Розглянемо апроксимацію експериментальних даних засобами електронних таблиць МS Ехсеl. В середовищі електронних таблиць апроксимація здійснюється шляхом побудови графіка експериментальних даних з наступним підбором апроксимуючої функції (лінії тренда). Можливі наступні типи ліній тренда: 1. Лінійна у = ах + b. Як правило, лінійною функцією апроксимуються експериментальні дані, які зростають або спадають із постійною швидкістю. 2. Поліноміальна у= а0 + а1х + а2х2 +... + аnxn. Використовується для опису експериментальних даних, по черзі зростаючих і спадаючих. Степінь полінома визначається кількістю екстремумів (максимумів або мінімумів) кривої. Поліном другого степеня може описати тільки один максимум або мінімум, поліном третього степеня може мати один або два екстремуми, четвертого степеня – не більше трьох тощо. 3. Логарифмічна 4. Степенева у = bxn, де а й b – константи. Апроксимація степеневою функцією використовується для експериментальних даних, які незмінно зростають або спадають. Дані не повинні мати нульові або від’ємні значення. 5. Експонентна у = bеax, де а, b – константи, е – основа натурального логарифма. Функція застосовується для опису експериментальних даних, які швидко зростають (спадають), а потім поступово стабілізуються. Часто використання експоненти випливає з теоретичних міркувань. Степінь наближення апроксимації експериментальних даних вибраною функцією оцінюється коефіцієнтом детермінації R2. Таким чином, якщо маємо декілька придатних варіантів типів апроксимуючої функції, можна вибрати функцію з більшим коефіцієнтом детермінації (ближчим до 1). Для здійснення апроксимації на діаграмі експериментальних даних необхідно клацанням правої кнопки миші викликати контекстне меню, і вибрати пункт Добавить линию тренда. У діалоговому вікні Линия тренда (рис. 53) на вкладці Тип задається тип апроксимуючої функції, а на вкладці Параметры – додаткові параметри, які впливають на відображення апроксимуючої кривої. Демонстраційний приклад 1Дослідимо характер зміни з часом приросту населення (на 1000 чол.) в місті N та підберемо апроксимуючу функцію, маючи наступні дані:
Для побудови діаграми, передусім, введемо дані в електронну таблицю (рис. 52). За введеними даними будуємо діаграму. Оскільки, зміна приросту населення подано за однакові проміжки часу – вибираємо діаграму Графік. 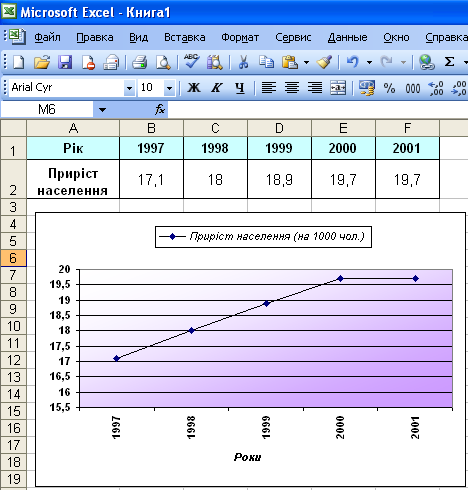 Рис. 52. Введення даних в електронну таблицю та побудова діаграми (графіка) Клацанням вказівником миші на панелі інструментів викликаємо Майстер діаграм. В діалоговому вікні, що з’явилося вибираємо тип діаграми Графік, вид – графік з маркерами. Після натиснення кнопки Далее вказуємо за допомогою миші діапазон даних – В1:В6. Перевіримо положення перемикача Ряды в: строках. Вибираємо вкладку Ряд і з допомогою мишки вводимо діапазон підписів осі Х: А2:А6, та ім’я ряду даних – Приріст населення на 1000 чол. Натиснувши кнопку Далее, вводимо підпис осі Х – Роки і натискаємо кнопку Готово. Отримали графік експериментальних даних (рис. 52). Апроксимуємо отриману криву поліноміальною функцією другого порядку, оскільки крива досить гладка і не дуже відрізняється від прямої лінії. Для цього викликаємо контекстне меню графіка, в якому вибираємо пункт Добавить линию тренда. В діалоговому вікні, що з’явилося, Лінія тренда (рис.53) на вкладці Тип вибираємо тип лінії тренда – Поліноміальна і встановлюємо степінь – 2. Потім відкриваємо вкладку Параметры (рис. 53) і встановлюємо прапорці в поля показывать уравнения на диаграмме та поместить на диаграмму величину достоверности аппроксимации (R^2), після чого натискаємо на кнопку ОК. 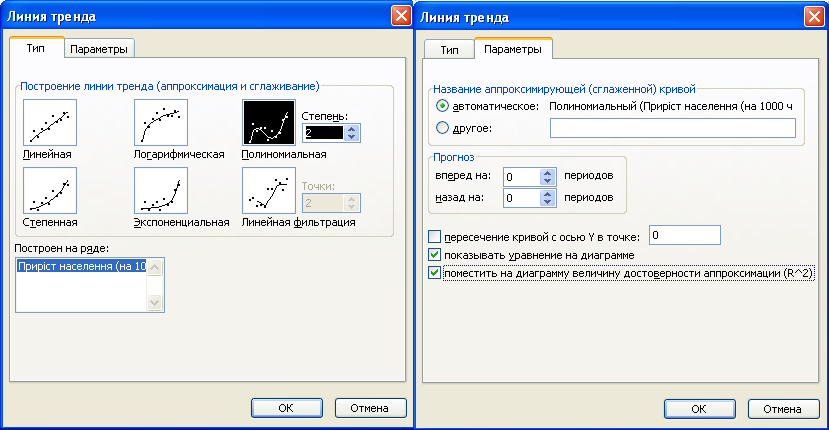 Рис. 53. Вкладки діалогового вікна Линия тренда В результаті отримуємо апроксимуючу криву (рис. 54). 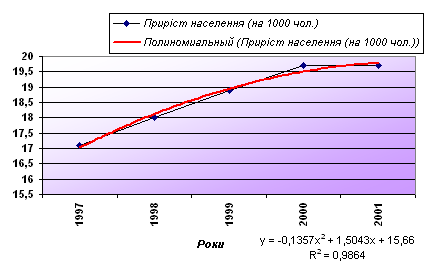 Рис. 54. Експериментальні дані, апроксимовані поліноміальною кривою Як видно з рисунка 54, рівняння поліноміальної апроксимуючої функції для деяких значень х (1, 2, 3,…) має вигляд у = -0,1357х2+1,5043х+15,66. При цьому точність апроксимації досить висока R2= 0,986. Спробуємо покращити якість апроксимації вибором іншого типу функції (можливо, більш адекватного). В даному випадку допустимим варіантом може бути логарифмічна функція. Для цього аналогічно до описаного вище апроксимуємо дані логарифмічною кривою (тип лінії тренду – Логарифмическая). В результаті маємо інший варіант апроксимації (рис. 55). 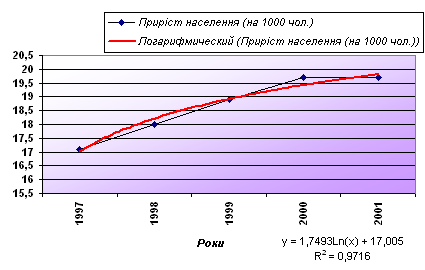 Рис. 55. Експериментальні дані, апроксимовані логарифмічною кривою Проаналізувавши рисунок 55, стверджуємо, що рівняння логарифмічної апроксимуючої кривої поступається в точності апроксимації поліноміальної кривої – R2 = 0,9716 < 0,986. Тому, за відсутності будь - яких теоретичних міркувань, можна вважати, що найкращою апроксимацією є апроксимація поліноміальною функцією другого степеня (з двох розглянутих варіантів). Демонстраційний приклад 2Після викиду ядовитої речовини його концентрація (мг/л) у водоймищі змінювалась у відповідності з наступною таблицею:
Визначимо тип функціональної залежності зміни концентрації речовини з часом і оцінимо її концентрацію в момент викиду. Для цього введемо дані в електронну таблицю та побудуємо діаграму. Оскільки необхідно будувати динаміку зміни концентрації речовини відповідно з вказаними проміжками часу (нерівномірними) – будуємо діаграму Точечная (рис. 56). Апроксимуємо отриману криву. Оскільки крива візуально походить на експоненту і з теоретичних міркувань ймовірніше, що закон зміни – експоненціальний, доцільно апроксимувати криву зміни концентрації експоненціальною функцією. Для цього викликаємо контекстне меню графіка, в якому вибираємо пункт Добавить линию тренда. В діалоговому вікні, що з’явилося, Лінія тренда на вкладці Тип вибираємо тип лінії тренда – Експоненціальна. Потім відкриваємо вкладку Параметры і встановлюємо прапорці в поля показывать уравнения на диаграмме та поместить на диаграмму величину достоверности аппроксимации (R^2). Крім цього, для того щоб оцінити концентрацію речовини у водоймищі в момент викиду, в полі Прогноз назад на встановлюємо 1 периодов. Після чого натискаємо кнопку ОК. В результаті отримуємо апроксимуючу криву (рис. 57). Як видно з рисунка 57, рівняння експонентної апроксимуючої функції для залежності концентрації від часу має вигляд у = 11,844е-0,4695. При цьому точність апроксимації досить висока R2= 0,9951,що дозволяє вважати опис процесу зміни концентрації речовини у водоймищі експоненціальною функцією адекватним. Розрахункова оцінка концентрації речовини в момент викиду, як видно з графіка, становить близько 12 мг/л. Точнішу цифру отримуємо з рівняння у = 11,844е-0,4695 при х = 0 (у0 = 11,84 мг/л). 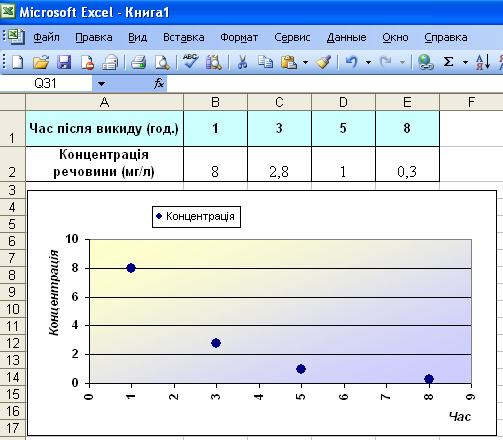 Рис. 56. Введення даних в електронну таблицю та побудова точкової діаграми 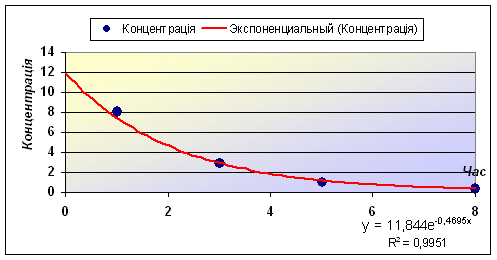 Рис. 57. Експериментальні дані, апроксимовані експонентною кривою Практичні завдання Завдання 1. Візуалізація медико-статистичних даних (за допомогою діаграми). Побудуйте діаграму залежності кількості захворілих від часу на основі статистичних даних розвитку епідемії (табл. 25). Таблиця 25. Статистичні дані розвитку епідемії
Вказівки до виконання завдання 1). Заповніть даними робочий лист електронної таблиці. 2). Для побудови діаграми скористайтеся схемою 2. Відредагуйте діаграму таким чином, щоб крок по часу відповідав 5 діб. Для цього скористайтеся схемою 3. Завдання 2. Побудова прогнозу розвитку епідемії Виконайте функціональну апроксимацію статистичних даних розвитку епідемії за даними таблиці 25. Вказівки до виконання завдання 1) Апроксимуйте отриману криву за допомогою степової функції. Рівняння та величину достовірності апроксимації покажіть на діаграмі. Для побудови функції прогнозу та встановлення відповідних параметрів скористайтеся схемою 4. 2) Визначити на основі отриманої аналітичної залежності кількість захворілих на 10 тис. населення на 11, 13, 15 день від початку розвитку епідемії. 3) Визначити, у який день кількість захворілих на 10 тис. населення перевищить поріг 1000чоловік/день. Завдання 3. Побудова прогнозу чисельності населення України на 2100 рік. Дослідити характер зміни з часом чисельності населення України за наступними даними:
Завдання 4. Прогнозування захворюваності на грип серед населених пунктів Білоцерківського району для оптимального планування роботи швидкої медичної допомоги. Використовуючи статистичну функцію ПРЕДСКАЗ за відомими даними 5 тижнів розвитку епідемії спрогнозувати число захворілих на грип на 6-му тижні епідемії.
Вказівки до виконання завдання 1) Внести дані до електронної таблиці (рис. 58 ) 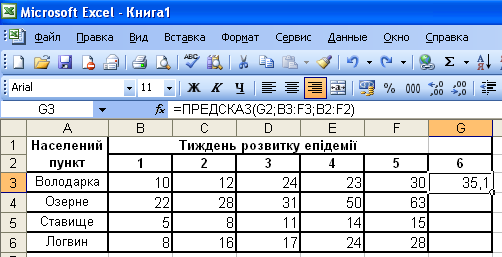 Рис. 58. Внесення даних до електронної таблиці 2) Побудуйте лінійний прогноз росту за допомогою статистичної функції ПРЕДСКАЗ. Для цього в комірку G3 вставити статистичну функцію ПРЕДСКАЗ, вказавши її аргументи:
3) Скопіюйте розрахункову формулу для комірок G4: G6. Зробіть необхідні висновки. Завдання 5. Прогнозування попиту лікарських засобів. Використовуючи статистичну функцію ПРЕДСКАЗ провести прогнозування попиту товарів аптеки на квітень наступного року.
Питання для самоконтролю1. Дайте визначення поняття «апроксимація експериментальних даних». 2. Сформулюйте задачу функціональної апроксимації. 3. Опишіть технологію підбору емпіричної формули, для якої наближення до заданої функції виявляється найкращим. 4. Обґрунтуйте необхідність прогнозування розвитку медико-біологічних процесів. 5. Опишіть комп’ютерну технологію апроксимації даних функціональними залежностями. 6. Які вбудовані функції табличного процесора MS Excel використовуються для апроксимації експериментальних даних? 7. Яке призначення лінії тренда? 8. Охарактеризуйте зміну похибки прогнозу при збільшенні кількості даних спостереження. 9. Охарактеризуйте зміну похибки прогнозу при збільшенні часового проміжку прогнозу. 10. Які типи діаграм можна побудувати в середовищі електронних таблиць MS Excel? 11. Опишіть технологію побудови діаграми. 12. Опишіть технологію редагування діаграми. 13. Як оцінити степінь наближення апроксимації експериментальних даних вибраною функцією? 14. Що показує величина достовірності апроксимації? 15. Яким чином здійснюється вибір типу апроксимуючої функції з деякого числа придатних варіантів? Завдання для самостійного виконання Завдання 1-С. .У відповідності з завданням 1 апроксимуйте дані таблиці 25 за допомогою експоненціальної функції. Визначте на основі отриманої аналітичної залежності кількість захворілих на 11, 15, 15 день від початку епідемії. Порівняйте з результатами, отриманими при виконанні завдання 1. Завдання 2-С. Виконайте завдання 1 при скороченому варіанті вхідних даних (таблиця даних розвитку епідемії містить інформацію про 7 днів розвитку епідемії). Порівняйте отримані результати з результатами розрахунків за повною таблицею 25. Завдання 3-С. Побудуйте графік росту числа захворілих на грип населених пунктів Володарки та Ставища протягом 5 тижнів за даними завдання 4. Завдання 4-С. Побудуйте графік росту числа захворілих на грип населених пунктів Володарки та Ставища протягом 5 тижнів за даними завдання 4.  Схема 3. Редагування діаграм в табличному процесорі 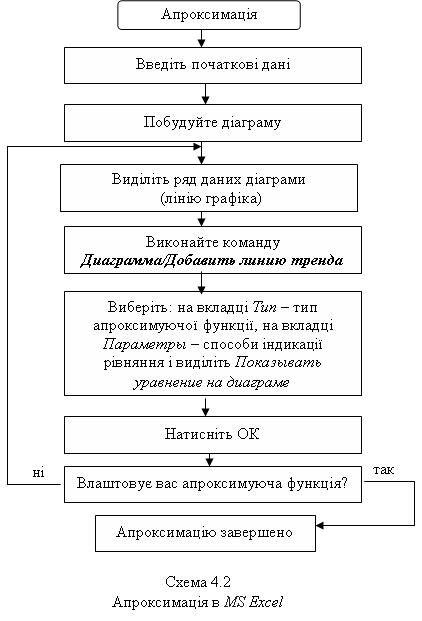 Схема 4. Апроксимація даних в середовищі табличного процесора Представлення систем підтримки прийняття рішень. Експертні системи. Побудова бази знань та структурування. Сучасна архітектура системи прийняття рішень.Конкретні цілі заняття: інтерпретувати основні моделі представлення медичних знань; аналізувати принципи побудови і функціонування систем підтримки прийняття рішень; демонструвати вміння використовувати напівактивні експертні системи для підтримки прийняття рішень. Основні поняття теми Система знань, експертна система (ЕС), база знань, штучний інтелект, система штучного інтелекту, інтелектуальні інформаційні технології, інженер зі знань, експерт, діагностика, класифікація, прогнозування, планування, керування, типи ЕС (інтерпретації даних, діагностики, моніторингу, прогнозування, навчання, планування, проектування, автономні, гібридні, формальні моделі зображення знань Короткі теоретичні відомостіПринципово нові досягнення в технології обробки інформації пов’язані зі створенням особливих людино-машинних систем, призначених для накопичення й обробки у комп’ютері знань, необхідних для вирішення складних практичних задач. Подібні системи одержали назву систем знань (knowledge based system). Серед систем знань найбільш бурхливо останнім часом розвивалися експертні системи (ЕС). У медицині ЕС широко застосовуються для підтримки прийняття рішень при розв’язанні різноманітних проблем діагностики, прогнозування, лікування, управління, навчання тощо. Продемонструємо особливості архітектури, характеристик та принципів роботи з клінічними експертними системами на прикладі програми «Експертна система» v2.0 (http://bukhnin.chat.ru/). «Експертна система» є напівактивною експертною системою, що використовує байєсовскую систему логічного висновку. Програма (див. рис. 59) призначена для проведення консультації з користувачем у деякій прикладній області (відповідно до завантаженої бази знань) з метою визначення ймовірностей можливих висновків, використовуючи для цього оцінку правдоподібності деяких передумов (свідчень), одержаних від користувача. Як приклад розглянемо задачу визначення ймовірностей наявності різних захворювань у пацієнта. Програма в цьому випадку виступає в ролі лікаря (експерта), що задає пацієнтові систему відповідних питань та на основі отриманих відомостей ставить діагноз. Причому під час діалогу користувача і програми запитується оцінка істинності ключового факту і на основі відповіді коректується ймовірність висновку та перехід до наступного актуального факту. У такий спосіб досягається швидке одержання результату при мінімальній кількості питань. Використання байєсовської системи логічного висновку означає, що оброблювана експертною системою інформація не є абсолютно точною, а носить ймовірнісний характер. Користувач не обов’язково повинен бути впевнений в абсолютній істинності або хибності відповіді, а може відповідати на запитання системи з певним ступенем впевненості. У свою чергу система видає результати консультації у вигляді ймовірностей настання висновків. 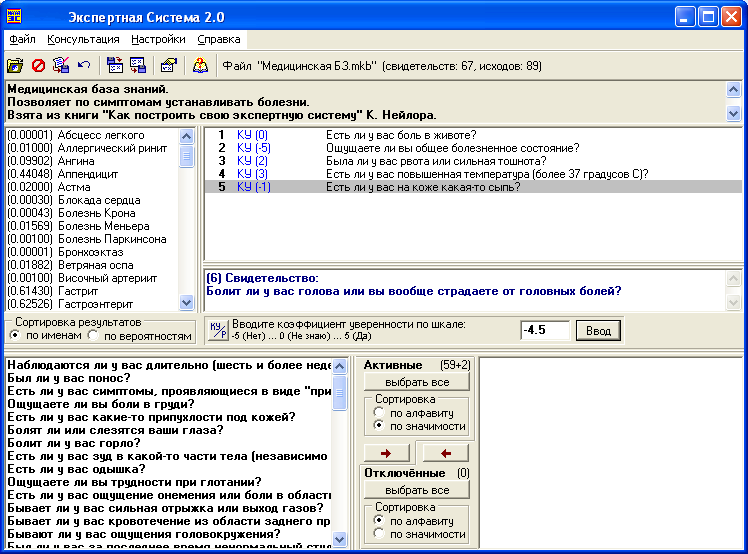 Рис. 59. Інтерфейс програми Експертна система Для початку роботи з програмою необхідно завантажити базу знань, що містить інформацію з тієї прикладної області, у якій Ви бажаєте одержати консультацію (детальний опис роботи з програмою подано в схемі 5). Після початку консультації в правій частині вікна (область запитів) з’являється перший запит системи, ступінь істинності якого система бажає дізнатися. У даній версії експертної системи можливі два способи відповіді користувача:
В обох випадках користувач має можливість вибирати будь-які проміжні значення. Ці два варіанти відповідей не тотожні, оскільки значення коефіцієнта впевненості вибирається практично інтуїтивно, в той час як імовірність може бути отримана з дослідів, математичних обрахунків тощо. Зазначимо ще одну важливу відмінність між двома способами відповіді. У випадку вибору коефіцієнта впевненості, користувач може відповісти «не знаю», ввівши число, що відповідає середині шкали (наприклад, нуль, якщо шкала від -5 до +5). Така відповідь не впливає на результат консультації. При виборі введення ймовірностей істинності відповідей такої можливості не має. Введення ймовірності істинності відповіді виправдане у випадку, коли користувач точно знає її значення. Його можна отримати з таблиць, за результатами статистичних досліджень, математичних обчислень. На схемі 6 реалізована дидактична імітаційна модель відповіді користувача на запит системи. Введена користувачем відповідь обробляється, розташовується в список, вище області запиту та підсвічується сірими кольором. При потребі користувач може виділити будь-які відповіді в цьому списку й скасувати її обробку. Одержуючи від користувача відповіді, система коректує ймовірності можливих діагнозів, що відображається в лівій частині верхньої половини вікна. По завершенні (а також у процесі) консультації передбачено можливість збереження її ходу у текстовому файлі. До протоколу буде записаний поточний час, опис бази знань, список оброблених питань та відповідей і результати консультації в тому порядку, у якому вони представлені у вікні програми. 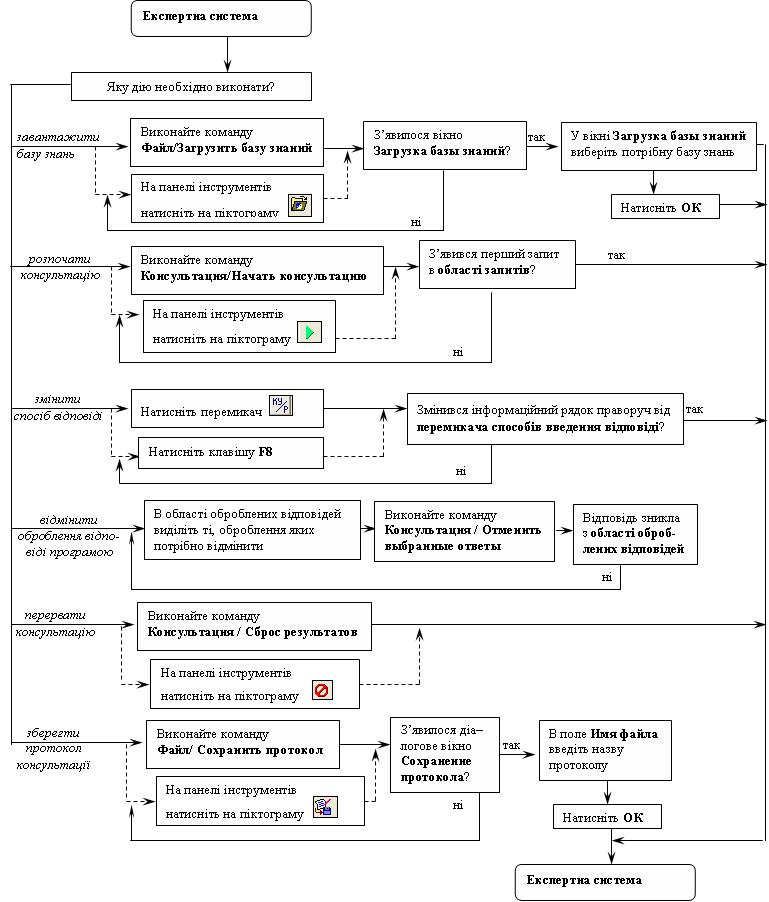 Схема 5. Модель опису роботи з програмою 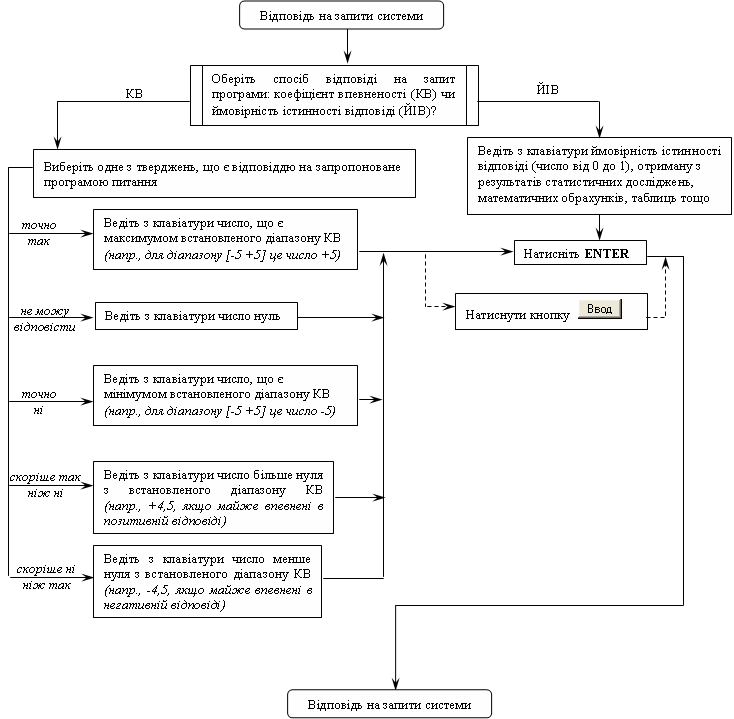 Схема 6. Модель відповіді користувача на запити системи Тестові завдання для самоконтролю1. Експертні системи що визначають зміст медичних спостережень та дослідів, називаються:
2. Експертні системи, які визначають характер відхилення стану об’єкта від норми, називаються:
3. Експертні системи, орієнтовані на нерепервну інтерпретацію даних та сигналізацію про вихід тих чи інших параметрів за допустимі межі, називається:
4. Експертні системи, які роблять ймовірнісні висновки про майбутній перебіг подій із ситуацій що склалися, називаються:
5. Експертні системи, що визначають вправи, необхідні для поліпшення підготовки майбутнього лікаря, називаються:
6. Складні програмні пакети, що акумулюють знання фахівців в конкретних галузях, і здатні давати рекомендації чи розв’язувати поставлені задачі, називаються:
7. Експертні системи, що працюють безпосередньо в режимі консультації з користувачем без застосування методів обробки даних, називаються:
8. Експертні системи, що містять стандартні пакети прикладних програм обробки, називаються:
9. Експертні системи знаходиться в активному діалозі з експертом в режимі:
10. Сукупність наукових дисциплін, що вивчають методи вирішення задач творчого характеру, з використанням електронно-обчислювальної техніки, називають:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
