Зміст модуль I. Основи інформаційних технологій в системі охорони здоровя. Обробка та аналіз медикобіологічних даних 4
 Скачать 4.71 Mb. Скачать 4.71 Mb.
|
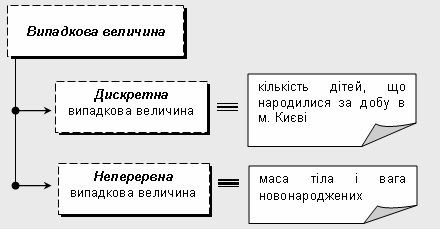
Методи біостатистикиКонкретні цілі заняття: інтерпретувати типи даних, етапи статистичного аналізу даних, види розподілів, етапи перевірки гіпотез; демонструвати вміння використовувати статистичні методи обробки медико-біологічних даних. Основні поняття теми Параметр, статистична сукупність, випадкова величина, дискретна випадкова величина, неперервна випадкова величина, генеральна сукупність, вибірка (вибіркова сукупність), варіаційний ряд, варіанта, мода, медіана, середнє арифметичне, середнє квадратичне відхилення, помилка репрезентативності, закони розподілу випадкових величин. Короткі теоретичні відомості1. Основні поняття, методи і формули біостатистики
2. Комп’ютерна технологія аналізу результатів 2.1. Оцінка вірогідності результатів прямих вимірювань Суть цього методу полягає в тому, що за знайденими значеннями Хсер і σ деякої вибірки встановлюють інтервал, у якому з певною імовірністю міститься значення деякого параметра всієї генеральної сукупності. Імовірність Р, визнана достатньою для певного висновку про досліджуваний параметр генеральної сукупності на основі вибіркових показників, називається надійною. Вибір того чи іншого значення надійної імовірності здійснюють на основі практичних міркувань і тієї відповідальності, з якою роблять висновки про параметри генеральної сукупності. У медицині при особливо відповідальних експериментах вибирають Рнад=99,9%, у решті випадків – Рнад=95%. Алгоритм оцінки вірогідності результатів прямих вимірювань. 1. Знаходження за формулою [1] середного арифметичного результатів вимірювання досліджуваної вибірки. 2. Знаходження за формулою [2] середнього квадратичного відхилення окремого результату вимірювання. 3. Знаходження за формулою [4] стандартної похибки. 4. Обчислення точності безпосереднього вимірювання Δm за формулою: Δm = mtP,ν, де tP,ν – коефіцієнт нормованих відхилень (коефіцієнт Ст’юдента), залежний від кількості степенів свободи ν=n-1, і вибраної надійної ймовірності (Рнад=99,9%, Рнад=99%, Рнад=95%). Коефіцієнт Ст’юдента знаходимо за таблицею 1.
5. Знаходження точного значення вимірюваної величини: Х = Х сер ± Δm. Цей вираз означає, що шукане значення досліджуваного параметра генеральної сукупності з вибраною надійною імовірністю не виходить за межі інтервалу: Хсер – Δm< Х <Хсер + Δm. В MS Excel для оцінки вірогідності результатів прямих вимірювань існує вбудована функція ДОВЕРИТ. 2.2. Оцінка вірогідності відмінностей дослідження двох незалежних вибірок Маємо дві групи вимірювань: дослідну х1, х2, . . . , хn та контрольну у1, у2, . . ., уn, де n1 – кількість вимірювань 1-ї групи, n2 – кількість вимірювань 2-ї групи. Використовуючи цей метод, можна встановити, чи спричинені відмінності двох незалежних вибірок випадковим фактором, чи якою-небудь зовнішньою дією (зокрема лікувальною). Алгоритм оцінки вірогідності відмінностей дослідження двох незалежних вибірок 1. Знаходження середнього арифметичного значення контрольної та дослідної груп. 2. Знаходження середнього квадратичного відхилення окремих вимірювань у групах. 3. Визначення помилок репрезентативності цих груп. 4. Знаходження абсолютного значення середніх арифметичних дослідної та контрольної груп: 5. Обчислення середньої похибки різниці. 6. Визначення критерію вірогідності різниці: 7. Знаходження кількості ступенів свободи: ν =n1+n2 - 2. 8. Знаходження за таблицею кількості ступенів свободи ν (див. нижче) значення трьох стандартних критеріїв Ст’юдента (tst), відповідних трьом програмам вірогідності (95%, 99%, 99,9%).
9. Порівняння критерію вірогідності td знайденими значеннями (tst95%, tst99%, tst99,9%). Якщо td< tst95%, то вибіркова різниця ненадійна, тобто відмінності у вибірках випадкові. Якщо tst95% ≤ td≤ tst99%, то вибіркова різниця надійна з імовірністю 95%. Якщо td≤ tst99,9%, то вибіркова різниця надійна з імовірністю 99,9%. Цей алгоритм реалізовано в Пакеті аналізу MS Excel (Сервис/Анализданных/Двухвыборочный t-тест с одинаковыми дисперсиями – для вибірок з однаковими дисперсіями, та Сервис/Анализ данных/Двухвыборочный t-тест с разными дисперсиями – для вибірок з різними дисперсіями). 2.3. Кореляційний аналіз двох випадкових ознак Цей метод застосовують для встановлення зв’язку між двома ознаками та з метою визначити його вірогідність. При цьому ми маємо виміри двох ознак: 1-а ознака – х1, х2, . . . , хn; 2-а ознака – у1, у2, . . . , уn,. Треба встановити, чи існує зв’язок між змінними ознак х і у, і якщо існує, то яка його вірогідність. Алгоритм кореляційного аналізу двох випадкових ознак 1. Знаходження середнього арифметичного значення ознак. 2. Обчислення відхилення кожного значення х від хсер: 3. Обчислення відхилення кожного значення у від усер: 4. Обчислення суми добутку відхилень: 5. Обчислення максимальної суми: 6. Знаходження коефіцієнта кореляції r: 7. Визначення глибини кореляційного зв’язку за критеріями, навединими нижче:
8. Обчислення середньої похибки коефіцієнта кореляції: 9. Обчислення критерію вірогідності коефіцієнта кореляції: 10. Визначення стандартних значень критеріїв Ст’юдента відповідно трьом програмам вірогідності (95%, 99%, 99,9%) за допомогою таблиці для кількості ступенів свободи (див. вище) ν=2n-2. 11. Порівняння коефіцієнтів вірогідності коефіцієнта кореляції стандартними значеннями критеріїв Ст’юдента. Висновок про вірогідність коефіцієнта кореляції. В MS Excel для обчислення цього параметру існує вбудована функція КОРРЕЛ. Практичні завдання Завдання 1. Обчислення основних статистичних характеристик вибірок. Визначити середнє арифметичне, середнє квадратичне відхилення, помилку репрезентативності, моду та медіану результатів вимірювання швидкості кровотоку 10 пацієнтів до наркозу.
Завдання 2. Оцінка вірогідності результатів прямих вимірювань. Оцінити вірогідність безпосередніх вимірювань швидкості кровотоку 10 пацієнтів до наркозу, використовуючи дані із завдання 1. Завдання виконати в два способи: 1) Методом безпосереднього обчислення за поданим вище алгоритмом; 2) Використовуючи вбудовані функції MS Excel. Інтерпретуйте отримані результати. Завдання 3. Оцінка вірогідності відмінностей дослідження двох незалежних вибірок. Було проведено дослідження дії магнітних полів низької частоти на карциному Герена на четвертий день захворювання (результати досліджень в таблиці:
В першому стовпчику подані результати інтактної групи, а в другому стовпчику – розмір новоутворення пухлини на яку діяли магнітні поля низької частоти. Перевірити ефективність впливу магнітних полів на новоутворення пухлини карциноми Герена. Завдання виконати двома способами: 1. Безпосередніми обчисленнями за поданим вище алгоритмом; 2. Використовуючи Пакет аналізу MS Excel. Алгоритм виконання завдання використовуючи Пакет аналізу MS Excel. 1. Обчислити дисперсії вибірок. Порівняти отримані значення дисперсій. 2. Виконати команду Сервис/Анализ данных/Двухвыборочный t-тест с разными дисперсиями. В діалоговому вікні Анализ данных вказати Интервал переменной1, тобто ввести посилання на перший діапазон даних, що аналізуються, і, містить перший стовпчик даних. Аналогічно, вказати Интервал переменной 2. Вказати Выходной диапазон, тобто ввести посилання на комірку, в яку будуть виведені результати. 3. Інтерпретація результатів аналізу. У вихідний діапазон будуть виведені: середнє, дисперсія, та число дослідів для кожної змінної, різниця середніх, df (число ступенів вільності), P(T<=t) одностороннє, t критичне одностороннє, P(T<=t) двостороннє, t критичне двостороннє. Завдання 4. Оцінка вірогідності відмінностей дослідження двох незалежних вибірок. На лабораторних щурах проводили дослідження на ембріотоксичність. Результати досліджень подані в таблиці.
В першому стовпчику подана маса плоду тварин інтактної групи, в другому – маса плоду тварин, яким в порожнину шлунку вводили 0,6% масляного розчину – токоферолу ацетату з 1 по 10 день вагітності у розрахунку 15мг/кг. Перевірити доцільність введення масляного розчину – токоферолу ацетату з 1 по 10 день вагітності (гіпотезу рівності середніх при різних об’ємах вибірки). Завдання 5. Кореляційний аналіз двох випадкових ознак Оцінка вірогідності результатів прямих вимірювань. В таблиці наведені результати спостережень частоти серцевих скорочень і частоти дихання у групі хворих з певною патологією:
Необхідно визначити, чи існує взаємозв’язок між частотою серцевих скорочень та частотою дихання при досліджуваній патології. Завдання виконати використовуючи вбудовану функцію КОРРЕЛ MS Excel. Алгоритм виконання завдання використовуючи Пакет аналізу MS Excel 1. Ввести дані до таблиці. 2. Обчислити значення коефіцієнта кореляції між вибірками. 3. В комірку вставляємо функцію КОРРЕЛ, що викликається наступним чином Мастер функций/Статистические. В поле Массив 1 вводимо дані першої вибірки, в поле Массив 2 – другої. 4. Визначити ступінь залежності між частотою дихання і частотою серцевих скорочень. Завдання 6. Кореляційний аналіз двох випадкових ознак. Визначити, чи існує взаємозв’язок між народжуваністю та смертністю (кількість на 1000 осіб) в м. Одеса, зробити висновки щодо ступеню стохастичного зв’язку. Результати досліджень подані в таблиці:
Тестові завдання для самоконтролю1. В результаті експерименту, що може бути повторений велику кількість разів, отримані значення х1, х2,..., хn, які називають:
2. Дискретною випадковою називається величина, яка приймає значення:
3. Величина, котра може приймати будь-які числові значення в даному інтервалі значень називається:
4. Функціональна залежність між значеннями випадкових величин та ймовірностями з якими вони приймають ці значення називають:
5. Властивості, що підлягають оцінці в будь-якій формі називаються:
6. Статистичною сукупністю можна назвати:
7. Якому закону розподілу підпорядковуються випадкові події такі, як число викликів швидкої допомоги за певний проміжок часу, черги до лікаря в поліклініці, епідемії?
8. Група призовників, що пройшли медичне обстеження у військкоматі протягом року є:
9. Набір значень (х1,х2,...,хn) випадкової величини Х, котрі отримані в результаті п дослідів, називається:
10. Репрезентативною називається вибіркова сукупність, яка:
11. Припущення, котрі відносяться до виду розподілу випадкової величини або окремих його параметрів є:
12. Дано вибіркову сукупність: {115; 115; 115; 120; 120; 120; 120; 120; 125}. Визначити моду.
13. Дано вибіркову сукупність: {115; 115; 115; 120; 120; 120; 120; 120; 125}. Визначити моду.
14. Ймовірність з якою може бути відхилена нульова гіпотеза, коли вона є вірною, називається:
15. При проведенні досліджень необхідно забезпечити наступні вимоги до вибірки:
16. Значення коефіцієнта кореляції може змінюватися від
17. Що характеризує абсолютне значення коефіцієнта кореляції стохастичного взаємозв’язку між випадковими величинами:
18. Знак коефіцієнта кореляції вказує
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

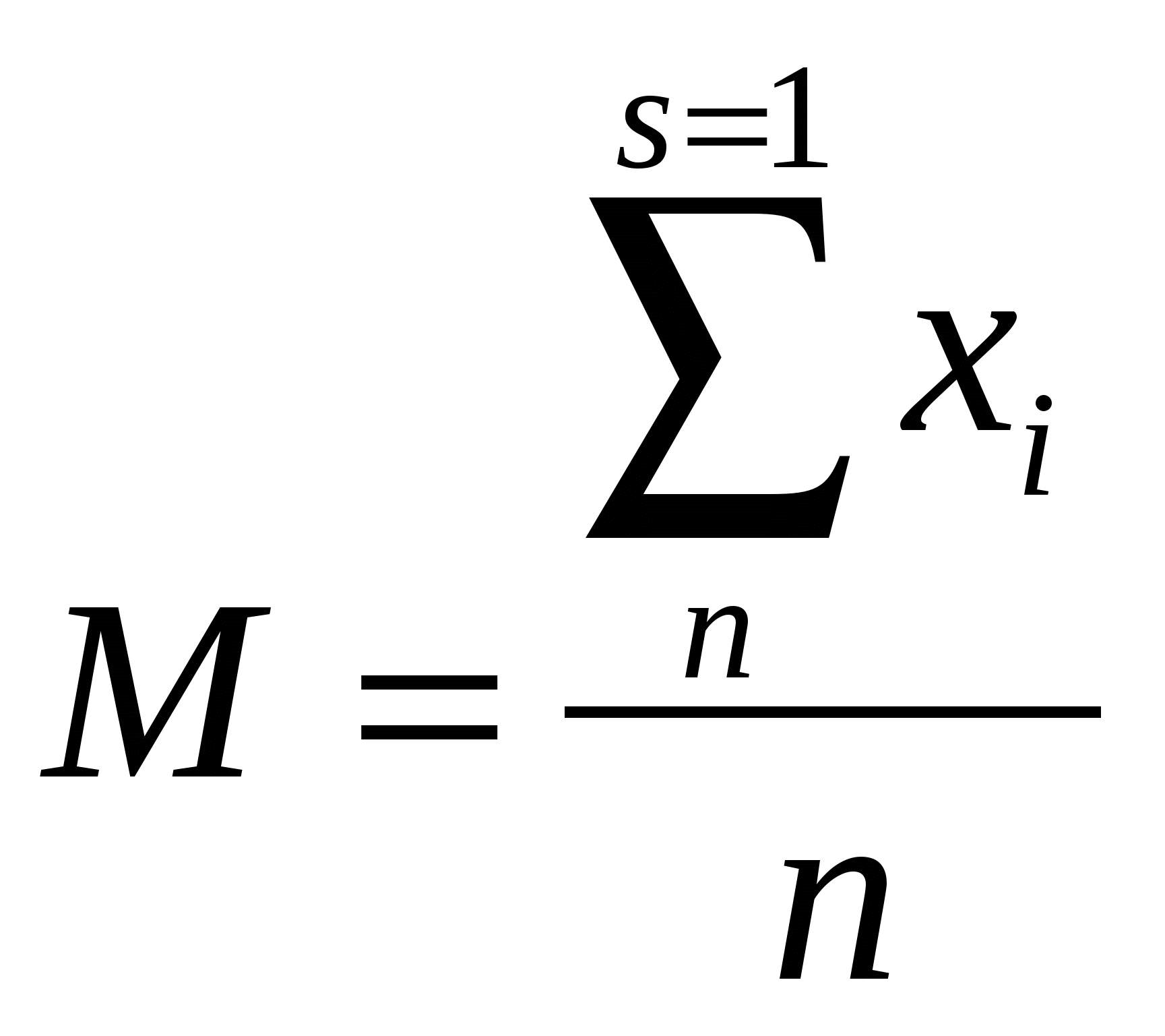 (1)
(1)
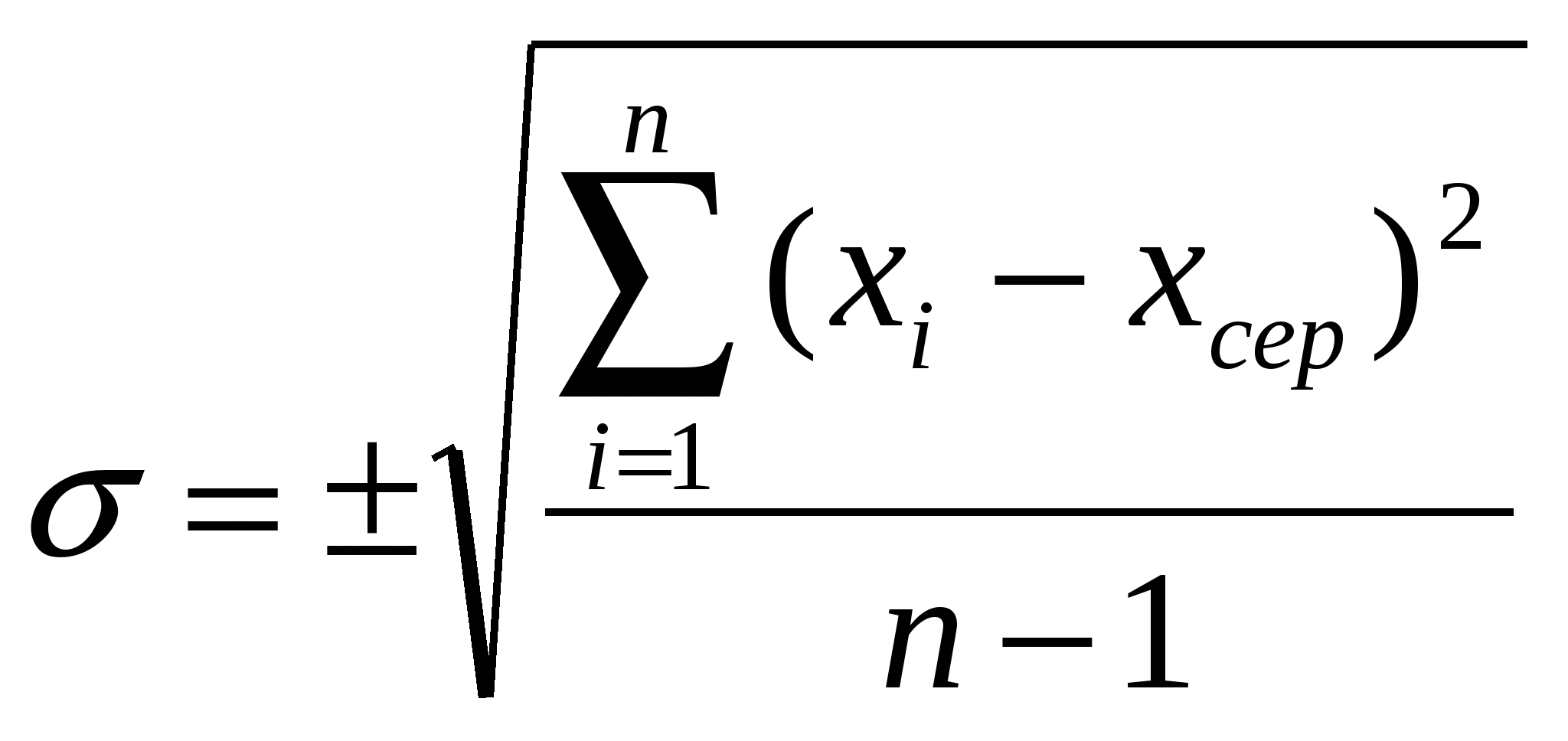 (2)
(2)