вышая матиматика. эгзамен. 13. Выражение векторного произведения через координаты. Некоторые приложения векторного произведения
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
|
13. Выражение векторного произведения через координаты. Некоторые приложения векторного произведения. Пусть заданы два вектора 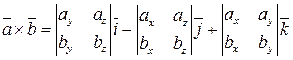 Полученную формулу можно записать еще короче: 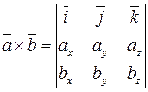 . Некоторые приложения векторного произведения Установление коллинеарности векторов Если , то (и наоборот), т.е. 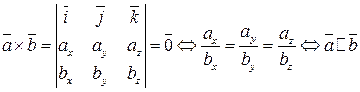 Нахождение площади параллелограмма и треугольника Согласно определению векторного произведения векторов и Определение момента силы относительно точки Пусть в точке приложена сила и пусть - некоторая точка пространства. Из физики известно, что моментом силы относительно точки называется вектор , который проходит через точку и: 1) перпендикулярен плоскости, проходящей через точки , , ; 2) численно равен произведению силы на плечо 3) образует правую тройку с векторами и . 14. Определение смешанного произведения векторов и его геометрический смысл. Смешанное произведение определяется для трех векторов, заданных в трехмерном пространстве. Смешанным произведением трех векторов 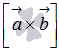 и , где и , где 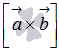 - векторное произведение векторов и . - векторное произведение векторов и .Из определения понятно, почему смешанное произведение часто называют векторно-скалярным произведением. Смешанное произведение векторов 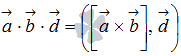 . .Геометрический смысл смешанного произведения. Выясним геометрический смысл смешанного произведения векторов Обозначим 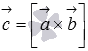 . В этом случае смешанное произведение можно записать как . В этом случае смешанное произведение можно записать как 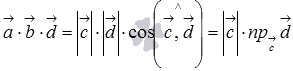 , где , где 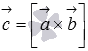 . .Абсолютная величина числовой проекции 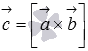 перпендикулярен и вектору и вектору по определению векторного произведения. А в разделе геометрический смысл векторного произведения мы выяснили, что величина перпендикулярен и вектору и вектору по определению векторного произведения. А в разделе геометрический смысл векторного произведения мы выяснили, что величина 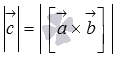 представляет собой площадь параллелограмма, построенного на векторах и . Таким образом, модуль смешанного произведения представляет собой площадь параллелограмма, построенного на векторах и . Таким образом, модуль смешанного произведения 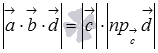 - это произведение площади основания на высоту параллелепипеда, построенного на векторах - это произведение площади основания на высоту параллелепипеда, построенного на векторах |
