математика. РАЗДЕЛ 2 Случайные величины doc. Определение Величина, которая в зависимости от случая может принимать те или другие числовые значения, называется случайной
 Скачать 1.49 Mb.
|
|
РАЗДЕЛ 2 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Выше рассматривались события, состоящие в появлении того или иного числа в результате проведения некоторого вероятностного эксперимента. Например, при бросании игральной кости могли появиться числа 1, 2, 3, 4, 5 и 6. Наперед определить число выпавших очков невозможно, поскольку оно зависит от многих случайных причин, которые полностью не могут быть учтены. В этом смысле появление числа очков на игральной кости есть величина случайная, т.е. числа 1, 2, 3, 4, 5 и 6 есть возможные значения этой величины. Определение 1. Величина, которая в зависимости от случая может принимать те или другие числовые значения, называется случайной. Надо отметить то, что случайные величины (сокращенно СВ) есть математические модели вероятностных экспериментов. Примерами случайных величин являются: количество деталей высокого качества, сошедших с конвейера в течение смены; количество зерен в случайно взятом колосе; результат измерения длины, массы, времени и т.д. Уже из рассмотренных примеров можно заключить о целесообразности различать случайные величины, принимающие лишь отдельные, изолированные значения и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток. Поэтому рассматривают дискретные и непрерывные случайные величины (обозначаются кратко СВ). Определение 2. Дискретной (прерывной) (обозначаются ДСВ) называется случайная величина, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений ДСВ может быть конечным или бесконечным. Определение 3. Непрерывной (обозначается НСВ) называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений НСВ – бесконечно. Замечание: Настоящее определение НСВ не является точным. Более строгое определение будет дано позднее. В дальнейшем случайные величины будем обозначать заглавными буквами латинского алфавита X, Y, Z и т.д. Значения, которые эти величины могут принимать, обозначаются малыми буквами x, y, z, a, b, , и т.д. 1. ДИСКРЕТНЫЕ ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 1.1. Закон распределения ДСВ. Функция распределения ДСВ Значения ДСВ можно записать в виде конечной или бесконечной последовательности  . Для каждого из этих значений  определяют соответствующую вероятность  .Определение 1.1. Законом распределения ДСВ называют соответствие между возможными значениями СВ и их вероятностями  .Закон распределения ДСВ можно задать таблично, аналитически (в виде формулы) и графически. Если закон распределения ДСВ задают таблично, иначе называют рядом распределения, то таблица принимает следующий вид: Таблица 1.1
Для ряда распределения должны выполняться два требования: 1)  (вероятности не могут быть отрицательными величинами);2)  .Если X принимает конечное число значений, то такая ДСВ называется конечнозначной. В целях наглядности закон распределения ДСВ можно изобразить и графически, для чего в прямоугольной системе координат строят точки  , а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.Закон распределения ДСВ задается еще функцией распределения. Определение 1.2. Для ДСВ X с законом распределения функция распределения имеет вид , (1.1)где суммирование распространяется на все те индексы  , для которых  .Графиком функции распределения для ДСВ является кусочно-постоянная функция. Свойства функции распределения функция распределения монотонно не убывает; функция распределения непрерывна слева;  .Пример 1.1. Вероятности безотказной работы двух технических устройств за время  соответственно равны  и  . Построить ряд распределения СВ X, где СВ X число безотказно работающих технических устройств за время . Построить функцию распределения.Решение. СВ X в задачи могут принимать следующие значения:  ни одно техническое устройство не работало безотказно за время ;  только одно техническое устройство работало безотказно за время ;  оба технических устройства работало безотказно за время .Так как и , то  и  .Найдем вероятности появления каждой из СВ X:  ; ; .Тогда получаем следующий ряд распределения:  .Проверка:  .Найдем функцию распределения ДСВ X. Значения СВ X:  разбивают числовую прямую на четыре промежутка  .Если  , то  .Если  , то  .Если  , то  .Если  , то  .Таким образом, получаем следующую функцию распределения: 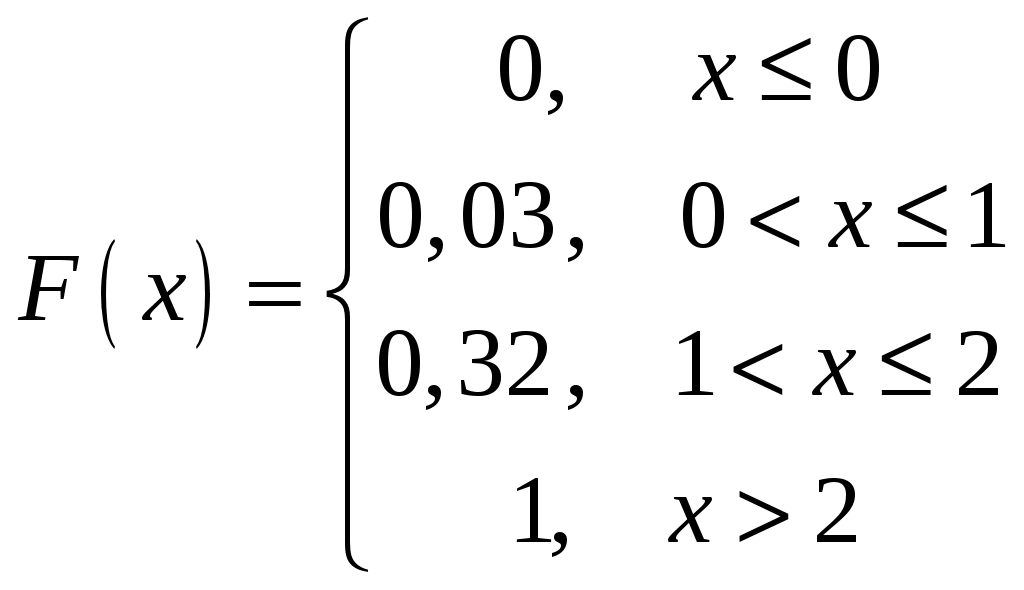 . 1.2. Числовые характеристики ДСВ Можно считать, что закон распределения полностью характеризует СВ. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают СВ суммарно: такие числа называют числовыми характеристиками СВ. К числу важных числовых характеристик относятся: математическое ожидание, дисперсия, среднее квадратическое отклонение, мода, медиана. Определение 1.3. Математическим ожиданием ДСВ (обозначается  )называют сумму произведения всех ее возможных значений  на их вероятности  : . (1.2)Замечание: Из определения следует, что математическое ожидание ДСВ есть неслучайная (постоянная) величина. В случае счетнозначной величины, которая может принимать значения x1, x2, …, xn, … с вероятностями p1, p2, …, pn, …,  ,где предполагается абсолютная сходимость ряда, в противном случае считают, что у данной СВ нет математического ожидания. Математическое ожидание приближенно равно среднему значению СВ. Прежде чем рассмотреть свойства математического ожидания, введем еще несколько понятий: независимые СВ, произведение независимых СВ, сумма СВ. Определение 1.4. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Несколько случайных величин называют взаимно независимыми, если законы распределения любого числа из них не зависит от того, какие возможные значения приняли остальные величины. Определение 1.5. Произведением независимых случайных величин  и  называют случайную величину  , возможные значения которой равны произведениям каждого возможного значения на каждое возможное значение . Вероятности возможных значений произведения равны произведениям вероятностей возможных значений сомножителей.Определение 1.6. Суммой случайных величин и называют случайную величину  , возможные значения которой равны суммам каждого возможного значения с каждым возможным значением . Вероятности возможных значений для независимых величин и равны произведениям вероятностей слагаемых; для зависимых – произведениям вероятности одного слагаемого на условную вероятность второго.Пример 1.2. Даны законы распределения двух независимых ДСВ. Найти закон распределения . и 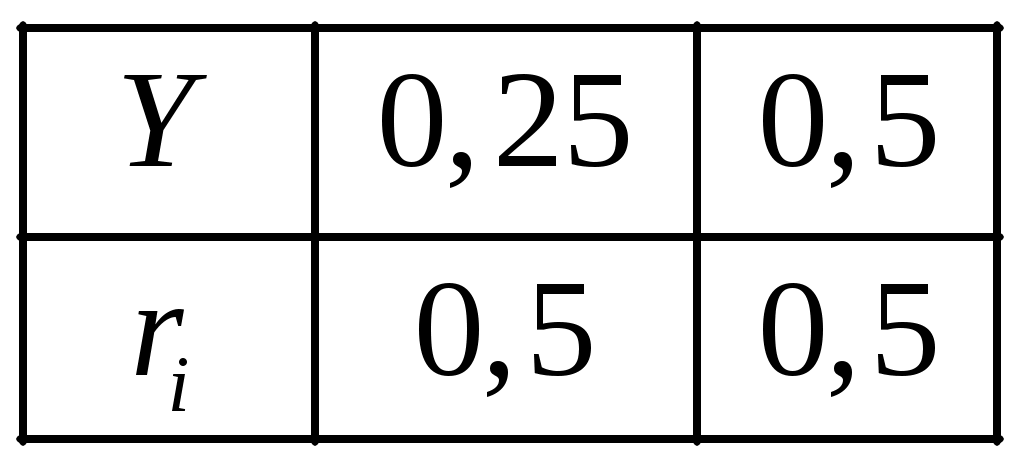 .Решение. 1) Составим закон распределения СВ  . Случайные величины и их вероятности принимают следующие значения: и  ; , и  ; и  .Тогда закон распределения имеет вид: 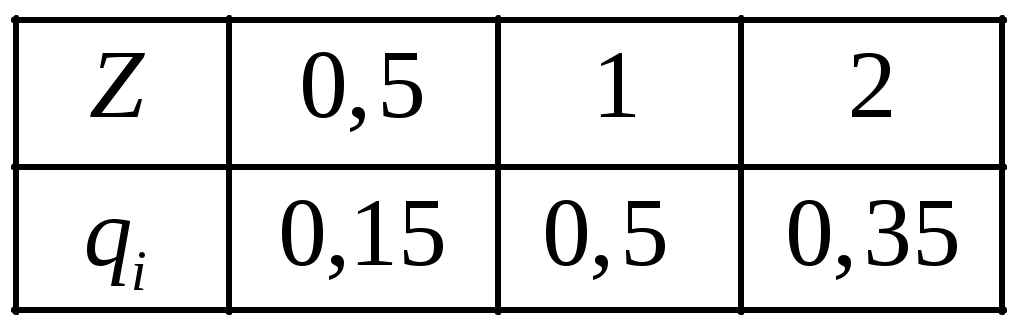 . Свойства математического ожидания Свойство 1. Математическое ожидание постоянной величины  равно самой постоянной: .Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: .Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:  .Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:  .Свойства примем без доказательства. Как мы отметили выше, математическое ожидание СВ характеризует среднее этой СВ, это центр ее распределения. Вторая отличительная особенность СВ – степень разброса этой величины по отношению к ее центру. Наиболее употребительной оценкой указанного разброса является дисперсия. На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения СВ и затем найти их средне значение. Однако такой путь ничего не даст, так как среднее значение отклонения, т.е.  для любой СВ. Это объясняется тем, что одни возможные отклонения положительны, а другие – отрицательны; в результате их взаимное погашение среднее значение отклонения равно нулю. |
