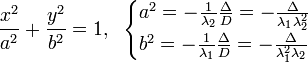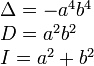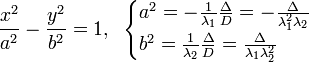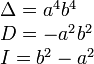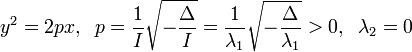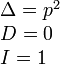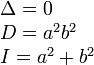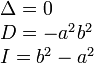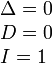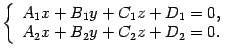Математика. Определители. Свойства. Вычисление. Определитель или детерминант

Название	Определители. Свойства. Вычисление. Определитель или детерминант
Анкор	Математика.docx
Дата	24.02.2018
Размер	0.67 Mb.
Формат файла
Имя файла	Математика.docx
Тип	Документы #15865
страница	1 из 7

1 2 3 4 5 6 7

Определители. Свойства. Вычисление.
Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.
Определитель матрицы А обозначается как: det(A), |А| или Δ(A).
Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам): $\delta (\hat a_1, \ldots, \alpha\hat a_i+\beta\hat {a\'}_i, \ldots, \hat a_n) = \alpha\delta (\hat a_1, \ldots, \hat a_i, \ldots, \hat a_n)+ \beta\delta (\hat a_1, \ldots, \hat {a\'}_i, \ldots, \hat a_n)$ , где и т. д. — строчки матрицы, $\delta (\hat a_1, \ldots, \hat a_i, \ldots, \hat a_n)$ — определитель такой матрицы.

При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.

-Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.

-Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.

-Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

-Общий множитель элементов какого-либо ряда определителя можно вынести зазнак определителя.

-Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.

-Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.

-Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

-Определитель произведения квадратных матриц одинакового порядка равепроизведению их определителей (cм. также формулу Бине-Коши).

-С использованием индексной нотации определитель матрицы 3×3 может быть определён с помощью символа Леви-Чивита из соотношения: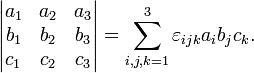

$\begin{vmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \\ \end{vmatrix} =\sum_{i,j,k=1}^3 \varepsilon_{ijk} a_{i} b_{j} c_{k}.$

Решение систем линейных уравнений методом Крамера

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.

Для системы n линейных уравнений с n неизвестными (над произвольным полем)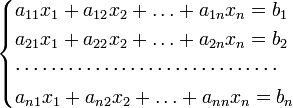

$\begin{cases} a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n = b_1\\ a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n = b_2\\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots\cdots\\ a_{n1}x_1 + a_{n2}x_2 + \ldots + a_{nn}x_n = b_n\\ \end{cases}$

с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде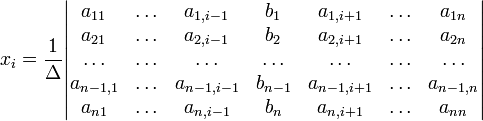

$x_i=\frac{1}{\delta}\begin{vmatrix} a_{11} & \ldots & a_{1,i-1} & b_1 & a_{1,i+1} & \ldots & a_{1n} \\ a_{21} & \ldots & a_{2,i-1} & b_2 & a_{2,i+1} & \ldots & a_{2n} \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ a_{n-1,1} & \ldots & a_{n-1,i-1} & b_{n-1} & a_{n-1,i+1} & \ldots & a_{n-1,n} \\ a_{n1} & \ldots & a_{n,i-1} & b_n & a_{n,i+1} & \ldots & a_{nn} \\ \end{vmatrix}$

(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство: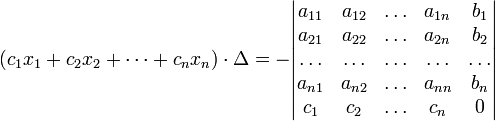

$(c_1x_1+c_2x_2+\dots+c_nx_n)\cdot\delta = -\begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n} & b_1\\ a_{21} & a_{22} & \ldots & a_{2n} & b_2\\ \ldots & \ldots & \ldots & \ldots & \ldots\\ a_{n1} & a_{n2} & \ldots & a_{nn} & b_n\\ c_{1} & c_{2} & \ldots & c_{n} & 0\\ \end{vmatrix}$

В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b₁,b₂,...,b_n и x₁,x₂,...,x_n, либо набор c₁,c₂,...,c_n состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

Система линейных уравнений: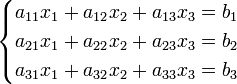

$\begin{cases} a_{11}x_1 + a_{12}x_2 + a_{13}x_3 = b_1\\ a_{21}x_1 + a_{22}x_2 + a_{23}x_3 = b_2\\ a_{31}x_1 + a_{32}x_2 + a_{33}x_3 = b_3\\ \end{cases}$

Определители:

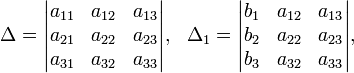$\delta=\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{vmatrix},\ \ \delta_1=\begin{vmatrix} b_1 & a_{12} & a_{13} \\ b_2 & a_{22} & a_{23} \\ b_3 & a_{32} & a_{33} \\ \end{vmatrix},\ \$

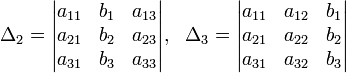$\delta_2=\begin{vmatrix} a_{11} & b_1 & a_{13} \\ a_{21} & b_2 & a_{23} \\ a_{31} & b_3 & a_{33} \\ \end{vmatrix},\ \ \delta_3=\begin{vmatrix} a_{11} & a_{12} & b_1 \\ a_{21} & a_{22} & b_2 \\ a_{31} & a_{32} & b_3 \\ \end{vmatrix}$

Решение:

$x_1=\frac{\delta_1}{\delta},\ \ x_2=\frac{\delta_2}{\delta},\ \ x_3=\frac{\delta_3}{\delta}$

Пример:

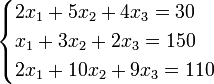$\begin{cases} 2x_1 + 5x_2 + 4x_3 = 30\\ x_1 + 3x_2 + 2x_3 = 150\\ 2x_1 + 10x_2 + 9x_3 = 110\\ \end{cases}$

Определители:

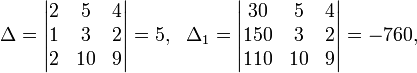$\delta=\begin{vmatrix} 2 & 5 & 4 \\ 1 & 3 & 2 \\ 2 & 10 & 9 \\ \end{vmatrix}=5,\ \ \delta_1=\begin{vmatrix}30&5&4\\150&3&2\\ 110 & 10 & 9 \\ \end{vmatrix}=-760,\ \$

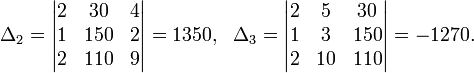$\delta_2=\begin{vmatrix} 2 & 30 & 4 \\ 1 & 150 & 2 \\ 2 & 110 & 9 \\ \end{vmatrix}=1350,\ \ \delta_3=\begin{vmatrix} 2 & 5 & 30 \\ 1 & 3 & 150 \\ 2 & 10 & 110 \\ \end{vmatrix}=-1270.$

$x_1=-\frac{760}{5}=-152,\ \ x_2=\frac{1350}{5}=270,\ \ x_3=-\frac{1270}{5}=-254$

Метод Крамера требует вычисления n + 1 определителей размерности . При использовании метода Гаусса для вычисления определителей, метод имеет временную сложность порядка O(n⁴), что хуже, чем если бы метод Гаусса напрямую использовался для решения системы уравнений. Поэтому метод считался непрактичным. Однако в 2010 году было показано, что метод Крамера может быть реализован со сложностью O(n³), сравнимой со сложностью метода Гаусса.^[1]

Решение систем линейных уравнений методом Гаусса.
Ме́тод Га́усса^[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные
Пусть исходная система выглядит следующим образом

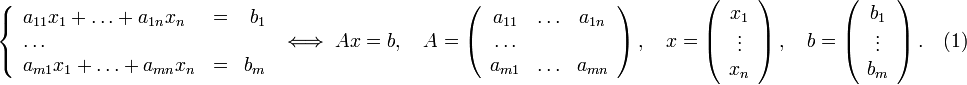$\left\{\begin{array}{lcr} a_{11}x_1+\ldots+a_{1n}x_n &=& b_1 \\ \ldots & & \\ a_{m1}x_1+\ldots+a_{mn}x_n &=& b_m \\ \end{array}\right.\iff ax = b,\quad a=\left( \begin{array}{ccc} a_{11} & \ldots & a_{1n}\\ \ldots & & \\ a_{m1} & \ldots & a_{mn} \end{array}\right),\quad x = \left( \begin{array}{c}x_1 \\ \vdots \\ x_n \end{array} \right), \quad b = \left( \begin{array}{c}b_1 \\ \vdots \\ b_m \end{array} \right).\quad (1)$

Матрица A называется основной матрицей системы, b — столбцом свободных членов.

Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):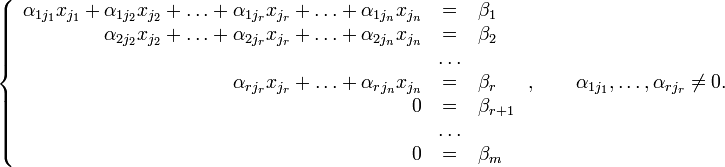

$\left\{\begin{array}{rcl} \alpha_{1j_1}x_{j_1}+\alpha_{1j_2}x_{j_2}+\ldots+\alpha_{1j_r}x_{j_r}+\ldots+\alpha_{1j_n}x_{j_n} &=& \beta_1 \\ \alpha_{2j_2}x_{j_2}+\ldots+\alpha_{2j_r}x_{j_r}+\ldots+\alpha_{2j_n}x_{j_n} &=& \beta_2 \\ &\ldots& \\ \alpha_{rj_r}x_{j_r}+\ldots+\alpha_{rj_n}x_{j_n} &=& \beta_r \\ 0 &=& \beta_{r+1} \\ &\ldots& \\ 0 &=& \beta_m \end{array}\right.,\qquad \alpha_{1j_1},\ldots,\alpha_{rj_r}\neq 0.$

При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных ^[3].

Тогда переменные называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число , где i > r, то рассматриваемая система несовместна.

Пусть для любых i > r.

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом ( 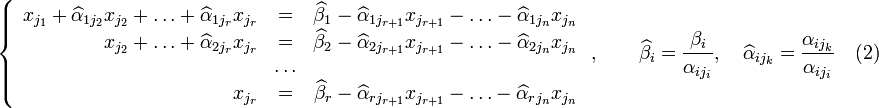$\alpha_{ij_i},\, i=1,\ldots,r\!$ , где — номер строки):

$\left\{\begin{array}{rcc} x_{j_1}+\widehat{\alpha}_{1j_2}x_{j_2}+\ldots+\widehat{\alpha}_{1j_r}x_{j_r}&=& \widehat{\beta}_1-\widehat{\alpha}_{1j_{r+1}}x_{j_{r+1}}-\ldots- \widehat{\alpha}_{1j_n}x_{j_n} \\ x_{j_2}+\ldots+\widehat{\alpha}_{2j_r}x_{j_r}&=& \widehat{\beta}_2-\widehat{\alpha}_{2j_{r+1}}x_{j_{r+1}}-\ldots- \widehat{\alpha}_{2j_n}x_{j_n} \\ &\ldots& \\ x_{j_r}&=& \widehat{\beta}_r-\widehat{\alpha}_{rj_{r+1}}x_{j_{r+1}}-\ldots- \widehat{\alpha}_{rj_n}x_{j_n} \\ \end{array}\right., \qquad \widehat{\beta}_i=\frac{\beta_i}{\alpha_{ij_i}},\quad \widehat{\alpha}_{ij_k}=\frac{\alpha_{ij_k}}{\alpha_{ij_i}}\quad (2)$ ,
где $i=1,\ldots,r,\quad k=i+1,\ldots,n.\!$

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.

На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.

На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

Метод Гаусса требует порядка O(n³) действий.

Достоинства метода:  Менее трудоёмкий по сравнению с другими методами.

 Позволяет однозначно установить, совместна система или нет, и если совместна, найти её решение.

 Позволяет найти максимальное число линейно независимых уравнений — ранг матрицы системы

Матрицы. Действия над матрицами. Свойства матриц.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.

Матрицы допускают следующие алгебраические операции:

сложение матриц, имеющих один и тот же размер;

умножение матриц подходящего размера (матрицу, имеющую n столбцов, можно умножить справа на матрицу, имеющую n строк);

умножение матрицы на элемент основного кольца или поля (т. е. скаляр).

Особое значение в теории матриц занимают всевозможные нормальные формы, то есть канонический вид, к которому можно привести матрицу заменой координат.
Прямоугольной матрицей размера m´n называется совокупность mn чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде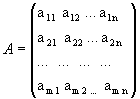



Числа a_{i j}, составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы A = (a_{i j}) и B = (b_{i j}) одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если a_{i j} = b_{i j}.Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера m´n, все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами.

Обратная Матрица.

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

$\! aa^{-1} = a^{-1}a = e$

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Свойства обратной матрицы:

$\det a^{-1} = \frac{1}{\det a}$ , где обозначает определитель.

$\ (ab)^{-1} = b^{-1}a^{-1}$ для любых двух обратимых матриц A и B.

$\ (a^t)^{-1} = (a^{-1})^t$ где * ^T обозначает транспонированную матрицу.

$\ (ka)^{-1} = k^{-1}a^{-1}$ для любого коэффициента .

Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A ^{− 1} существует, то x = A ^{− 1}b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

Решение систем линейных уравнений матричным методом.

Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с n неизвестными (над произвольным полем):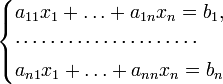

${ \begin{cases} a_{11}x_1+ \ldots +a_{1n}x_n=b_1, \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ a_{n1}x_1+ \ldots +a_{nn}x_n=b_n \end{cases} }$

Тогда её можно переписать в матричной форме:

AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно: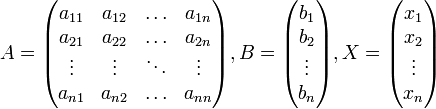

$a = \begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{pmatrix}, b = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix}, x = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}$

Умножим это матричное уравнение слева на A ^{− 1} — матрицу, обратную к матрице A: $a^{-1}\left( ax \right) = a^{-1}b$

Так как A ^{− 1}A = E, получаем X = A ^{− 1}B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:

$\det a \ne 0$ .

Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть ненулевое) решение только если det A = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

[править] Пример решения неоднородной СЛАУ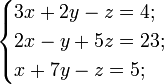

${ \begin{cases} 3x+2y-z=4; \\ 2x-y+5z=23;\\ x+7y-z=5; \end{cases} }$

Сначала убедимся в том, что определитель матрицы из коэффициентов при неизвестных СЛАУ не равен нулю.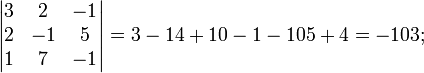

$\begin{vmatrix} 3 & 2 & -1 \\ 2 & -1 & 5 \\ 1 & 7 & -1 \end{vmatrix}=3-14+10-1-105+4=-103;$

Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы.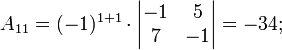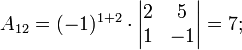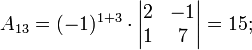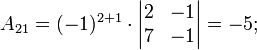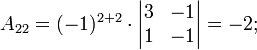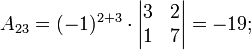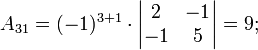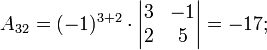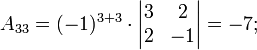

$a_{11}=(-1)^{1+1}\cdot \begin{vmatrix}-1 & 5\\ 7 & -1 \end{vmatrix}=-34;$

$a_{12}=(-1)^{1+2}\cdot \begin{vmatrix}2 & 5\\ 1 & -1 \end{vmatrix}=7;$

$a_{13}=(-1)^{1+3}\cdot \begin{vmatrix}2 & -1\\ 1 & 7 \end{vmatrix}=15;$

$a_{21}=(-1)^{2+1}\cdot \begin{vmatrix}2 & -1\\ 7 & -1 \end{vmatrix}=-5;$

$a_{22}=(-1)^{2+2}\cdot \begin{vmatrix}3 & -1\\ 1 & -1 \end{vmatrix}=-2;$

$a_{23}=(-1)^{2+3}\cdot \begin{vmatrix}3 & 2\\ 1 & 7 \end{vmatrix}=-19;$

$a_{31}=(-1)^{3+1}\cdot \begin{vmatrix}2 & -1\\ -1 & 5 \end{vmatrix}=9;$

$a_{32}=(-1)^{3+2}\cdot \begin{vmatrix}3 & -1\\ 2 & 5 \end{vmatrix}=-17;$

$a_{33}=(-1)^{3+3}\cdot \begin{vmatrix}3 & 2\\ 2 & -1 \end{vmatrix}=-7;$

Далее найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы.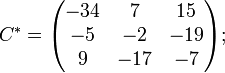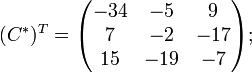

$c^{}=\begin{pmatrix}-34 & 7 & 15\\ -5 & -2 & -19\\ 9 & -17 & -7\end{pmatrix};$

$(c^{})^{t}=\begin{pmatrix}-34 & -5 & 9\\ 7 & -2 & -17\\ 15 & -19 & -7\end{pmatrix};$

$a^{-1}=\frac{1}{\det a}\cdot(c^{})^{t}$

Подставляя переменные в формулу, получаем: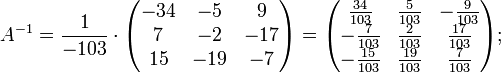

$a^{-1}=\frac{1}{-103}\cdot\begin{pmatrix}-34 & -5 & 9\\ 7 & -2 & -17\\ 15 & -19 & -7\end{pmatrix}= \begin{pmatrix}\frac{34}{103} & \frac{5}{103} & -\frac{9}{103}\\ -\frac{7}{103} & \frac{2}{103} & \frac{17}{103}\\ -\frac{15}{103} & \frac{19}{103} & \frac{7}{103}\end{pmatrix};$

Осталось найти неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.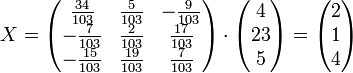

$x=\begin{pmatrix}\frac{34}{103} & \frac{5}{103} & -\frac{9}{103}\\ -\frac{7}{103} & \frac{2}{103} & \frac{17}{103}\\ -\frac{15}{103} & \frac{19}{103} & \frac{7}{103}\end{pmatrix}\cdot \begin{pmatrix}4\\23\\5\end{pmatrix}=\begin{pmatrix}2\\1\\4\end{pmatrix}$

Итак, x=2; y=1; z=4.

Векторы. Линейные операции над векторами.

Скалярное произведение двух векторов.
Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины* данного вектора x на проекцию другого вектора y на данный вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Обычно используется одно из следующих обозначений:

,

,

,

или (обозначение Дирака, часто применяемое в квантовой механике для векторов состояния):

.

Обычно предполагается что скалярное произведение положительно определено, то есть

$\langle \mathbf a, \mathbf a \rangle> 0$ для всех .

Векторное произведение двух векторов.

Векторным произведением вектора на вектор в пространстве называется вектор , удовлетворяющий следующим требованиям:

длина вектора равна произведению длин векторов и на синус угла ; между ними

$\left| \mathbf c \right| = \left| \mathbf a \right| \left| \mathbf b \right| \sin \varphi$

вектор ортогонален каждому из векторов и

вектор направлен так, что тройка векторов является правой.

в случае пространства требуется ассоциативность тройки векторов .

Обозначение:

$\mathbf c = \left[ \mathbf a \mathbf b \right] = \left[ \mathbf a,\; \mathbf b \right] = \mathbf a \times \mathbf b$

В литературе^[1] определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.

Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводиться остальное.

Смешанное произведение трёх векторов.

Тройкой векторов называются три вектора, если указано, какой из них считается первым, какой вторым и какой третьим. Тройку векторов записывают в порядке нумерации; например, запись , , означает, что вектор считается первым, - вторым, - третьим.

Тройка некомпланарных векторов , , называется правой, если составляющие ее векторы, будучи приведены к общему началу, располагаются в порядке нумерации аналогично тому, как расположены большой, указательный и средний пальцы правой руки. Если векторы , , расположены аналогично тому, как расположены большой, указательный и средний пальцы левой руки, то тройка этих векторов называется левой.

Смешанным произведенем трех векторов , , называется число, равное векторному произведению , умноженному скалярно на вектор , то есть .

Имеет место тождество, ввиду чего для обозначения смешанного произведения употребляется более простой символ . Таким образом,

, .

Смешанное произведение равно объему параллелепипеда, построенного на векторах , , , взятого со знаком плюс, если тройка правая, и со знаком минус, если эта тройка левая. Если векторы , , компланарны (и только в этом случае), смешанное произведение равно нулю; иначе говоря, равенство

есть необходимое и достаточное условие компланарности векторов , , .

Если векторы , , заданы своими координатами:

, , ,

то смешанное произведение определяется формулой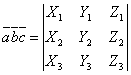

.

Напомним, что система координатных осей предполагется правой (вместе с тем является правой и тройка векторов , , ).

11. Прикладные задачи векторного анализа: Объем параллелепипеда

объем параллелепипеда

     Если параллелепипед построен на приведенных к общему началу векторах , а , , , - радиус-векторы его соответствующих вершин то объем параллелепипеда

     В координатах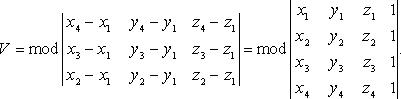

12. Прикладные задачи векторного анализа: Площадь тетраэдра.
13. Прикладные задачи векторного анализа: Площадь треугольника

14. Прикладные задачи векторного анализа: Площадь параллелограмма
По определению векторного произведения двух векторов модуль векторного произведения равен площади параллелограмма, построенного на этих векторах. Поэтому для решения задачи найдем сначала векторное произведение , а пото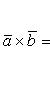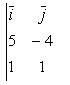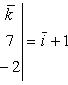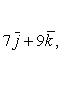м его модуль. Согласно

имеем

а модуль

Искомая площадь параллелограмма

S = 19,26 кв. ед.

Замечание.

Векторное произведение можно было сразу определить по формуле

в которой следует взять

a_x = 5; a_y = -4; a_z = 7;

b_x = 1; b_y = 1; b_z = -2.

15. Прямая на плоскости. Угол между двумя прямыми.
Прямая — одно из основных понятий геометрии.

При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.

Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.

Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то сможете найти угол. Точнее, косинус угла по формуле:

16. Уравнение прямой.
Общее уравнение прямой линии на плоскости в декартовых координатах:

$ax+by+c=0,\,$

где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде :

17. Кривые второго порядка.

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

$</h2>a_{11}x^2 + a_{22}y^2+2a_{12}xy+2a_{13}x+2a_{23}y+a_{33}=0,$

в котором по крайней мере один из коэффициентов отличен от нуля.

Вводом новой системы координат можно привести уравнения кривых второго порядка к стандартному каноническому виду (см. таблицу). Параметры канонических уравнений весьма просто выражаются через инварианты и корни характеристического уравнения (см. выше раздел «Характеристическая квадратичная форма и характеристическое уравнение»).

Вид кривой

Каноническое уравнение

Инварианты

Невырожденные кривые ()

Эллипс

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,\;\; \begin{cases} a^2 = - \frac{1}{\lambda_2}\frac{\delta}{d} = -\frac{\delta}{\lambda_1\lambda^2_2} \\ b^2 = - \frac{1}{\lambda_1}\frac{\delta}{d} = -\frac{\delta}{\lambda^2_1\lambda_2} \end{cases}$

$\begin{array}{l} \delta = -a^4b^4 \\ d = a^2b^2 \\ i = a^2+b^2 \end{array}$

Гипербола

$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1,\;\; \begin{cases} a^2 = - \frac{1}{\lambda_1}\frac{\delta}{d} = -\frac{\delta}{\lambda^2_1\lambda_2} \\ b^2 = \frac{1}{\lambda_2}\frac{\delta}{d} = \frac{\delta}{\lambda_1\lambda^2_2} \end{cases}$

$\begin{array}{l} \delta = a^4b^4 \\ d = -a^2b^2 \\ i = b^2 - a^2 \end{array}$

Парабола

$y^2=2px,\;\; p=\frac{1}{i}\sqrt{-\frac{\delta}{i}} = \frac{1}{\lambda_1}\sqrt{-\frac{\delta}{\lambda_1}}> 0,\;\; \lambda_2=0$

$\begin{array}{l} \delta = p^2 \\ d = 0 \\ i = 1 \end{array}$

Вырожденные кривые (Δ = 0)

Точка

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=0$

$\begin{array}{l} \delta = 0 \\ d = a^2b^2 \\ i = a^2+b^2 \end{array}$

Две пересекающиеся прямые

$\frac{x^2}{a^2}-\frac{y^2}{b^2}=0$

$\begin{array}{l} \delta = 0 \\ d = -a^2b^2 \\ i = b^2 - a^2 \end{array}$

Две параллельные прямые

$\begin{array}{l} \delta = 0 \\ d = 0 \\ i = 1 \end{array}$

Одна прямая

x² = 0

$\begin{array}{l} \delta = 0 \\ d = 0 \\ i = 1 \end{array}$

Для центральной кривой в каноническом виде её центр находится в начале координат.

18. Общее уравнение кривых второго порядка.

Общее уравнение кривой можно записать в матричном виде

$\begin{pmatrix} x & y & 1 \end{pmatrix} \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{12} & a_{22} & a_{23} \\ a_{13} & a_{23} & a_{33} \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = 0.$

19. Плоскость. Уравнение плоскости.

Пло́скость — одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.

Общее уравнение (полное) плоскости

$ax+by+cz+d=0\qquad (1)$

где и — постоянные, причём и одновременно не равны нулю; в векторной форме:

$(\mathbf{r},\mathbf{n})+d=0$

где — радиус-вектор точки , вектор $\mathbf{n}=(a,b,c)$ перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора :

$\cos \alpha = \frac{a}{\sqrt{a^2+b^2+c^2}},$

$\cos \beta = \frac{b}{\sqrt{a^2+b^2+c^2}},$

$\cos \gamma = \frac{c}{\sqrt{a^2+b^2+c^2}}.$

Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При плоскость проходит через начало координат, при (или , ) П. параллельна оси (соответственно или ). При (, или ) плоскость параллельна плоскости (соответственно или ).

Уравнение плоскости в отрезках:

$\frac{x}{a}+ \frac{y}{b}+ \frac{z}{c}=1,$

где , , — отрезки, отсекаемые плоскостью на осях и .

Уравнение плоскости, проходящей через точку перпендикулярно вектору нормали $\mathbf{n}(a,b,c)$ :

в векторной форме:

$((\mathbf{r}-\mathbf{r_0}),\mathbf{n})=0.$

Уравнение плоскости, проходящей через три заданные точки , не лежащие на одной прямой:

$((\mathbf{r}-\mathbf{r_1}),(\mathbf{r_2}-\mathbf{r_1}),(\mathbf{r_3}-\mathbf{r_1}))=0$

(смешанное произведение векторов), иначе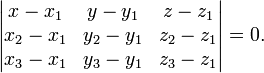

$\left| \begin{matrix}x-x_1&y-y_1&z-z_1\\ x_2-x_1&y_2-y_1&z_2-z_1\\ x_3-x_1&y_3-y_1&z_3-z_1\\ \end{matrix}\right|=0.$

Нормальное (нормированное) уравнение плоскости

$x \cos \alpha+ y \cos \beta+ z \cos \gamma - p=0 \qquad (2)$

в векторной форме:

$(\mathbf{r},\mathbf{n^0})\mathbf{-p}=0,$

где - единичный вектор, — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель

$\mu = \pm \frac{1}{\sqrt{a^2+b^2+c^2}}$

(знаки и противоположны).

20. Взаимное расположение двух плоскостей. Угол между двумя плоскостями.
Взаимное расположение двух плоскостей

     Если , то они:

     1) пересекаются

     2) параллельны (но не совпадают)

     3) совпадают

     Если плоскости заданы уравнениями и 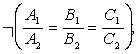то случаи 1 - 3 имеют месло, когда:

     1)

     2)

     3)

     Угол между плоскостями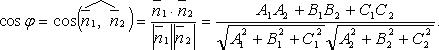

21. Прямая в пространстве. Уравнение прямой в пространстве.

Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.

Итак, если уравнения двух непараллельных плоскостей -- ${a_1x+b_1y+c_1z+d_1=0}$ и ${a_2x+b_2y+c_2z+d_2=0}$ , то прямая, являющаяся их линией пересечения, задается системой уравнений

$\displaystyle \left\{\begin{array}{l} a_1x+b_1y+c_1z+d_1=0,\\ a_2x+b_2y+c_2z+d_2=0.\end{array}\right.$

(11.11)

И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.
22. Взаимное расположение прямой и плоскости.

Прямая и плоскость в пространстве могут:

а) не иметь общих точек;

б) иметь ровно одну общую точку;

в) иметь хотя бы две общие точки.

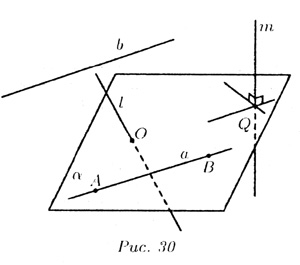На рис. 30 изображены все эти возможности.

В случае а) прямая b параллельна плоскости: b || .

В случае б) прямая l пересекает плоскость в одной точке О; l = О.

В случае в) прямая а принадлежит плоскости : а или а .

Теорема. Если прямая b параллельна хотя бы одной прямой а, принадлежащей плоскости , то прямая параллельна плоскости .

Предположим, что прямая m пересекает плоскость в точке Q.Если m перпендикулярна каждой прямой плоскости , проходящей через точку Q, то прямая m называется перпендикулярной к плоскости .

Трамвайные рельсы иллюстрируют принадлежность прямых плоскости земли. Линии электропередачи параллельны плоскости земли, а стволы деревьев могут служить примерами прямых, пересекающих поверхность земли, некоторые перпендикулярные плоскости земли, другие — не перпендикулярные (наклонные).
1 2 3 4 5 6 7