Основы химической термодинамики
 Скачать 2.79 Mb. Скачать 2.79 Mb.
|
 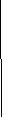    ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ
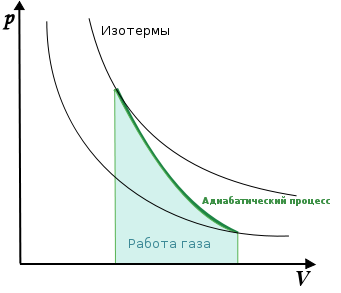 График адиабаты (жирная линия) на диаграмме для газа. —давлениегаза; — объём. В частном случае, когда работа совершается через изменение объёма, можно определить её следующим способом: пусть газ заключён в цилиндрический сосуд, плотно закрытый легко скользящим поршнем, если газ будет расширяться, то он будет перемещать поршень и при перемещении на отрезок совершать работу[9][10] где F — сила, с которой газ действует на поршень. Перепишем уравнение: где s — площадь поршня. Тогда работа будет равна[9][10] где — давление газа, — малое приращение объёма. Аналогично видно, что уравнение выполняется и для сосудов с произвольной поперечной формой сечения
При нагревании жидких и твердых тел их объем практически не изменяется, и работа расширения оказывается равной нулю. Поэтому все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов: CV – молярная теплоемкость в изохорном процессе (V = const) и Cp – молярная теплоемкость в изобарном процессе(p = const). В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует
Изменение ΔU внутренней энергии газа прямо пропорционально изменению ΔT его температуры. Для процесса при постоянном давлении первый закон термодинамики дает:
где ΔV – изменение объема 1 моля идеального газа при изменении его температуры на ΔT. Отсюда следует:
Отношение ΔV / ΔT может быть найдено из уравнения состояния идеального газа, записанного для 1 моля:
где R – универсальная газовая постоянная. При p = const
Таким образом, соотношение, выражающее связь между молярными теплоемкостями Cp и CV, имеет вид (формула Майера):
6. Внутренняя энергия и энтальпия си, их взаимосвязь. Зависимость внутренней энергии и энтальпии вещества от температуры. Интегрирование соответствующих уравнений. Внутренней энергией системы называется сумма потенциальной энергии взаимодействия всех частиц тела между собой и кинетической энергией их движения, т.е. внутренняя энергия системы складывается из энергии поступательного и вращательного движения молекул, энергии внутримолекулярного колебательного движения атомов и атомных групп, составляющих молекулы, энергии вращения электронов в атомах, энергии, заключающейся в ядрах атомов, энергии межмолекулярного взаимодействия и других видов энергии. Абсолютная величина внутренней энергии тела неизвестна, но для изучения химических явления важно знать только изменение внутренней энергии при переходе системы из одного состояния в другое.Во многих процессах передача энергии может осуществляться частично в виде теплоты и частично в виде работы. Таким образом, теплота и работа характеризуют качественно и количественно две различные формы передачи энергии от одного тела к другому; они измеряются в тех же единицах, что и энергия. Работу или энергию любого видаможно представить как произведение двух факторов: фактора интенсивности на изменение фактора емкости, называемого также фактором экстенсивности (если фактор интенсивности остается постоянным во время процесса).Так, например, обычная работа (механическая), равна произведению приложенной силы на приращение пути: При изохорном процессе А=0, т.к. изменения объема системы не происходит ( V=0).Следовательно, переходу системы, предположим из состояния 1 в состояние 2 отвечает равенство: Для изобарического процесса V - разность между суммой объемов продуктов реакций и суммой объемов исходных веществ (Р=const). или Обозначим, Энтальпияравна сумме внутренней энергии и произведения объема на давление. Энтальпия как и внутренняя энергия является экстенсивной функцикй состояния, зависящей от природы вещества, давления и температуры. В пределах температурной области где фазовое состояние системы не меняется, энтальпия является монотонной функцией основных параметров. Энтальпия является функцией состояния, т.е. её изменение определяется заданными начальными и конечными состояниями системы и не зависит от пути перехода. dim [H]=[кДж] или [кДж/моль] Таким образом, при изохорическом процессе тепловой эффект реакции: внутренняя энергия идеального газа не зависит от объема и давления, а является лишь функцией температуры, то на основании уравнения (2.7) после его интегрирования получим для внутренней энергии при любой температуре T: UТ = Uо + сV (Т – Тo). (5.2) Энтальпия идеального газа, как и внутренняя энергия, также зависит только от температуры. Так как, по определению, H = U + pV, а для 1 моля газа pV = RT и (ср – сV) =R, то Н = Uо + ср (Т – Тo). (5.3) Изохорный и изобарный потенциалы идеального газа при постоянной температуре определяются интегрированием уравнений (4.28) и (4.34). Для одного моля идеального газа при T = const dF = – pdV = – F = F(Т) – RTlnV. (5.5)
Закон Гесса — основной закон термохимии, который формулируется следующим образом:
Иными словами, количество теплоты, выделяющееся или поглощающееся при каком-либо процессе, всегда одно и то же, независимо от того, протекает ли данное химическое превращение в одну или в несколько стадий (при условии, что температура, давление и агрегатные состояния веществ одинаковы). 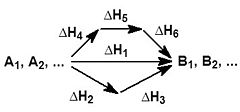 На рисунке приведено схематическое изображение некоторого обобщенного химического процесса превращения исходных веществ А1, А2… в продукты реакции В1, В2…, который может быть осуществлен различными путями в одну, две или три стадии, каждая из которых сопровождается тепловым эффектом ΔHi. Согласно закону Гесса, тепловые эффекты всех этих реакций связаны следующим соотношением: | |||||||||||||||||||||||||||||||||||||||