Роль статистики в бизнесе. Лекция+1+ВВЕДЕНИЕ+РОЛЬ+СТАТИСТИКИ+В+БИЗНЕСЕ. Тема 1 введение роль статистики в бизнесе 1 Статистические методы в управлении Статистика
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
|
ТЕМА 1 ВВЕДЕНИЕ: РОЛЬ СТАТИСТИКИ В БИЗНЕСЕ 1.1 Статистические методы в управлении Статистика – это искусство и наука сбора и анализа данных. Поскольку данными называют любой вид зарегистрированной информации, статистика играет важную роль во всех сферах деятельности человека. Данные очень часто используются в менеджменте. Приведем краткий перечень видов ежедневно используемой информации: Финансовые отчеты (и др. виды бух. отчетности) Курсы валют, банковские процентные ставки Состояние бюджета Отчеты о продажах Результаты обзора состояния рынка Данные о качестве продукции Отчеты о производительности рабочих и т.д. Что должен знать о статистике менеджер?: иметь представление об основных понятиях статистики; принимать непосредственное участие в статистическом исследовании, если он отвечает за сбор или анализ данных; понимать и использовать результаты статистического анализа. Целесообразно выделить три вида научной и прикладной деятельности в области статистических методов управления: а) разработка и исследование методов общего назначения, без учета специфики области применения; б) разработка и исследование статистических моделей реальных явлений и процессов в соответствии с потребностями той или иной области деятельности; в) применение статистических методов и моделей для статистического анализа конкретных данных. Люди, занимающиеся бизнесом, вынуждены принимать решения в условиях постоянного давления обстоятельств, зачастую не имея полной и точной информации. Конечно же, любую доступную информацию следует использовать максимально полно. Статистический анализ помогает извлекать информацию из данных и оценивать качество этой информации. Вероятность помогает понять риски и случайности и обеспечивает оценки правдоподобности получения различных потенциальных результатов. Основные этапы статистического анализа: Планирование исследования – включает составление подробного плана сбора данных, возможно с использованием случайной выборки их генеральной совокупности. Случайная выборка является одним из наилучших способов извлечь для подробного изучения выборку из генеральной совокупности, которая слишком велика, чтобы ее можно было изучить полностью. Планирование сбора данных в маркетинговых исследованиях называют планированием выборочного исследования, а в изучении оптимизации химического производственного процесса – планированием эксперимента. Предварительное исследование данных включает рассмотрение набора данных с разных точек зрения, описание и обобщение данных. Выполнение этого этапа помогает убедиться, что запланированный анализ адекватен данным, а при необходимости позволяет внести в процесс анализа определенные коррективы. Оценивание неизвестной величины дает наиболее обоснованное возможное предположение о значении, основанное на исходных данных. Кроме того, есть возможность вычислить величину ошибки, которая возникает при использовании оценки вместо фактического, но неизвестного значения. Примеры неизвестных величин для оценивания: - объем продаж в следующем квартале; - намерения правительства по изменению налоговых ставок; - уровень брака в производственном процессе; - изменение производительности при изменении стратегии и т.д. ПОМНИТЕ, ЧТО ВСЕ СТАТИСТИЧЕСКИЕ ОЦЕНКИ ЯВЛЯЮТСЯ ТОЛЬКО ПРЕДПОЛОЖЕНИЯМИ, А, СЛЕДОВАТЕЛЬНО, ЧАСТО БЫВАЮТ НЕТОЧНЫ Статистическая оценка также показывает величину неопределенности или ошибки в некотором предположении, рассчитанном для выборки, случайно взятой из большей по размеру генеральной совокупности Проверка статистических гипотез заключается в использовании данных для выбора одной из двух (или больше) различных возможностей при решении вопроса при неопределенной ситуации. Такая проверка позволяет убедиться, действительно ли данные обладают определенным интересным свойством или имеем дело с «чистой случайностью», которая не представляет интереса. Примеры гипотез, которые можно было бы проверить с использованием данных: - новое медицинское средство безопасно и эффективно; - средство марки «Х» эффективно стирает и отбеливает; - исходя из прошлого опыта можно предсказать ситуацию на фондовом рынке; - уровень производственного брака ниже, чем ожидают потребители продукции. Каждая гипотеза сформулирована как определенное утверждение, которое может быть либо верным, либо неверным. Результатом проверки гипотезы является заключение о том, что данные либо подтверждают гипотезу, либо нет. ПРИМЕР На стадии планирования следует решить, что и как часто следует измерять. Например, можно принять решение извлекать случайную выборку объемом 5 изделий из каждой партии объемом 500 изделий. Каждое изделие в выборке оценивают по внешнему виду, выявляя очевидный брак, а также измеряя длину и ширину изделия. Результат стадии планирования исследования представляет собой план раннего выявления проблем. План должен работать в реальном времени, чтобы проблемы можно было выявлять немедленно, а не на следующей неделе. В ходе предварительного исследования данные наносят на контрольные карты и изучают отклонения. Правильно определив направление изменения данных, можно предсказать и установить проблему раньше, чем она приведёт к производственным потерям. Статистическая оценка обеспечивает менеджмент информацией о ходе производственного процесса. Если производственный процесс хорошо управляется в установленных границах, то можно даже поднять сортность продукции, а значит и цену. Статистическую проверку гипотез можно использовать для ответа на важный вопрос: контролируется ли данный процесс или нет? Расскажите о 4 этапах статистического анализа на примере запуска нового продукта. Статистические методы управления следует рассматривать как важную часть процесса принятия управленческих решений, позволяющую вырабатывать обоснованные стратегические решения, сочетающие интуицию специалиста с тщательным анализом имеющейся информации. 1.2 Количественные методы в управлении Количественные методы исследований нацелены на получение количественной информации о большом числе объектов исследования: покупателей, потребителей, предприятий. Главной задачей количественных исследований является получение численной оценки изучаемой темы. Такие исследования применяются, когда необходимы точные, статистически надежные количественные данные. В основе количественных методов исследований всегда лежат строгие статистические модели, используются большие выборки. Это позволяет не просто получить мнения и предположения, а выяснить точные количественные значения изучаемых показателей. То есть результаты количественных исследований статистически достоверны, их можно экстраполировать на всю изучаемую совокупность. Исследования с использованием количественных методов – это основной инструмент получения необходимой информации для планирования и принятия решений в случае, когда необходимые гипотезы относительно поведения потребителей уже сформированы при помощи качественных методов. Количественные методы можно охарактеризовать как «формализованные» или «массовые». Под формализацией понимается степень направленности методики на строгую фиксацию определенного набора переменных и их количественное измерение. Так, мы можем с помощью опроса выяснить предпочтения потребителей по поводу того, или иного продукта и выразить это в процентах. Характерной особенностью количественных методов является то, что исследуемые переменные заданы исследователем заранее, и отступление от них в процессе сбора данных невозможно. Залог успеха любого исследования – его системность и комплексный подход к решению поставленных задач. Методы в управлении подразделяются на: 1. Количественные исследования. Количественные исследования так называются по причине нацеленности на получение количественной информации о большом количестве объектов исследования (потребителей, предприятий). Главной задачей количественных исследований является получение численной оценки состояния рынка или реакции респондентов на некое событие. Такие исследования применяются, когда необходимы точные, статистически надежные численные данные. Основные методы количественных исследований – это различные виды опросов. Опрос – это метод сбора первичной информации, предусматривающий, во-первых, устное или письменное обращение исследователей к определённой группе людей с вопросами, содержание которых отражает изучаемую проблему; во-вторых, регистрацию и статистическую обработку полученных ответов, а так же их теоретическую интерпретацию. Количественный опрос позволит: сегментировать рынок, узнать о предпочтениях потребителей, установить уровень осведомлённости и лояльности потребителей к торговой марке, просчитать доли рынка, составить рейтинг участников рынка и т.д. Существуют количественные исследования следующих видов: – квартирный опрос – опрос населения по месту жительства; – уличный опрос – опрос населения в общественных местах; – телефонный опрос – опрос посредством телефонного разговора интервьюера с респондентом; – экспертный опрос – опрос специалистов определённых профессий или лиц, занимающих определенную должность; – холл-тест – респонденты тестируют определенный товар и/или его элементы (упаковку, рекламный ролик и т. п.), а затем отвечают на вопросы (заполняют анкету), касающиеся данного товара; – хоум-тест – респонденты исследуют какой-либо продукт (товар) или несколько продуктов (товаров) в реальной домашней обстановке; – аудит розничных точек (Retail-audit) – анализ ассортимента, цен, дистрибьюции, мерчандайзинговых материалов в розничных точках по исследуемой товарной группе; – таинственный покупатель (Mystery Shopping) – это использование специально подготовленных покупателей для анонимной оценки качества обслуживания потребителей, работы персонала, его честности, проверки выполнения стандартов мерчандайзинга, качества продуктов и услуг. Mystery Shopping существует под различными названиями: – секретный покупатель; – таинственный покупатель; – анонимный аудит; – виртуальный покупатель; – оценка сотрудников; –телефонная проверка. 2. Качественные исследования. Качественные методы предполагают сбор информации в свободной форме; они фокусируются не на статистических измерениях, а опираются на понимание, объяснение и интерпретацию эмпирических данных, являются источником формирования гипотез и продуктивных идей. Задача методов качественных исследований – получить разведочные данные, а не количественное распределение мнений. В качественных методах для того, чтобы объяснить, интерпретировать понятия, используются не цифры, а слова. Полученные качественными методами данные не подлежат количественному анализу. Проще говоря, они отвечают не на вопрос «сколько», а на вопросы «что», «как» и «почему». Основные направления использования количественных методов в управлении: 1. Социально-экономические исследования и моделирование экономики региона и города. Деятельность по данному направлению направлена на решение следующих задач: – проведение анализа динамики показателей социально-экономического развития; – оценивание функций доходов работников при официальной и незарегистрированной занятости; – построение моделей отдачи от образования с точки зрения доходов с учетом сигналов на рынке труда; – применение геоинформационных технологий в экономике. 2. Исследование структуры промышленного производства в регионах Казахстана и межрегиональной торговли. Деятельность по данному направлению направлена на решение следующих задач: – анализ новых направлений теоретических исследований в области экономики агломерации; – проведение статистических и эконометрических исследований, включающих изучение общих тенденций изменения пространственной структуры промышленности Казахстана в отраслевом и региональном разрезе, выявление основных факторов и механизмов этого процесса; – анализ сравнительных преимуществ различных регионов и выделение конкурентоспособных отраслей. 3. Исследование и применение количественных методов анализа в финансовой сфере. Деятельность по данному направлению направлена на решение следующих задач: – разработка методов оптимального оценивания и прогнозирования нестационарных временных рядов со скачкообразными изменениями параметров и шоковыми возмущениями в случайные моменты времени; – проведение статистического анализа полученных алгоритмов с помощью математического моделирования; – применение разработанных методов для исследования реальных процессов и наблюдаемых временных рядов в финансах и экономике; – определение состава и значения показателей оценки состоятельности казахстанских организаций. ТЕМА 2 СТРУКТУРЫ ДАННЫХ 2.1 Классификация различных типов наборов данных Данные могут быть представлены в различной форме. Набор данных состоит из результатов наблюдений объектов, обычно включающих регистрацию одной и той же информации для каждого объект, называемых элементарными единицами. В качестве объектов могут выступать компании, люди, города или что угодно, что представляет интерес для изучения. Для каждого из объектов регистрируют один и тот же признак (или признаки). Признак, который регистрируют для каждого из объектов, называется переменной. Результатами измерений или наблюдений – объемы продаж, вес, доход, население, размер, стоимость. Существует три основных способа классификации набора данных: По количеству переменных (одномерный, двумерный и многомерный). По типу представленной каждой из переменных информации (числа или категории). Зависимости от того, является ли набор данных временным рядом, или это данные об одном временном срезе. Одномерные наборы данных содержат только один признак, зарегистрированный для каждой элементарной единицы. Например, доходы отдельных людей, выявленные в ходе маркетингового исследования; количество дефектов в каждом телевизоре из выборки объемом 50, взятой из телевизоров, изготовленных сегодня утром; оценки платежеспособности фирм в инвестиционном портфеле. Наборы двумерных данных содержат информацию о двух признаках для каждого из объектов. В дополнение к обобщению свойств каждой из этих двух переменных, рассматриваемых как отдельные наборы одномерных данных, статистические методы можно использовать для изучения связи между этими двумя измеренными факторами. Например, данные о размерах прибыли компаний и изменения прибыли; данные за прошлый квартал о затратах на производство продукции и количестве произведенных изделий; данные опроса 100 человек в торговом центре: приобреталось или не приобреталось некоторое изделие (первая переменная записывает ответ да/нет), и возможность вспомнить рекламу этого изделия (вторая переменная) Наборы многомерных данных содержат информацию о трех или более признаках для каждого объекта. В дополнение к обобщению свойств каждой из этих переменных и установлению зависимости между парами переменных статистические методы можно использовать для изучения взаимосвязей между этими переменными. Например, темп роста и набор характеристик стратегии, таких как тип оборудования, объем инвестиций, стиль руководства; заработная плата, а также пол, стаж работы, производительность для каждого служащего. Значения переменных, которые регистрируются как числа, имеющие содержательный смысл называют количественными данными. Дискретная количественная переменная может принимать значения только из некоторого списка конкретных чисел. Например, сколько раз за последние 24 часа на предприятии выключали компьютер; количество действительно заключенных контрактов из 18 подготовленных вами предложений. Любую количественную переменную, которая не является дискретной называют непрерывной. Если переменная содержит информацию о том, какой из нескольких нечисловых категорий принадлежит объект, то она называется качественной переменной. Существует два типа качественных данных: порядковые (имеющие содержательный смысл, порядок). Например, должность, записанная для каждого из группы руководителей: президент, вице-президент, начальник отдела, зам. начальника отдела; ответы на вопрос анкеты «Пожалуйста выскажите свое мнение относительно вашей работы в фирме, используя шкалу от 1 до 5». номинальные (нет содержательно-интерпретируемого порядка). Например, главный продукт каждого их нескольких производственных предприятий диверсифицированного бизнеса, как, например пластмасса, электроника, древесина; название всех фирм, указанных на первой странице выпуска. Если последовательность записи данных имеет содержательный смысл, то соответствующий набор данных представляет собой временной ряд. Например, цена за пшеницу за последние 50 лет с учетом инфляции; объемы месячных продаж за последние 20 лет. Если последовательность записи данных не важна, то соответствующий набор содержит данные об одном временном срезе. Например, количество телефонных звонков вчера, измеренная для 30 человек продолжительность сна в последнюю ночь. 2.2 Описание данных: графики и таблицы Таблицы частот и гистограммы. Таблицы частот или одновходовые таблицы представляют собой простейший метод анализа категориальных переменных. Часто их используют как одну из процедур разведочного анализа, чтобы просмотреть, каким образом различные группы данных распределены в выборке. Например, изучая зрительский интерес к разным видам спорта (с целью рекламы какого-либо продукта на ТВ), вы могли бы представить ответы респондентов следующей таблицей:
Таблица показывает частоты, кумулятивные (накопленные) частоты, процент, кумулятивный процент респондентов, выразивших свой интерес к просмотру футбольных матчей в следующей шкале: (1)Всегда интересуюсь, (2) Обычно интересуюсь, (3) Иногда интересуюсь или (4) Никогда не интересуюсь. Таблица частот показывает, сколько объектов попадает в ту или иную категорию. Практически каждый исследовательский проект начинается с построения таблиц частот. Например, в социологических опросах таблицы частот могут отображать число респондентов из определенной этнических групп, голосовавших за того или иного кандидата и т.д. Ответы, измеренные в определенной шкале (например, в шкале: интерес к футболу) также можно прекрасно свести в таблицу частот. В медицинских исследованиях табулируют пациентов с определенными симптомами. В маркетинговых исследованиях – покупательский спрос на товары разного типа у разных категорий населения. В промышленности – частоту выхода из строя элементов устройства, приведших к авариям или отказам всего устройства при испытаниях на прочность (например, для определения того, какие детали телевизора действительно надежны после эксплуатации в аварийном режиме при большой температуре, а какие нет). Обычно, если в данных имеются группирующие переменные, то для них всегда вычисляются таблицы частот.
Гистограмма – ступенчатая фигура, состоящая из 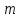 прямоугольников, опирающихся на частичные интервалы. Высота каждого столбца, соответствующего каждой категории, пропорциональна количеству точек в данной категории. Гистограмма частот также является статистическим аналогом кривой плотности распределения. прямоугольников, опирающихся на частичные интервалы. Высота каждого столбца, соответствующего каждой категории, пропорциональна количеству точек в данной категории. Гистограмма частот также является статистическим аналогом кривой плотности распределения.Чем выше высота столбца, тем больше точек попало в соответствующий диапазон. Поскольку диапазоны имеют равные длины, то можно сказать и так: чем выше столбец, тем больше плотность точек в соответствующем диапазоне. Формы гистограмм. Далее рассмотрим несколько примеров, в которых гистограммы принимают различные формы. В каждом из этих примеров наиболее важным является не техническое воспроизведение данной гистограммы, а ее содержательная интерпретация. Симметричные гистограммы. Гистограммы данного типа имеют один пик и примерно одинаковое расположение столбцов слева и справа от пика. Чаще всего это столбцы уменьшающейся высоты по мере их удаления от центра.  Гистограммы со скосом направо (положительный скос). Гистограммы данного типа имеют пик, и значения рассматриваемой переменной распространяются вправо от пика намного дальше, чем влево.  Гистограммы со скосом влево (отрицательный скос). Гистограммы данного типа имеют пик, и значения рассматриваемой переменной распространяются влево от пика намного дальше, чем вправо.  Гистограммы с несколькими пиками. Гистограммы данного типа часто возникают, когда данные объединяют в себе выборки из различных генеральных совокупностей. Например, это могут быть данные, относящиеся к мужчинам и женщинам, или результаты опросов, проведенных в разных регионах. Гистограммы, содержащие два пика, называют бимодульными.  Анализ взаимозависимостей с помощью диаграмм рассеивания (разброса). Часто интерес представляет вопрос о наличии взаимосвязи между двумя величинами. В этом случае целесообразно их значения интерпретировать как координаты, что позволяет изобразить некоторую совокупность точек на координатной плоскости. Эта совокупность и называется диаграммой рассеивания. Диаграмма разброса – инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных. Анализируя расположение точек совокупности, можно сделать вывод о наличии (или отсутствии) взаимосвязи между величинами, а также о силе и характере этой зависимости. Кроме того, представление данных двух выборок в виде диаграммы рассеивания может выявить некоторые взаимосвязи (или их отсутствие) в отдельных подмножествах данных выборок. Для выявления связи между ними и служит диаграмма разброса, которую также называют полем корреляции.    n=25  В зависимости от расположения точек в поле рассеивания можно предварительно проанализировать характер зависимости между переменными. Если точки выстраиваются на условной наклонной линии снизу вверх, то имеется положительная зависимость (корреляция), если точки выстраиваются по линии сверху вниз – отрицательная корреляция. Если на глаз невозможно определить корреляцию, то зависимость между двумя переменными, скорее всего, отсутствует. Возможно наличие на графике точек, стоящих в стороне от основного массива данных. Это может быть вызвано как ошибками измерения или описками в записи, так и случайными выбросами, которые можно не учитывать в анализе корреляции. Наглядная оценка диаграммы носит, как было указано, предварительный характер. Для более точной оценки зависимости проводится математическая обработка массива парных данных, которая дает численное значение коэффициента корреляции г. Этот математический метод определения корреляции между анализируемыми параметрами называется корреляционным анализом. Математическое определение уравнения зависимости между переменными параметрами называется регрессионным анализом. Вместе с этим следует отметить, что коэффициент корреляции принимает значения в диапазоне -1<г<1. При г, близком к 1(0,8 – 0,95), имеет место сильная корреляция. При г, близком к 0 (0,05 – 0,2), корреляция отсутствует. Можно уверенно считать, что корреляция существует при коэффициенте корреляции г больше 0,6. Если у исследователя есть уверенность в наличии корреляции, а диаграмма рассеивания это не показывает, то целесообразно дополнительно проанализировать собранную информацию на возможность расслоения данных измерения. Возможно, при сборе информации одна из переменных имеет дополнительный стратифицирующий фактор. Например, при определении зависимости силы резания от величины подачи не учли, что обрабатываемые заготовки были изготовлены не из одного материала, а из нескольких. Для оценки эффективности затрат на повышение качества можно так же использовать математический аппарат корреляционного анализа. Исследуя зависимость цены (или рентабельности) от величины издержек, можно по значению коэффициента корреляции этой зависимости оценить целесообразность дополнительных расходов на качество. Временной ряд (или ряд динамики) – собранный в разные моменты времени статистический материал о значении каких-либо параметров (в простейшем случае одного) исследуемого процесса. Каждая единица статистического материала называется измерением или отсчётом, также допустимо называть его уровнем на указанный с ним момент времени. Во временном ряде каждому отчету должно быть указано время измерения или номер измерения по порядку. Временной ряд существенно отличается от простой выборки данных, так как при анализе учитывается взаимосвязь измерений со временем, а не только статистическое разнообразие и статистические характеристики выборки Временной ряд можно рассматривать, как частный случай диаграммы рассеивания, если в качестве переменной по оси X выбрать время, например дни, недели, годы и так далее.  Два типичных вопроса, которые ставятся при анализе временных рядов: наблюдается ли какая – либо устойчивая зависимость от времени в поведении рассматриваемой величины (временной тренд)? наблюдается ли сезонная компонента? 2.3 Понятие о сводке и группировке статистического материала Собранный в процессе статистического наблюдения материал представляет собой разрозненные первичные цифровые сведения об отдельных единицах изучаемого явления. В таком виде материал еще не характеризует явления в целом, так как он слишком разрознен и неклассифицирован. Из него не видно ни состава, ни численности, ни существа связей этого явления с другими. Указанные признаки могут быть получены лишь в процессе обработки материалов наблюдения. Это и является задачей второго этапа статистической работы – сводка и группировка результатов статистического исследования. Статистическая сводка – это систематизация первичных данных и подсчет обобщающих статистических показателей, относящихся ко всей совокупности. Статистическая сводка классифицируется по ряду признаков: по глубине обработки данных: простая; сложная; комбинированная; многомерная; по форме обработки материала: децентрализованная – это способ обобщения материала, который осуществляется снизу доверху по иерархической лестнице управления и на каждом из этапов подвергается обработке; централизованная – это способ, при котором все первичные данные, полученные в результате статистического наблюдения, сосредоточиваются в одной центральной организации и подвергаются обработке от начала до конца; по технике выполнения: механизированная; ручная. Статистическая группировка – это разделение множества единиц изучаемой совокупности на однородные типичные группы по определенным существенным количественным или качественным признакам. Различают следующие виды статистических группировок: типологические – это разделение исследуемой качественно разнородной совокупности на классы, социально – экономические типы, однородные группы единиц; структурные – при группировке этого типа массив данных разбивается на группы, каждая из которых объединяет показатели, характеризующие состояние того или иного структурного элемента изучаемого явления или группы объектов, составляющих это явление; аналитические – это группировка, выявляющая взаимосвязи и взаимозависимости между изучаемыми социально–экономическими явлениями и признаками, их характеризующими. Группированным признаком (основанием группировки) называется признак, по которому проводится разделение единиц совокупности на отдельные группы. Все признаки в статистической науке можно подразделять на: факторные (признаки, которые оказывают большое влияние на изменение результативных признаков); результативные (признаки, изменяющиеся под влиянием факторных признаков). В зависимости от числа положенных в основание группировки признаков различают простые, комбинационные и многомерные группировки. Простой называется группировка, если группа образована только по одному признаку. Если разбить группу на подгруппу в соответствии с определенными признаками, то такую группировку называют комбинированной. Комбинационной считается группировка, когда разбивка совокупности на группы производится по двум и более группировочным признакам, взятым в сочетании (комбинации) друг с другом Комбинационные группировки позволяют изучать единицы совокупности одновременно по нескольким признакам. При изучении сложных социально–экономических явлений и процессов применяются комбинационные группировки. Для того чтобы построить комбинационную группировку, необходимо выявить наличие достаточно большого числа наблюдений. Для того чтобы найти скопление (в мерном пространстве) объектов (точек), необходимо применить многомерную группировку Различают группировки по используемой информации: 1) первичные – производятся на основе исходных данных, которые были получены в результате статистического наблюдения; 2) вторичные – это образование новых групп на основные ранее проведенной группировки. Два способа вторичной группировки: способ укрупнения интервалов; способ деловой перегруппировки. Метод группировок решает следующие задачи статистического анализа: 1. Выделение социально-экономических типов явлений. 2. Изучение структуры явления и структурных сдвигов, происходящих в нем. 3. Обнаружение связи и зависимости между явлениями. Интервалы группировок. При группировке изучаемых явлений по одному признаку, а тем более при комбинации двух-трех признаков можно получить значительное число групп (например, при группировке населения по возрасту, при группировке торговых фирм по числу работников или по размеру товарообороту и т.д.). Для решения вопроса о числе групп необходимо сначала выяснить положение и роль отдельных групп, тенденции их развития и затем выделить характерные, типичные группы, вытекающие из анализа изучаемого явления. Обычно рекомендуется брать не слишком много групп, так как при этом условии в каждую группу входит достаточно большое число единиц, что позволяет выявлять типичное, характерное, а не случайное. Для определения числа групп можно воспользоваться формулой Стерджесса:  где,  – число групп; – число групп; 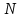 – число единиц совокупности; – число единиц совокупности;  – десятичный логарифм от – десятичный логарифм от 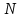 . .Данная формула говорит о том, что выбор числа групп объектно зависит от объема совокупности. После установления числа групп решается вопрос об определении интервалов группировки. Интервал группировки – это интервал значений варьирующего признака, лежащих в пределах определенной группы. Каждый интервал имеет свою длину (ширину), верхнюю и нижнюю границы. Нижняя граница интервала – это наименьшее значение признака в интервале, а верхняя граница интервала – его наибольшее значение. Ширина интервала – это разность между верхней и нижней границами. Величина равного интервала определяется по следующей формуле:  где,  – максимальное и минимальное значение признака в совокупности; – максимальное и минимальное значение признака в совокупности;  – число групп. – число групп.Интервалы группировок могут быть закрытыми и открытыми. Закрытыми интервалами являются интервалы, в которых указаны верхняя и нижняя границы. Открытые интервалы имеют только одну границу (верхнюю – у первого, нижнюю – у последнего). | |||||||||||||||||||||||||||||||
