вышмат. 1. Числоваяпоследовательности и ее предел
 Скачать 0.89 Mb.
|
3.Предел функции. Односторонние пределы.Определение Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами. Левый и правый пределы функцииОпределение Число называется правым пределом функции в точке , если для такое, что для любого и , выполняется неравенство  (рис. 1). Правый предел обозначается  Число называется левым пределом функции в точке , если для такое, что для любого и , выполняется неравенство 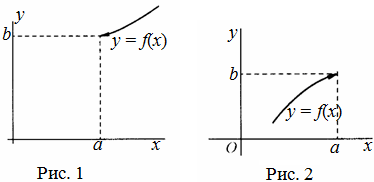(рис. 2). Левый предел обозначается   Левый и правый пределы функции называются односторонними пределами. Теорема Если существуют и , причем  , то существует и  . Обратное утверждение также верно.В случае, если  , то предел  не существует.Задание. Найти односторонние пределы функции при Решение. Правый предел:  Левый предел:  4.Первый замечательный предел.Первый замечательный предел: Определение Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю. Применение первого замечательного предела на практикеПример Задание. Найти предел  Решение. Воспользуемся заменой и первым замечательным пределом. 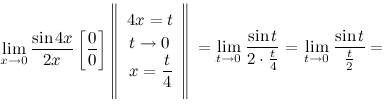  Ответ.  Пример Задание. Найти предел  Решение. Разложим тангенс на синус и косинус и воспользуемся свойствами пределов. 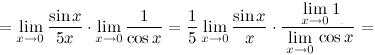   Ответ.  |