вышмат. 1. Числоваяпоследовательности и ее предел
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
8.Таблица производных и правила дифференцирования О том, что такое производная, мы рассказали в статье «Геометрический смысл производной». Если функция задана графиком, её производная в каждой точке равна тангенсу угла наклона касательной к графику функции. А если функция задана формулой — вам помогут таблица производных и правила дифференцирования, то есть правила нахождения производной. 9.Возрастание и убывание функцииОпределение возрастающей функции. Функция y=f(x) возрастает на интервале X, если для любых и Определение убывающей функции. Функция y=f(x) убывает на интервале X, если для любых и 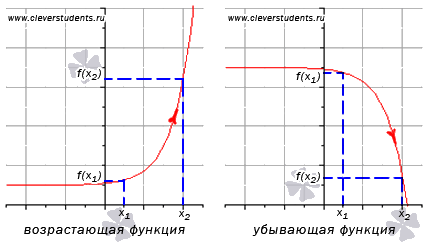 ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a;b), то есть при x=a и x=b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X. К примеру, из свойств основных элементарных функций мы знаем, что y=sinx определена и непрерывна для всех действительных значений аргумента. Поэтому, из возрастания функции синуса на интервале 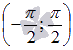 мы можем утверждать о возрастании на отрезке мы можем утверждать о возрастании на отрезке Точки экстремума, экстремумы функции.Точку называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство Точку называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство Под окрестностью точки понимают интервал Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции. 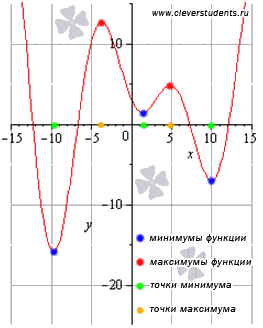 Не путайте экстремумы функции с наибольшим и наименьшим значением функции. 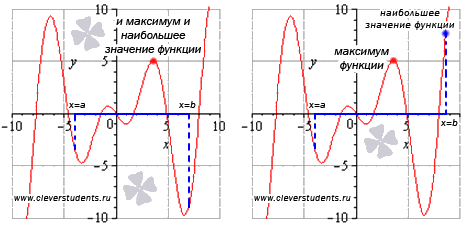 На первом рисунке наибольшее значение функции на отрезке [a;b] достигается в точке максимума и равно максимуму функции, а на втором рисунке – наибольшее значение функции достигается в точке x=b, которая не является точкой максимума. Достаточные условия возрастания и убывания функции.На основании достаточных условий (признаков) возрастания и убывания функции находятся промежутки возрастания и убывания функции. Вот формулировки признаков возрастания и убывания функции на интервале:
Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:
Рассмотрим пример нахождения промежутков возрастания и убывания функции для разъяснения алгоритма. Пример. Найти промежутки возрастания и убывания функции 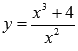 . .Решение. Первым шагом является нахождение обрасти определения функции. В нашем примере выражение в знаменателе не должно обращаться в ноль, следовательно, Переходим к нахождению производной функции: 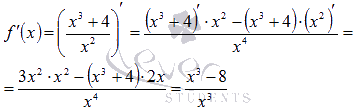 Для определения промежутков возрастания и убывания функции по достаточному признаку решаем неравенства 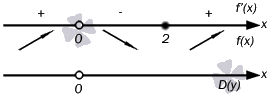 Таким образом, 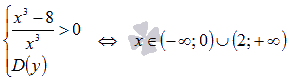 и и 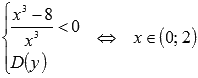 . .В точке x=2 функция определена и непрерывна, поэтому ее следует добавить и к промежутку возрастания и к промежутку убывания. В точке x=0 функция не определена, поэтому эту точку не включаем в искомые интервалы. Приводим график функции для сопоставления с ним полученных результатов. 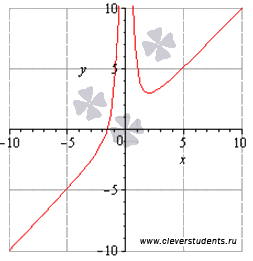 Ответ: функция возрастает при |
