вышмат. 1. Числоваяпоследовательности и ее предел
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
Следствия из первого замечательного предела1° 2° 3° 4° 5.Второй замечательный предел.1 Второй замечательный предел: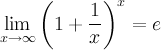 здесь е - число Эйлера. Пример Задание. Найти предел Решение. Подставим , получим неопределенность и для решения предела воспользуемся вторым замечательным пределом. 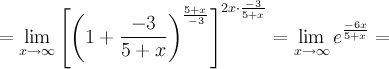 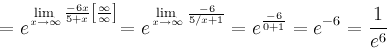 Ответ. Следствия из второго замечательного предела1° 2° 3° 4° 5° 6° 6.Непрерывность элементарных функций Важнейшим свойством всех элементарных функций является их непрерывность в каждой точке определения. Убедимся в этом на примере некоторых элементарных функций.Рациональные функции. 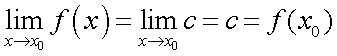 . .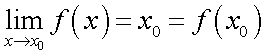 . .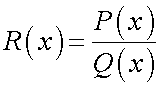 — непрерывна везде, где — непрерывна везде, где 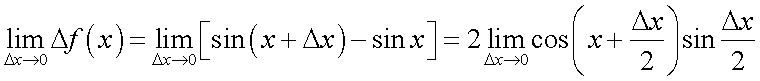 .Так как .Так как 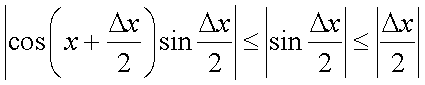 , а последнее выражение стремится к нулю при , а последнее выражение стремится к нулю при 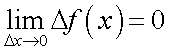 . Неравенство . Неравенство 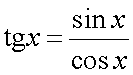 , , 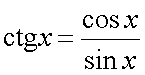 — непрерывны всюду, где знаменатель не обращается в ноль. — непрерывны всюду, где знаменатель не обращается в ноль.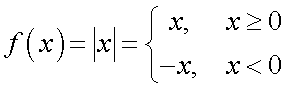 — непрерывна всюду, так как — непрерывна всюду, так как 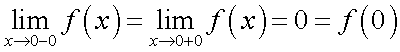 , а непрерывность при , а непрерывность при 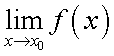 в этой точке может быть вычислен нахождением значения функции в этой точке в этой точке может быть вычислен нахождением значения функции в этой точке 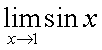 .Поскольку .Поскольку 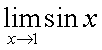 = =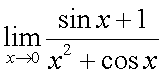 .И в числителе, и в знаменателе стоят непрерывные функции. Поскольку знаменатель отличен от нуля в точке .И в числителе, и в знаменателе стоят непрерывные функции. Поскольку знаменатель отличен от нуля в точке 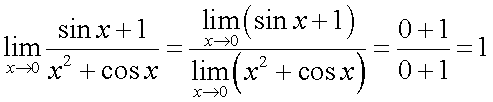 .Пример 3.Найти предел .Пример 3.Найти предел 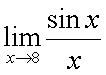 .И в числителе, и в знаменателе стоят непрерывные функции. Поскольку знаменатель отличен от нуля в точке .И в числителе, и в знаменателе стоят непрерывные функции. Поскольку знаменатель отличен от нуля в точке 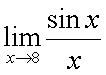 = =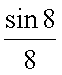 . . |
