вышмат. 1. Числоваяпоследовательности и ее предел
 Скачать 0.89 Mb.
|
11.Производные высших порядков. Формула ТейлораЕсли функция имеет производную в каждой точке своей области определения, то ее производная есть функция от . Функция , в свою очередь, может иметь производную, которую называют производной второго порядка функции (или второй производной) и обозначают символом . Таким образом  Пример Задание. Найти вторую производную функции  Решение. Для начала найдем первую производную:     Для нахождения второй производной продифференцируем выражение для первой производной еще раз:         Ответ.  Больше примеров решенийРешение производных онлайн Производные более высоких порядков определяются аналогично. То есть производная -го порядка функции есть первая производная от производной -го порядка этой функции:  Формула ТейлораФормула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении. Формула Тейлора , где Rn(x) - остаточный член формулы Тейлора. Остаточный член формулы ТейлораВ форме Лагранжа: 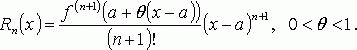 В форме Коши:  12.Неопределенный и определенный интегралыНеопределённый интеграл.Определение. Функция F(x) называется первообразной для функции f(x) на интервале X=(a,b) (конечном или бесконечном), если в каждой точке этого интервала f(x) является производной дляF(x), т.е.  .Из этого определения следует, что задача нахождения первообразной обратна задаче дифференцирования: по заданной функции f(x ) требуется найти функцию F(x), производная которой равна f(x). Первообразная определена неоднозначно: для функции  первообразными будут и функция arctg x, и функция arctg x-10:  . Для того, чтобы описать все множество первообразных функции f(x), рассмотримСвойства первообразной.
Из этих свойств следует, что если F(x) - некоторая первообразная функции f(x) на интервале X, то всё множество первообразных функции f(x) (т.е. функций, имеющих производную f(x) и дифференциал f(x) dx) на этом интервале описывается выражением F(x) + C, где C - произвольная постоянная. Неопределённый интеграл и его свойства. Определение. Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом  .Как следует из изложенного выше, если F(x) - некоторая первообразная функции f(x), то  , где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением.Свойства неопределённого интеграла, непосредственно следующие из определения:
Таблица неопределённых интегралов.
В формулах 14, 15, 16, 19 предполагается, что a>0. Каждая из формул таблицы справедлива на любом интервале, на котором непрерывна подынтегральная функция. Все эти формулы можно доказать дифференцированием правой части. Докажем, например, формулу 4: если x > 0, то  ; если x < 0, то  .Простейшие правила интегрирования.
|
).
.
(или 
).
.
.
.
.
(
).
.
.
.
; 
.
.
.
.
.
.
.
.
.
.
; 
.
(
)