вышмат. 1. Числоваяпоследовательности и ее предел
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
Определённый интегралОпределение определённого интеграла. Пусть на отрезке [a,b] задана функция y = f(x). Разобьём отрезок [a,b] произвольным образом на n частей точками [x0 , x1], [x1 , x2], …, [xi-1 ,xi], …, [xn-1 , xn]; длину i-го отрезка обозначим 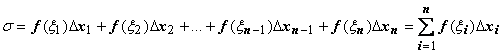 . .Сумма 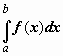 . .Функция f(x), как и в случае неопределённого интеграла, называется подынтегральной, числа a и b - соответственно, нижним и верхним пределами интегрирования. Кратко определение иногда записывают так:  . .В этом определении предполагается, что b> a. Для других случаев примем, тоже по определению: Если b=a, то 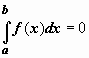 ; еслиb ; еслиbСвойства определённого интеграла. 1. Линейность. Если функции f(x), g(x) интегрируемы по отрезку [a,b] , то по этому отрезку интегрируема их линейная комбинация A f(x) + B g(x) (A, B = const), и 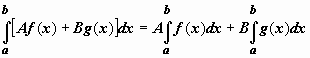 . .2. Аддитивность. Если y = f(x) интегрируема по отрезку [a,b] и точка c принадлежит этому отрезку, то 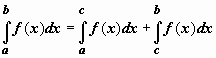 . .При формулировании следующих свойств предполагаем, что b > a. 3. Интеграл от единичной функции ( f(x) = 1). Если f(x) = 1, то 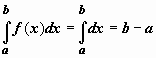 . .Вычисление определённого интеграла. Формула Ньютона-Лейбница. Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции 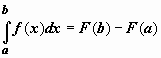 . .Пример применения формулы Ньютона-Лейбница: 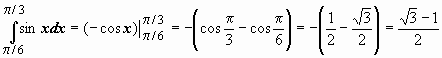 . .Формула интегрирования по частям для определённого интеграла. Если u(x), v(x) - непрерывно дифференцируемые функции, то 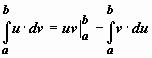 Пример: 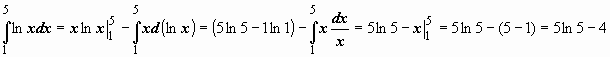 . .13. Геометрический смысл определенного интеграла. Если f(x) непрерывна и положительна на [a, b], то интеграл представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x) (см. рис. 5.). 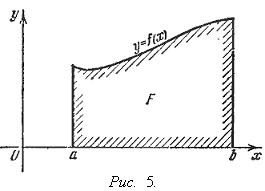 Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции. Пусть, например, функция f(x), заданная на промежутке [a, b], равна нулю во всех точках этого промежутка, кроме конечного числа точек z1, z2, ..., zN. Составим для f(x) интегральную сумму σ. Пусть из точек ξ0, ξ1, ..., ξn-1, входящих в определение σ, p точек совпадают с точками zi, а остальные отличны от них. Тогда в сумме σ будет лишь p слагаемых, отличных от нуля. Если наибольшее из чисел | f(zi) | (i = 1, 2, ...,N) есть K, то, очевидно, | σ | ≤ Kpλ ≤ KNλ, откуда ясно, что при λ → 0 будет и σ → 0. Таким образом, интеграл существует и равен нулю. Приведем теперь пример функции, не имеющей интеграла. Пусть φ(x) задана на промежутке [0, 1] так: 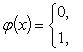 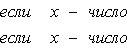 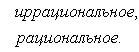 Если мы, составляя сумму σ, за точки ξk выберем числа иррациональные, то окажется σ = 0. Если же все ξk взять рациональными, то получится σ = 1. Таким образом, за счет одного лишь уменьшения λ нельзя приблизить σ к какому-либо постоянному числу, и интеграл не существует. В настоящее время известны точные признаки, позволяющие судить, имеет или нет заданная функция определенный интеграл, но мы ограничимся вышеприведенной теоремой об интегрируемости непрерывных функций. |
