|
|
вышмат. 1. Числоваяпоследовательности и ее предел
21.Дифференциальное уравнение
Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами). Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или все, кроме хотя бы одной производной, отсутствовать вовсе. Не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, 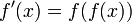 не является дифференциальным уравнением.[ не является дифференциальным уравнением.[
Дифференциальное уравнение порядка выше первого можно преобразовать в систему уравнений первого порядка, в которой число уравнений равно порядку исходного уравнения.
Современные быстродействующие ЭВМ эффективно дают численное решение обыкновенных дифференциальных уравнений, не требуя получения его решения в аналитическом виде. Это позволило некоторым исследователям утверждать, что решение задачи получено, если её удалось свести к решению обыкновенного дифференциального уравнения.
Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения, зависящие от одной независимой переменной; они имеют вид
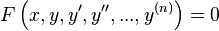 или или 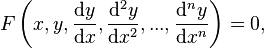
где — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной штрих означает дифференцирование по Число называется порядком дифференциального уравнения. Наиболее практически важными являются дифференциальные уравнения первого и второго порядка.
Порядок дифференциального уравнения
Порядком дифференциального уравнения называют наивысший порядок производной, входящей в данное уравнение.
Простейшие дифференциальные уравнения первого порядка
Простейшие дифференциальные уравнения первого порядка — класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные уравнения первого порядка и линейные уравнения первого порядка. Все эти уравнения можно проинтегрировать в конечном виде.
Отправной точкой изложения будет служить дифференциальное уравнение первого порядка, записанное в т. н. симметричной форме:
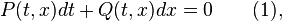
где функции и определены и непрерывны в некоторой области 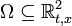 . .
Дифференциальные уравнения в частных производных
Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные. Общий вид таких уравнений можно представить в виде:
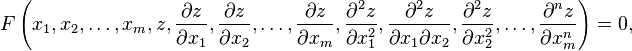
где — независимые переменные, а 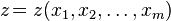 — функция этих переменных. Порядок уравнений в частных производных может определяется так же, как для обыкновенных дифференциальных уравнений. Ещё одной важной классификацией уравнений в частных производных является их разделение на уравнения эллиптического, параболического и гиперболического типа, в особенности для уравнений второго порядка. — функция этих переменных. Порядок уравнений в частных производных может определяется так же, как для обыкновенных дифференциальных уравнений. Ещё одной важной классификацией уравнений в частных производных является их разделение на уравнения эллиптического, параболического и гиперболического типа, в особенности для уравнений второго порядка.
Как обыкновенные дифференциальные уравнения, так и уравнения в частных производных можно разделить на линейные и нелинейные. Дифференциальное уравнение является линейным, если неизвестная функция и её производные входят в уравнение только в первой степени (и не перемножаются друг с другом). Для таких уравнений решения образуют аффинное подпространство пространства функций. Теория линейных ДУ развита значительно глубже, чем теория нелинейных уравнений. Общий вид линейного дифференциального уравнения n-го порядка:
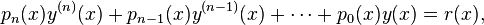
где pi(x) — известные функции независимой переменной, называемые коэффициентами уравнения. Функция r(x) в правой части называется свободным членом (единственное слагаемое, не зависящее от неизвестной функции) Важным частным классом линейных уравнений являются линейные дифференциальные уравнения с постоянными коэффициентами.
Подклассом линейных уравнений являются однородные дифференциальные уравнения — уравнения, которые не содержат свободного члена: r(x) = 0. Для однородных дифференциальных уравнений выполняется принцип суперпозиции: линейная комбинация частных решений такого уравнения также будет его решением. Все остальные линейные дифференциальные уравнения называются неоднородными дифференциальными уравнениями.
Нелинейные дифференциальные уравнения в общем случае не имеют разработанных методов решения, кроме некоторых частных классов. В некоторых случаях (с применением тех или иных приближений) они могут быть сведены к линейным. Например, линейное уравнение гармонического осциллятора 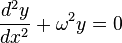 может рассматриваться как приближение нелинейного уравнения математического маятника может рассматриваться как приближение нелинейного уравнения математического маятника 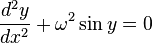 для случая малых амплитуд, когда y ≈ sin y. для случая малых амплитуд, когда y ≈ sin y.
Примеры
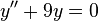 — однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Решением является семейство функций — однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Решением является семейство функций 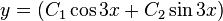 , где и — произвольные константы, которые для конкретного решения определяются из задаваемых отдельно начальных условий. Это уравнение, в частности, описывает движение гармонического осциллятора с циклической частотой 3. , где и — произвольные константы, которые для конкретного решения определяются из задаваемых отдельно начальных условий. Это уравнение, в частности, описывает движение гармонического осциллятора с циклической частотой 3.
Второй закон Ньютона можно записать в форме дифференциального уравнения 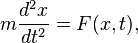 где m — масса тела, x — его координата, F(x, t) — сила, действующая на тело с координатой x в момент времени t. Его решением является траектория движения тела под действием указанной силы. где m — масса тела, x — его координата, F(x, t) — сила, действующая на тело с координатой x в момент времени t. Его решением является траектория движения тела под действием указанной силы.
Дифференциальное уравнение Бесселя — обыкновенное линейное однородное уравнение второго порядка с переменными коэффициентами: 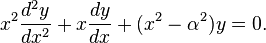 Его решениями являются функции Бесселя. Его решениями являются функции Бесселя.
Пример неоднородного нелинейного обыкновенного дифференциального уравнения 1-го порядка: 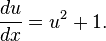
В следующей группе примеров неизвестная функция u зависит от двух переменных x и t или x и y.
Однородное линейное дифференциальное уравнение в частных производных первого порядка:
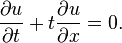
Одномерное волновое уравнение — однородное линейное уравнение в частных производных гиперболического типа второго порядка с постоянными коэффициентами, описывает колебание струны, если — отклонение струны в точке с координатой x в момент времени t, а параметр a задаёт свойства струны:
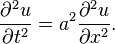
Уравнение Лапласа в двумерном пространстве — однородное линейное дифференциальное уравнение в частных производных второго порядка эллиптического типа с постоянными коэффициентами, возникающее во многих физических задачах механики, теплопроводности, электростатики, гидравлики:
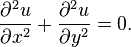
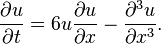
|
|
|
 Скачать 0.89 Mb.
Скачать 0.89 Mb.