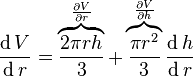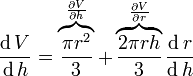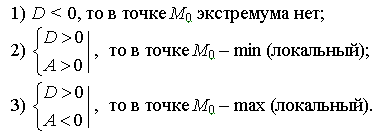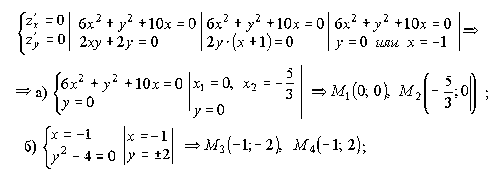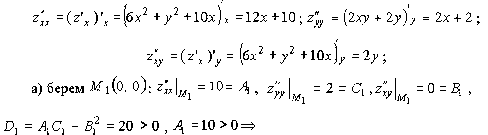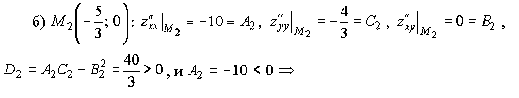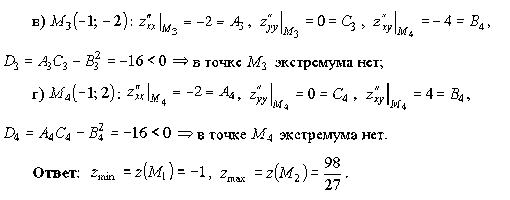вышмат. 1. Числоваяпоследовательности и ее предел

Название	1. Числоваяпоследовательности и ее предел
Анкор	вышмат.docx
Дата	04.05.2017
Размер	0.89 Mb.
Формат файла
Имя файла	вышмат.docx
Тип	Документы #6825
страница	15 из 16

1 ... 8 9 10 11 12 13 14 15 16

19.Частная производная

В математическом анализе частная производная — одно из обобщений понятия производной на случай функции нескольких переменных.
Частная производная — это предел отношения приращения функции по выбранной переменной к приращению этой переменной, при стремлении этого приращения к нулю.

В явном виде частная производная функции в точке 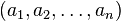$(a_1,a_2,\ldots, a_n)$ определяется следующим образом:

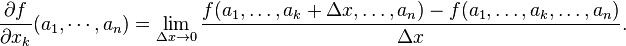
$\frac{\partial f}{\partial x_k}(a_1,\cdots , a_n)=\lim_{\delta x\to 0} \frac{f(a_1,\ldots,a_k+\delta x,\ldots,a_n)-f(a_1,\ldots,a_k,\ldots,a_n)}{\delta x}.$

Обозначение

Следует обратить внимание, что обозначение следует понимать как цельный символ, в отличие от обычной производной функции одной переменной , которую можно представить, как отношение дифференциалов функции и аргумента. Однако, и частную производную можно представить как отношение дифференциалов, но в этом случае необходимо обязательно указывать, по какой переменной осуществляется приращение функции: 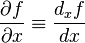$\frac{\partial f}{\partial x} \equiv \frac{d_x f}{d x}$ , где — частный дифференциал функции по переменной . 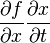Часто непонимание факта цельности символа является причиной ошибок и недоразумений, как, например, сокращение в выражении $\frac{\partial f}{\partial x} \frac{\partial x}{\partial t}$ . ^[1].

Геометрическая интерпретация

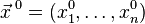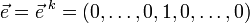Геометрически, частная производная является производной по направлению одной из координатных осей. Частная производная функции в точке $\vec{x}{\,}^0=(x_1^0,\ldots,x_n^0)$ по координате равна производной по направлению $\vec{e}=\vec{e}{\,}^k=(0,\ldots,0,1,0,\ldots,0)$ , где единица стоит на -ом месте.

Примеры

https://upload.wikimedia.org/wikipedia/commons/thumb/d/d2/cone_3d.png/220px-cone_3d.png

Объём конуса зависит от высоты и радиуса основания

Объём V конуса зависит от высоты h и радиуса r, согласно формуле

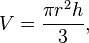
$v = \frac{\pi r^2 h}{3},$

Частная производная объема V относительно радиуса r

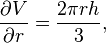
$\frac{ \partial v}{\partial r} = \frac{ 2 \pi r h}{3},$

которая показывает скорость, с которой изменяется объём конуса, если его радиус меняется, а его высота остаётся неизменной. Например, если считать единицы измерения объёма , а измерения длины , то вышеуказанная производная будет иметь размерность скорости измерения объёма , т.е. изменение величины радиуса на 1 м будет соответствовать изменению объёма конуса на .

Частная производная относительно h

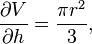
$\frac{ \partial v}{\partial h} = \frac{\pi r^2}{3},$

которая показывает скорость, с которой изменяется объём конуса, если его высота меняется, а его радиус остаётся неизменным.

Полная производная V относительно r и h

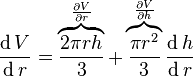
$\frac{\operatorname dv}{\operatorname dr} = \overbrace{\frac{2 \pi r h}{3}}^\frac{ \partial v}{\partial r} + \overbrace{\frac{\pi r^2}{3}}^\frac{ \partial v}{\partial h}\frac{\operatorname d h}{\operatorname d r}$

и

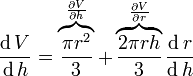
$\frac{\operatorname dv}{\operatorname dh} = \overbrace{\frac{\pi r^2}{3}}^\frac{ \partial v}{\partial h} + \overbrace{\frac{2 \pi r h}{3}}^\frac{ \partial v}{\partial r}\frac{\operatorname d r}{\operatorname d h}$

Различие между полной и частной производной — устранение косвенных зависимостей между переменными в последней.

Если (по некоторым причинам) пропорции конуса остаются неизменными, то высота и радиус находятся в фиксированном отношении k,

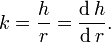
$k = \frac{h}{r} = \frac{\operatorname d h}{\operatorname d r}.$

Это даёт полную производную относительно r:

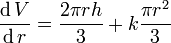
$\frac{\operatorname dv}{\operatorname dr} = \frac{2 \pi r h}{3} + k\frac{\pi r^2}{3}$

20. Экстремум функции двух переменных

Определение 1.11 Пусть задана функция двух переменных z=z(x,y), (x,y)D. ТочкаM₀(x₀;y₀) - внутренняя точка области D.

Если в D присутствует такая окрестность UM₀ точки M₀, что для всех точек

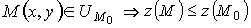
то точка M₀ называется точкой локального максимума. А само значение z(M₀) - локальным максимумом.

А если же для всех точек

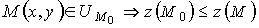
то точка M₀ называется точкой локального минимума функции z(x,y). А само значение z(M₀) - локальным минимумом.

Локальный максимум и локальный минимум называются локальными экстремумами функции z(x,y). На рис. 1.4 поясняется геометрический смысл локального максимума: M₀ - точка максимума, так как на поверхности z =z (x,y) соответствующая ей точка C₀ находится выше любой соседней точки C (в этом локальность максимума).

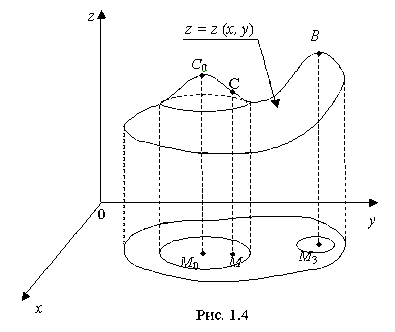
http://vm.psati.ru/online-math-sem-2/pics/1-9-092.gif

Заметим, что на поверхности в целом есть точки (например, В), которые находятся выше C₀, но эти точки (например, В) не являются "соседними" с точкой C₀.

В частности, точке В соответствует понятие глобального максимума:

Аналогично определяется и глобальный минимум:

Нахождение глобальных максимумов и минимумов будет рассмотрено в п.1.10.

Теорема 1.3(необходимые условия экстремума).

Пусть задана функция z =z (x,y), (x,y)D. Точка M₀(x₀;y₀D - точка локального экстремума.

Если в этой точке существуют z'_x и z'_y, то

http://vm.psati.ru/online-math-sem-2/pics/1-9-095.gif

Геометрическое доказательство "очевидно". Если в точке C₀ на (рис.1.4) провести касательную плоскость, то она "естественно" пройдет горизонтально, т. е. под углом 0° к оси Ох и к оси Оу.

Тогда в соответствии с геометрическим смыслом частных производных (рис.1.3):

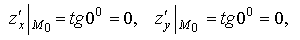
что и требовалось доказать.

Определение 1.12.

Если в точке M₀ выполняются условия (1.41), то она называется стационарной точкой функции z (x,y).

Теорема 1.4(достаточные условия экстремума).

Пусть задана z =z (x,y), (x,y)D, которая имеет частные производные второго порядка в некоторой окрестности точки M₀(x₀,y₀)D. Причем M₀ - стационарная точка (т. е. необходимые условия (1.41) выполнены). Вычислим:

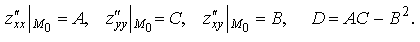
Если:

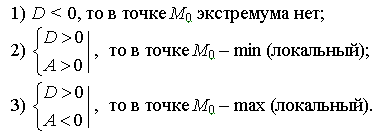
http://vm.psati.ru/online-math-sem-2/pics/1-9-098.gif

Доказательство теоремы использует темы (формула Тейлора функции нескольких переменных и теория квадратичных форм), которые в этом пособии не рассматриваются.

Пример 1.13.

Исследовать на экстремум:

Решение

1. Найдём стационарные точки, решая систему (1.41):

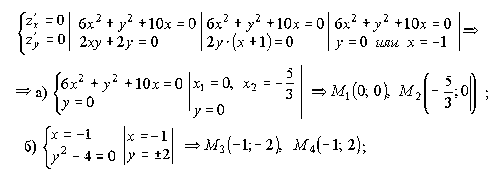
http://vm.psati.ru/online-math-sem-2/pics/1-9-100.gif

то есть найдены четыре стационарные точки.
2.

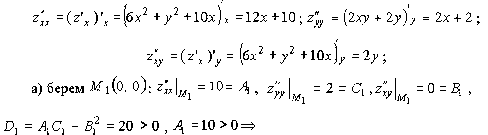
http://vm.psati.ru/online-math-sem-2/pics/1-9-101.gif

по теореме 1.4 в точке – минимум.

Причём

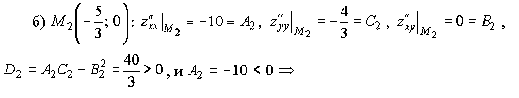
http://vm.psati.ru/online-math-sem-2/pics/1-9-104.gif

по теореме 1.4 в точке

- максимум.
Причём

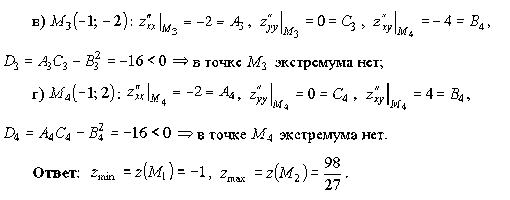
http://vm.psati.ru/online-math-sem-2/pics/1-9-107.gif

1 ... 8 9 10 11 12 13 14 15 16