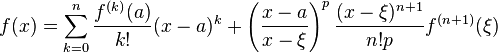вышмат. 1. Числоваяпоследовательности и ее предел

Название	1. Числоваяпоследовательности и ее предел
Анкор	вышмат.docx
Дата	04.05.2017
Размер	0.89 Mb.
Формат файла
Имя файла	вышмат.docx
Тип	Документы #6825
страница	13 из 16

1 ... 8 9 10 11 12 13 14 15 16

Связанные определения

В случае, если , этот ряд также называется рядомМаклорена.

Свойства

Если есть аналитическая функция в любой точке , то её ряд Тейлора в любой точке области определения сходится к в некоторой окрестности .
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности . Коши предложил такой пример:

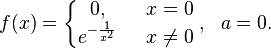
$f(x)= \left\{ \begin{matrix} 0,&\ \ x=0\\ e^{-\frac{1}{x^2}} &\ \ x\not=0 \end{matrix} \right.,\ \ a=0.$

У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке равны нулю.

Формула Тейлора

Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.

Теорема:

Пусть функция имеет производную в некоторой окрестности точки ,
Пусть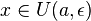 $x\in u(a, \epsilon)$
Пусть — произвольное положительное число,

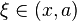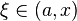тогда: точка $\xi\in (x,a)$ при или $\xi\in (a,x)$ при a" ALIGN=BOTTOM WIDTH=47 HEIGHT=12 BORDER=0>:

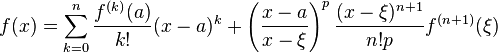
$f(x) = \sum_{k=0}^n {f^{(k)} (a) \over k!} (x - a)^k + \left({x - a \over x - \xi}\right)^p{(x - \xi)^{n+1}\over n! p}f^{(n+1)}(\xi)$

Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха —Роша).

Различные формы остаточного члена

В форме Лагранжа:

$r_{n+1}(x) = {(x - a)^{n+1} \over (n+1)!}f^{(n+1)} [a + \theta(x - a)] \qquad p = n+1; \qquad 0 < \theta < 1$

В форме Коши:

$r_{n+1}(x) = {(x - a)^{n+1} (1 - \theta)^n \over n!}f^{(n+1)} [a + \theta(x - a)] \qquad p = 1; \qquad 0 < \theta < 1$

В интегральной форме:

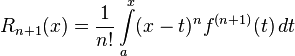
$r_{n+1}(x) = {1 \over n!}\int\limits_a^x (x-t)^n f^{(n+1)} (t)\,dt$

Ослабим предположения:

Пусть функция имеет производную в некоторой окрестности точки
И производную в самой точке , тогда:

В асимптотической форме (форме Пеано, локальной форме):

$r_{n+1}(x) = o[(x - a)^n ]</h2>$

Формула Тейлора для функции двух переменных

Пусть функция имеет полные производные вплоть до -го порядка включительно в некоторой окрестности точки . Введём дифференциальный оператор

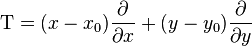$\mathrm{t}=(x-x_0)\dfrac {\partial} {\partial x}+(y-y_0)\dfrac {\partial} {\partial y}$ .

Тогда разложением в ряд Тейлора функции по степеням и в окрестности точки будет

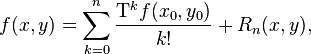
$f(x,y)=\sum\limits_{k=0}^n \dfrac {\mathrm{t}^k f(x_0,y_0)} {k!} + r_n(x,y),$

где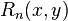

— остаточный член в форме Лагранжа:

$r_n(x,y)=\dfrac {\mathrm{t}^{(n+1)} f(\xi,\zeta)} {(n+1)!},\ \xi \in [x_0,x],\ \zeta \in [y_0,y]$

В случае функции одной переменной 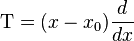$\mathrm{t}=(x-x_0)\dfrac d {dx}$ , поскольку для функции одной переменной частная производная тождественно равна полной. Аналогично формула распространяется на функции от любого числа переменных, меняется только число слагаемых в операторе .

1 ... 8 9 10 11 12 13 14 15 16