Шпоры по матану(1 курс). 1. Функция, одз
 Скачать 0.69 Mb.
|
2.Произведение бесконечно малой функции на ограниченную есть снова бесконечно малая функция.8. Свойства предела функции.1. Функция f(x) в точке х0 может иметь только один предел. Доказательство: Пусть (1) и одновременно где a≠b. (2) Тогда для любой последовательности { хn} сходящейся к х0 (где все хn≠ х0), мы должны иметь два предела   что невозможно, т.к. последовательность {f(хn)} может иметь только один предел. 2.Если f(x) имеет предел в точке, то в некоторой окрестности этой точки функция ограничена. Доказательство. Предположим, что это не так. U1=( х0-ε ; х0+ε), ε>0 . Ввиду неограниченности f(x) в этой окрестности должна найтись точка х1 U1 , такая что │f(х1)│>1. Уменьшим вдвое эту окрестность и рассмотрим U2=( х0-ε/2 ; х0+ε/2), ε>0 окрестность, в ней снова найдется такая точка х2 U2 , такая что │f(х2)│>2. Продолжив это рассуждение, получим Un=( х0-ε/n ; х0+ε/n) , f(хn) > n, хn → х0 ; f(хn)→∞. мы пришли к противоречию. 3.Если для всех точек х некоторой окрестности точки х0 выполняется неравенство f(x) ≥b , то и если такой предел существует. (доказывается по соответствующему свойству предела числовой последовательности). 4  .Если в некоторой окрестности точки х0 имеем f(x)≥g(x) , то и если пределы существуют.5  . Если в некоторой окрестности точки х0 имеем f(x)≥g(x)≥h(x) причем пределы f(x) и h(x) при х→ х0 существуют и равны между собойАрифметические свойства пределов. 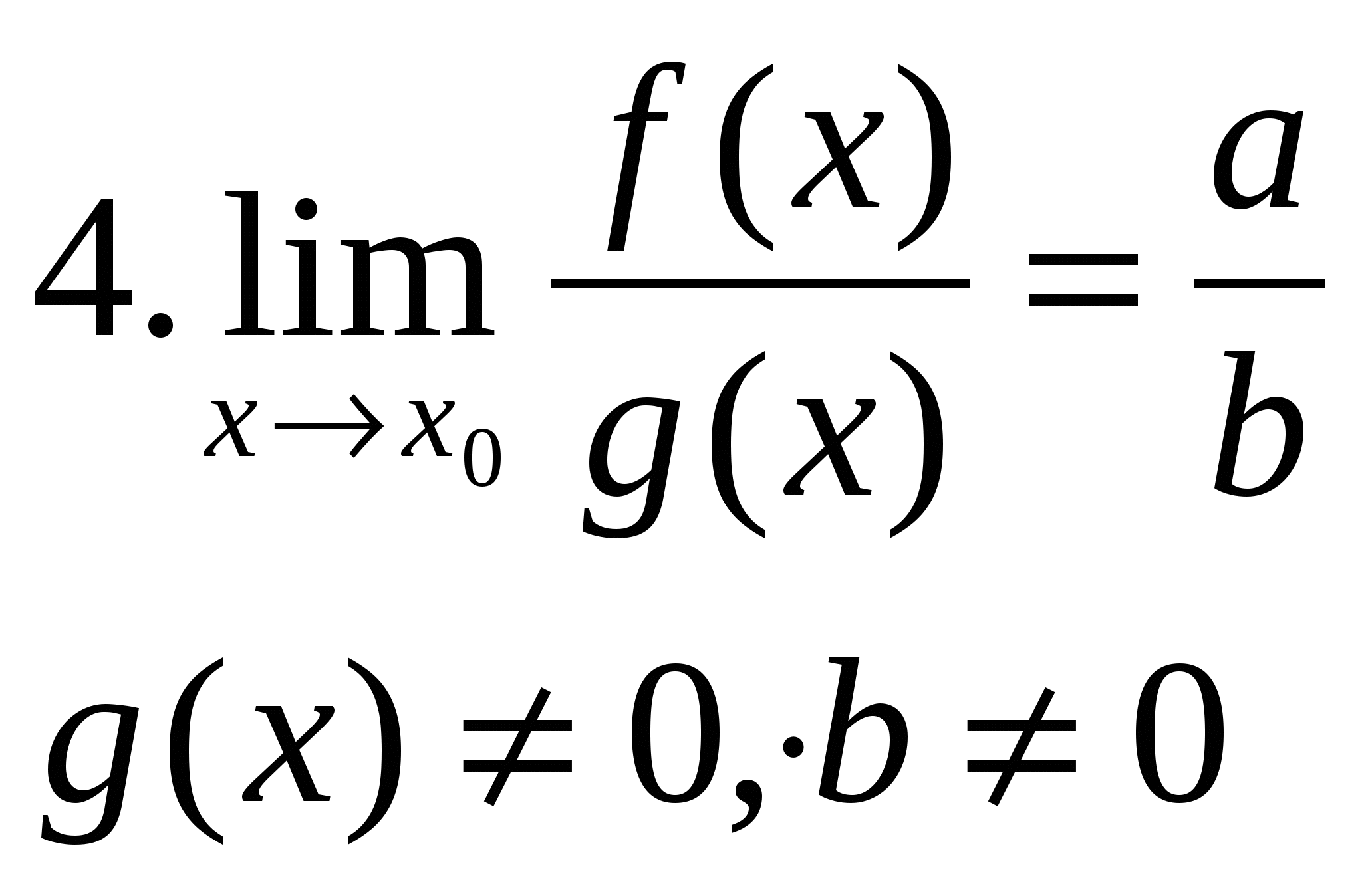      9. Односторонние пределы.О  пр.Число а называют пределом функции f(x)в точке х0 справа, если для любой сходящейся к х0 последовательности {хn}, в которой все хn>х0, соответствующая последовательность {f(хn)} сходится к а. Аналогично определяют предел функции слева: 10. Асимптоты функций.Прямая у=а называется вертикальной асимптотой графика у=f(x) , если хотя бы один из пределов  П  рямая у=кх+b является наклонной асимптотой графика у=f(x) при х→+∞, если f(x) представима в виде f(x)= кх+b+α(х), где Теорема. Для того чтобы график функции у=f(x) имел х→+∞ наклонную асимптоту , необходимо и достаточно, чтобы существовали два предела Аналогично определяется наклонная асимптота для случая х→-∞. 11 Монотонные функции.Функция y=f(x) называется возрастающей (убывающей) на некотором множестве Х принадл. R1, если она определена на этом множестве и если для любых значений х1, х2, принадлежащим Х, из условия х1<х2 следует нер-во: f(x1) Функция y=f(x) называется неубывающей (невозрастающей) на некотором множестве Х принадл. R1, если она определена на этом множестве и если для любых значений х1, х2 принадлежащим Х из условия х1<х2 следует нер-во: f(x1)≤f(x2) (f(x1) ≥f(x2)) Невозрастающие, неубывающие, возрастающие и убывающие ф-и наз. Монотонными. Любая ограниченная монотонная функция имеет предел. |