Шпоры по матану(1 курс). 1. Функция, одз

• Название: 1. Функция, одз
• Анкор: Шпоры по матану(1 курс).doc
• Дата: 25.03.2018
• Размер: 0.69 Mb.
• Имя файла: Шпоры по матану(1 курс).doc
• Тип: Документы; #17195
• страница: 33 из 33

5. Статистические оценки: несмещенные, эффективные, состоятельные

Рассматривая x₁, x₂, … , x_n как независимые случайные величины

X₁, X₂, … , X_n, можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения – это значит найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра.

Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.

Пусть Θ* - статистическая оценка неизвестного параметра Θ теоретического распределения.

Несмещенной называют статистическую оценку Θ*, математическое ожидание которой равно оцениваемому параметру Θ при любом объеме выборки, т. е.

М(Θ*) = Θ.

Возможные значения Θ* могут быть сильно рассеяны вокруг своего среднего значения, т. е. дисперсия D (Θ*) может быть значительной  существует возможность допустить большую ошибку. По этой причине к статистической оценке предъявляется требование эффективности.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.

Состоятельной называют статистическую оценку, которая при n   стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n   стремится к нулю, то такая оценка оказывается и состоятельной.

6. Точность и надежность оценки

Пусть найденная по данным выборки статистическая характеристика Θ* служит оценкой неизвестного параметра Θ. Если Δ > 0 и  Θ – Θ* < Δ, то чем меньше Δ, тем оценка точнее. Таким образом, положительное число Δ характеризует точность оценки.

Надежностью (доверительной вероятностью) оценки Θ по Θ* называют вероятность , с которой осуществляется неравенство  Θ – Θ* < Δ. Обычно надежность оценки задается наперед, причем в качестве  берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.

Доверительным называют интервал (Θ* - Δ, Θ* + Δ), который покрывает неизвестный параметр с заданной надежностью .

Для определения необходимой численности выборки нужно задать уровень точности выборочной совокупности (Δ) с определенной вероятностью (). Ф ((Δ√n ) / σ) =  / 2  можно найти значение t = (Δ√n ) / σ  n = (t²σ²)/Δ²

7. Понятие о критериях согласия. Проверка гипотез о равенстве долей и средних. Проверка гипотезы о виде распределения.

Статичтической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений. Нулевой (основной) называют выдвинутую гипотезу Н₀. Конкурирующей (альтернативной) называют гипотезу Н₁, которая противоречит нулевой. Правило, по которому принимают решение о том, принять или отклонить гипотезу Н₀, называют критерием. Обычно критерием служит некая случайная величина, вычисляемая по выборке. (Критерием согласия называют критерий проверки гипотезы о предполагаемом законе не известного распределения.)

В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т.е. могут быть допущены ошибки двух родов: 1)ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза; 2) ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Вероятность совершить ошибку первого рода принято обозначать через . Её называют уровнем значимости.

Статичтическим критерием называют величину К, которая служит для проверки нулевой гипотезы.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают. Облать принятия гипотезы – совокупность значений критерия, при которых гипотезу принимают. Основной принцип проверки статистических гипотез: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают.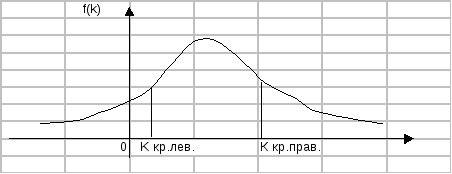


облать значений К разбивается на две подоблати: подоблать принятия нулевой гипотезы (К кр.лев; К кр.прав); подобласть отклонения гипотезы Н₀.

Из определения уровня значимости следует, что = ^{К кр.лев} f(k)dk+^+f(k)dk

^{- К кр.прав.}

Если плотность распределения К симметрична относительно оси ординат,то

^+f(k)dk=/2. Если f(k) и  известны, то можно найти К кр.прав.

^{К кр.прав.}

Проверка гипотезы по равенству математических ожиданий нормально распределённых совокупностей при известных дисперсиях.

Пусть Х – нормально распределённая случайная величина с неизвестным М(х)=а_х и известной D(x)=G²_x ; Y - нормально распределённая случайная величина с неизвестным М(х)=а_у и известной D(x)=G²_y

В результате проведённого эксперимента вычисляется х_{средняя} и у_{средняя.}

Выдвигаем гипотезу Н₀: а_х=а_у и конкурирующую гипотезу Н₁: а_х не равно а_у.

Требуется оценить нулевую гипотезу с уровнем значимости .

Решение.

Х_cр. распределена по нормальному закону  М(х)=а_х и D(x)=G²_x/n. У_ср. распределена по нормальному закону  М(у)=а_у и D(у)=G²_y/m

Х_ср.-У_ср. распределена по нормальному закону  М(х-у)=0 и D(x-у)=G²_x/n+G²_y/m. Введём случайную величину К= Х_{ср .}- У _ср.

 G²_x/n+G²_y/m К имеет нормальное распределение с М(к)=0 и D(k)=1.  нормальное распределение симетрично ^+f(k)dk=/2=0,5-Ф(К кр.прав.)

^{К кр.прав.}

Далее находим по таблицам фукнции Лапласса К кр.прав. Далее находим Кнабл. Затем: 1) Если Кнабл.[Ккр.лев; К кр.прав.], то гипотеза Н₀ принимается. 2) если Кнабл{критическая область}, то гипотеза Н₀ отвергается.

Проверка гипотезы о равенстве математическом ожидании нормально распределённой случайной величины при равных неизвестных диспрерсиях.

Пусть Х – нормально распределённая случайная величина с неизвестным М(х)=а_х и D(x)=G² ; Y - нормально распределённая случайная величина с неизвестным М(х)=а_у и D(x)=G²

В результате проведённого эксперимента вычисляется х_{средняя} и у_{средняя.}

Выдвигаем гипотезу Н₀: а_х=а_у и конкурирующую гипотезу Н₁: а_х не равно а_у.

Требуется оценить нулевую гипотезу с уровнем значимости .

Решение.

Построим К.

_n . _n .

S²_x=((x_i-x)²)/(n-1), S²_y=((y_i-y)²)/(n-1).

^{i=1 i=1}

Х – случайная величина, распределённая по нормальному закону с числовыми характеристиками (а_х, G/n). Y – случайная величина, распределённая по нормальному закону с числовыми характеристиками (а_y, G/m)

Оказывается случайная величина S²_x и S²_y имеют распределение ²(«хи-квадрат») со степенями свободы (n-1) и (m-1).

Введём случайную величину U=((n-1)S²_x)/G²+((m-1)S²_y)/G² имеет распределение ² с числом степеней свободы n+m-2.

Случайная величина Х-У имеет нормальный закон распределения с характеристиками (а_х-а_у, G²/n+G²/m^)

Поэтому нормализированная случайная величина

U = (х-у)-(а_х-а_у)

G²/n+G²/m^

Имеет нормальное распределение N(0,1), а отношение

V = ( x- y) –(a_x-a_y) .

U/(m+n-2)^ 1/m+1/n^[(m-1)S²_x/²+(n-1)S²_y/²]_*1/(m+n-2)

имеет распределение Стьюдента с (m+n-2) степенями свободы. Таким образом можно найти Кнабл.

Кнабл. =(х-у)/(1/m+1/n)_*[(m-1)S²_x+(n-1)S²_y]/(m+n-2)^

Имеет распределение Стьдента с (m+n-2) степенями своды. Далеее вывод делается как в предыдудей задаче.

8. распределение ²

Распределение ² – закон распределения непрерывной случайной величины, плотность которой определяется формулой.

f _² (x)=  1_* e^-x/2x^(k/2)-1, x>0

2^k/2Г(k/2)

0, x0 _

чило к=n-1 - число степеней свободы. Г(х) – гамма-функция Г(х)= t^x-1e^-tdt

⁰

C увеличением степеней свободы распределение медленно приближается к нормальному. Причём для f _² (x) М{ }=n, D{ }=n²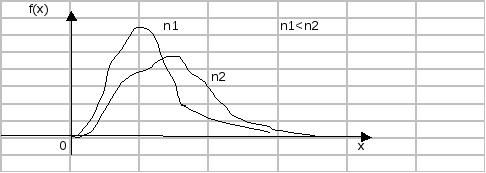



Для дальнейшего «въезжания» необходимо иметь хотя бы отдаленное представление о следующих понятиях

9. Распределение Стьюдента ( или t-распределение) .

Пусть Z – нормальная случайная величина, причём M(Z)=0, (Z)=1, а V – независимая от Z величина, которая распределена по закону ² с к степенями свободы. Тогда величина Т= Z

V/k^

(отношение нормированной нормальной величины к квадратному корню из независимой случайной величины, которая распределена по закону ² с к степенями свободы, делённой на к, распределено по закону Стьюдента с к степенями свободы.)

10. Распределение F Фишера – Снедекора.

Если U и V- независимые случайные величины, распределённые по закону ² со степенями свободы к₁ и к₂, то величина F=U/k₁

V/k₂

имеет распределение, которое называется распределением F Фишера-Снедекора со степенями свободы к₁ и к₂ (иногда его обозначают через V²)

Плотность распределения. f(x) =Г((m+n)/2)_*m^m/2_*n^n/2 _* x^n/2-1

Г(m/2)_*Г(n/2) (m+nx)^(m+n)/2, x>0

При больших m и n переходит в нормальное распределение. Число степеней свободы k₁=n-1,k₂=m-1.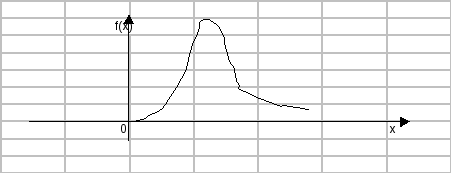



(cправка закончена)

11. Проверка аналитических гипотез

1. Сравнение двух средних норм генеральных совокупностей, дисперсии коттрых известны.

2. Сравнение двух средних нормальных генеральных совокупностей, дисперсии, которых неизвестны и одинаковы.

Дано Х и У – случайные величины с нормальными распределениями.

Найдены Хср. и Уср. Известно – G²_x=G²_y=G²

MX=MY при конкурирующей гипотезе. Н₁: МХ не равно МУ с уровнем значимости .

Схема решений.

1. Находим S²_x и S²_y - исправленные выборочные.

2. Вычисляем набд=людаемое значение критерия

Т= ( x- y) _* mn(m+n-2)

(n-1)S²_x+(m-1)S²_Y  m+n

Оказывается критерий Т –случайная величина распределения Стьюдента.

3. По заданному уровню значений  и числу степеней свободы k=m+n-2 по таблице критических точек распределения Стьюдента находим критическое значение параметра Ткр. (, к)

4. Сравниваетм Ткр. И Тнабл., делаем вывод:

а) если |Тнабл.|< Ткр.(, к), то нет оснований отвергнуть Н₀.

б) если |Тнабл.|>Ткр.(, к), то гипотезу отвергаем.

3 . Сравнение двух дисперсий нормальных генеральных совокупностей.

Х и У – нормальные генеральные совокупности. По выборкам найдены S²_x и S²_y Требуется проверить гипотезу Н₀: DX=DY при конкурирующей гипотезе Н₁ а) DX>DY б)DX не равно DY.

Схема решение в случае а).

1. Вычисляется наблюдаемое значение критерия. Fнабл.= S²_{больша е}/ S²_{меньшая} =S²_x/ S²_y. Оказывается, что F – случайная величина, распределённая по закону Фишера-Снедекора.

2.По заданному уровню значимости  и числу степеней свободы k₁=n-1,k₂=m-1 находим критическую точку Fкр. (,k₁,k₂) k₁ – число степеней свободы большей дисперсии,k₂ - число степеней свободы меньшей дисперсии.

3.Сравнивая Fкр. и Fнабл. ,делаем вывод: Если Fкр. < Fнабл., то гипотезу Н₀ принимаем, если Fкр. > Fнабл., то гипотезу отвергаем.

Схема решения в случае б) аналогична,только в №2 F(/2,k₁,k₂), в №3 k₁=n-1,k₂=m-1 или k₂=n-1,k₁=m-1 , так как k₁ – число степеней свободы большей дисперсии,k₂ - число степеней свободы меньшей дисперсии.
Проверка статистической гипотезы о виде закона распределения (Критерий Пирсона).

Х – случайная величина. Требуется но уровню значимости  проверить гипотезу о нормальном распределении Х.

Схема решения.

1. Весь интервал выборочных значений разделить на S частных интервалов одинаковой длины. Находим середины частичных интервалов, переходим к новому выборочному распрелению. n_i –число фактических зачений попавших в i интервал.

2. Для получения последовательности равностоящих вариантов находим

X^* ср =(^S_i=1n_ix_i)/n, G^*=n_i*(x_i-x^*)²/n^.

попадания х в i интервал. Если х – нормально распределённая случайная величина, то Z распределена по нормальному закону с нулевым математическим ожиданием и единичной дисперсией и p_i=Ф(Z_i+1) – Ф(Z_i), а Z_i=(x_i-x^*)/G^*

3. Нормируем случайную величину х, рассматриваетм величину Z=(x-x^*)/G^*

4. вычисляем теоретические (вычисленные в предположении нормального распределения) частоты n_i =n_*p_i ,p_i - веростность
5. В качестве проверки нулевой гипотезы применим критерий Пирсона.

²=^s(n_i-n_i)<sup>2

i=1</sup> n_i

6. По таблиые критических точек распределения ² по заданному уровню значимости  и числу степеней свободы k=s-3 находим критическую точку ²_кр.(,к).

7. Сравнивая ²_кр. и ²_набл., делаем вывод: - если ²_набл.< ²_кр. , то гипотезу о нормальном распределении Х принимаем (с уровнем значимости )

- если ²_набл.> ²_кр. , то гипотезу о нормальном распределении Х отвергаем.

(Аналогично проверяется,что гипотеза принадлежит любому другому распределению, только в № 4 р_i будет считаться в соответствии с этим распределением.)