Шпоры по матану(1 курс). 1. Функция, одз

• Название: 1. Функция, одз
• Анкор: Шпоры по матану(1 курс).doc
• Дата: 25.03.2018
• Размер: 0.69 Mb.
• Имя файла: Шпоры по матану(1 курс).doc
• Тип: Документы; #17195
• страница: 32 из 33

18. Неравенства Маркова и Чебышева. Закон больших чисел. Теоремы Бернулли и Чебышева. Центральная предельная теорема Ляпунова.

Неравенство Маркова . Пусть У  - дискретная СВ.  - некоторое число, тогда Р(У) ≤М(У)\ 

Неравенство Чебышева. Пусть имеется СВ  с математическим ожиданием m и дисперсией D. Каково бы ни было положительное число , вероятность того, что величина  отклонится от своего математического ожидания не меньше чем на , ограничена сверху числом D\²

Под законом больших чисел в теории вероятностей понимается ряд теорем, в каждой из которых устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным.

Теорема Чебышева. Пусть имеется бесконечная последовательность 1,2,.. независимых случайных величин с одним и тем же математическим ожиданием m и дисперсиями, ограниченными одной и той же постоянной:

M[1]=M[2]=…=m

D[1]
Тогда каково бы ни было положительное число , вероятность события

|((1+…+n)\n)-m|<, стремится к 1 при n стремящемся к бесконечности.

Теорема Бернулли. Пусть производится n независимых опытов, в каждом из которых с вероятностью р может наступить некоторое событие А. Рассмотрим СВ  - число наступлений события А в n опытах. Каково бы ни было положительное число , вероятность события

|\n-p|< стремится к 1 при n стремящемся к бесконечности.

Центральная предельная теорема Ляпунова.

Е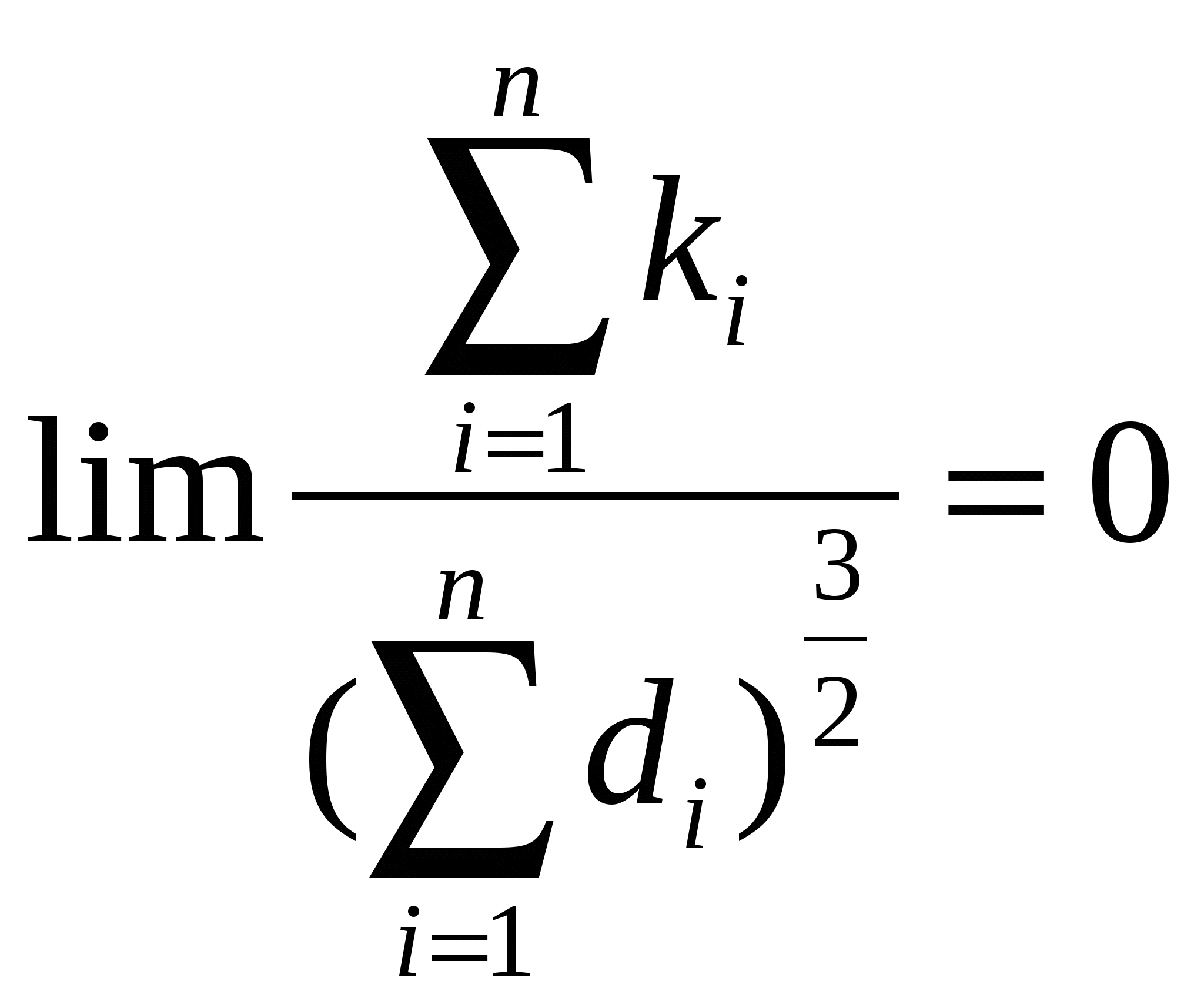сли последовательность 1,2,..независимых СВ удовлетворяет условию Ляпунова (отдельные отклонения i от ее математического ожидания должны быть равномерно малы по сравнению с суммарным отклонением случайных величин. Если при n стремящемся к бесконечности предел

то будем говорить, что последовательность

1,2,..удовлетворяет условию Ляпунова)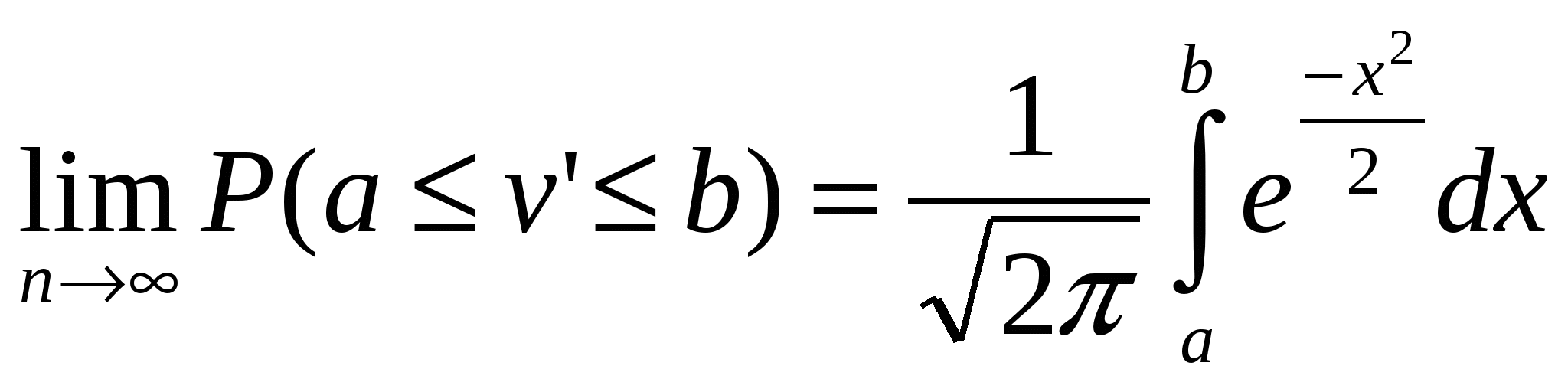

то справедливо предельное соотношение


что означает, что закон распределения СВ v' с ростом приближается к нормальному с мат. ожиданием 1 и дисперсией 0.

8. Математическая статистика.

1. Генеральная совокупность и выборка. Вариационный ряд. Гистограмма,

Опр.1. Выборкой наз совокупность случайно отобранных объектов.

Опр.2 Генеральной совокупностью наз совокупность объектов, из которых производится выборка. Объемом сов-ти наз число объектов этой совокупности.

Опр.3. Ряд распределения – это упорядоченное распределение единиц совокупности на группы по к.-л. признаку. Вариационным рядом (в.р.) наз группировка сов-ти по количественному признаку, т.е. это ряд распределения, сгруппированный по колич. Признаку.

В.Р. будет дискретным, если он остроен подискретному признаку и непрерыным, если – по непрерывному.

В случае непрерывного признака целесообразно строить гистограмму. На оси Ох строятся интервалы, над которыми строятся прямоугольники с высотой, равной частоте (относительной частоте) соответствующего интервала.


Площадь гистограммы равна сумме всех частот, т.е. объему выборки.( в случае относительных частот = 1).

2. Эмпирическая ф-я распределения.(э.ф.р.)

Опр. Э.Ф.Р. (ф-й распределения выборки) наз ф-ю F*(х), определяющую для каждого значения х относительную частоту события Х<х: F*(х)=n_x/n, n_{x –}число вариант, меньших х, n- объем выборки.

3. Выборочная средняя

Опр. Выборочной средней Хв(над Х необходимо рисовать черточку) наз среднее арифметическое значение признака выборочной совокупности. Если все значения х₁,х₂,…,х_n различны, то

Хв=(х1+х2+…+ х_n)/n.

Если значения признака х₁,х₂,…,х_k имеют соответственно частоты n₁,n₂,…,n_k, причем n₁+n₂+…+n_k =n, то

Хв=(∑_i=1^kn_ix_i)/n, т.е. выборочная средняя есть средняя взвешанная значений признака с весами, равными соответствующим частотам.

4. Выборочная дисперсия.

Выборочной дисперсией Dв наз среднее арифметическое квадратов отклонений наблюдаемых значений признака от их среднего значения Хв (с чертой).

Если все значения х₁,х₂,…,х_n различны, то

Dв=(∑_i=1ⁿ(x_i – x_в )²)/n

Если значения признака х₁,х₂,…,х_k имеют соответственно частоты n₁,n₂,…,n_k, причем n₁+n₂+…+n_k =n, то Dв=(∑_i=1^kn_i(x_i – x_в )²)/n, т.е. выборочная дисперсия есть средняя взвешанная квадратов отклонений с весами, равными соответствующим частотам.