автматика. 1. Описание принципа действия выбранной конструкции следящей системы автоматического регулирования сар 5
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
7.Анализ качества исходной САР по частотным характеристикамЕсли на вход динамического звена подать сигнал вида x(t)=Aвхsin 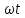 или в форме Эйлера x(t)=Aвхеjωt, то выходной сигнал будет иметь вид у(t)=Aвых(sin или в форме Эйлера x(t)=Aвхеjωt, то выходной сигнал будет иметь вид у(t)=Aвых(sin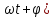 или в форме Эйлера у(t)=Aвыхеj(ωt+φ). Отношение выходного сигнала к входному называется частотной передаточной функцией: или в форме Эйлера у(t)=Aвыхеj(ωt+φ). Отношение выходного сигнала к входному называется частотной передаточной функцией: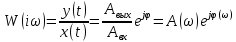 , ,где А(ω) – модуль частотной передаточной функции (отношение амплитуд входного и выходного сигналов) φ(ω) – аргумент частотной передаточной функции (сдвиг фазы выходного сигнала относительно входного) Частотная передаточная функция является комплексной и в ней можно выделить действительную и мнимую части: 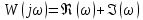 (7.1) (7.1)Общая передаточная функция разомкнутой исходной САР (5.1): 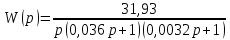 Общая передаточная функция замкнутой исходной САР (5.2): 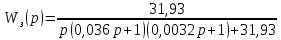 Коэффициент передачи всей САР : 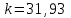 Чтобы перейти из операторной формы записи в частотную надо вместо 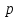 в уравнения для разомкнутой (5.3) и замкнутой систем (5.4) подставить в уравнения для разомкнутой (5.3) и замкнутой систем (5.4) подставить 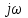 тогда частотные передаточные функции будут иметь вид: тогда частотные передаточные функции будут иметь вид: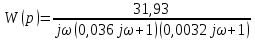 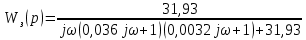 Для построения частотных характеристик системы выделить действительную (Re(w)) и мнимую (Im(w)) части из передаточной функции исходной замкнутой системы (5.4) аналогично как показано в пункте 6.2 курсовой работы. 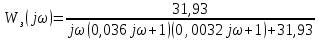 Преобразуем: 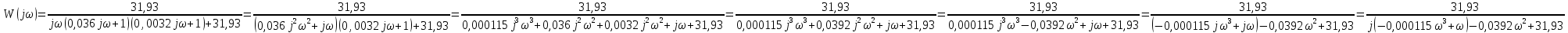 Домножим на комплексно сопряженное выражение и числитель и знаменатель (избавимся от мнимости в знаменателе): 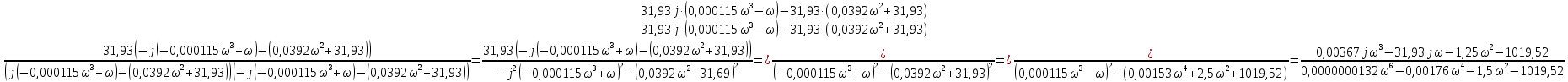 Выделим действительную и мнимую части: 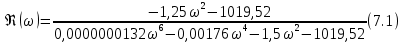 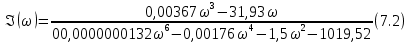 Чтобы получить наглядное представление о изменении значений мнимой (Im(w)) и действительной (Re(w)) частей из передаточной функции замкнутой исходной системы от значений частоты, подставим значения  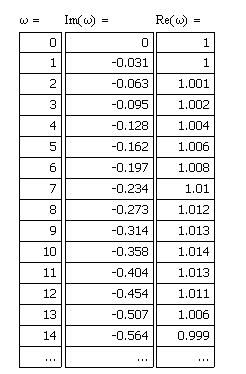 7.1. Построение АФЧХ исходной системыЧастотная передаточная функция является комплексным числом, представляющим собой вектор на комплексной плоскости, у которого длина равна модулю этого числа, а угол наклона к действительной оси – его аргументу. Тогда амплитудно-фаза-частотная характеристика будет траекторией движения этого вектора при различных значениях частоты. График АФЧХ исходной САР рисунок 7.1.1 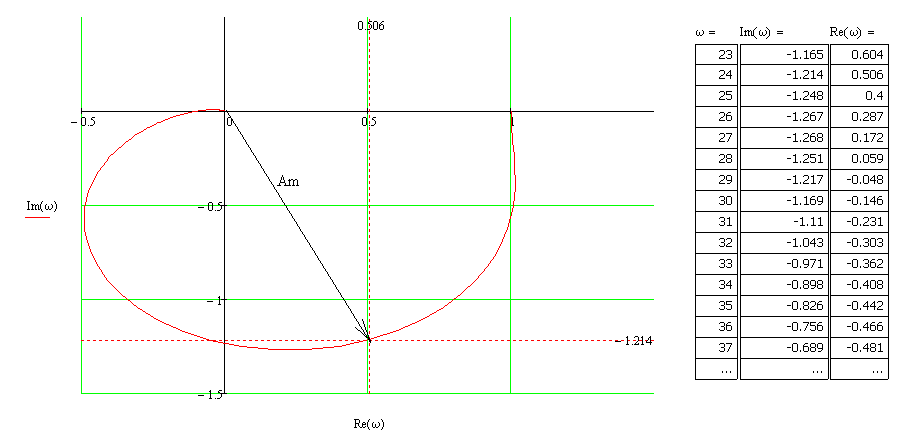 Рисунок 7.1.1 – АФЧХ исходной САР На графике показаны значения мнимой Im(ω) и действительной части Re(ω) при частоте резонанса, на которой амплитуда на АЧХ (рис.7.1.1.) максимальна. 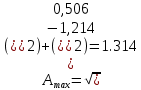 Показатель колебательности М: М= 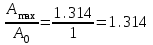 7.2 Построение АЧХ исходной системыАмплитудно-частотная характеристика (АЧХ) – это зависимость модуля комплексного числа (передаточной функции) от частоты. 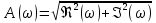 Значения мнимой (7.2) и действительной (7.1) части будут равны: 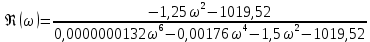 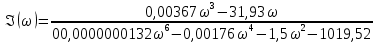 где Re(w)-действительная часть, Im(w)- мнимая часть передаточной функции. Подставляя значения от 0 до получим АЧХ замкнутой системы. 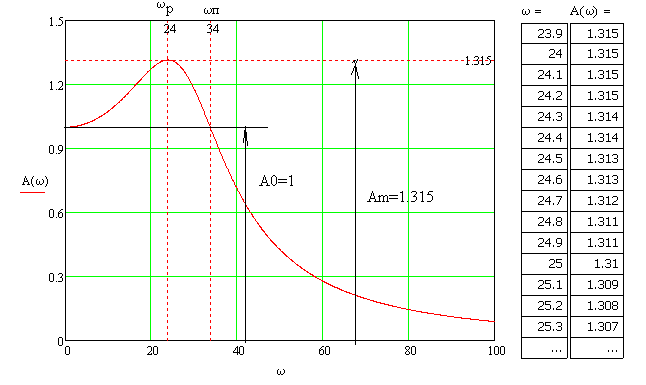 Рисунок 7.2.1 – АЧХ исходный САР Проверим качество исходной САР по показателю колебательности М: М= 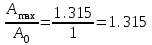 Показатель колебательности должен находиться в пределах 1,1…1,5 для качественных САР. Как видно показатель колебательности попадает в диапазон для качественных САР. По показателю колебательности М, находим перерегулирование 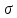 . Зная, что М=1,1 (для . Зная, что М=1,1 (для 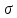 =20%), то по пропорции находим перерегулирование в системе: =20%), то по пропорции находим перерегулирование в системе: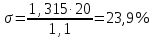 Полоса, пропуская – чем она шире, тем меньше длительность переходного процесса: 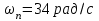 . .Время переходного процесса в первом приближении можно оценить как: 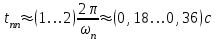 . . |
