автматика. 1. Описание принципа действия выбранной конструкции следящей системы автоматического регулирования сар 5
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
Анализ качества скорректированной САР по АФЧХ, АЧХ, ФЧХ, ВЧХ, ЛАЧХ, ЛФЧХ.Передаточная функция замкнутой скорректированной системы (8.2): 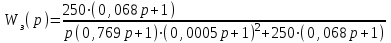 . .Комплексная передаточная функция скорректированной САР имеет следующий вид: 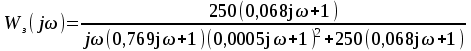 Для построения частотных характеристик системы выделить действительную (Re(w)) и мнимую (Im(w)) части из передаточной функции исходной замкнутой системы. Для того, чтобы избавиться от комплексного числа в знаменателе, необходимо и числитель и знаменатель домножить на комплексносопряжённое выражение. Пользуясь пакетом Mathcad находим действительную (Re(w)) и мнимую (Im(w)) части. 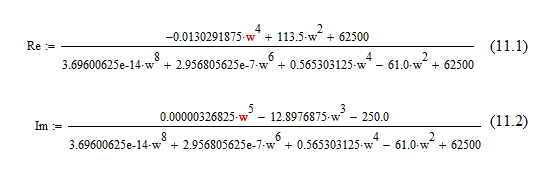 АФЧХ скорректированной САР Амплитудно-фаза-частотная характеристика будет траекторией движения этого вектора при различных значениях частоты. График АФЧХ скорректированной САР рисунок 11.1.4 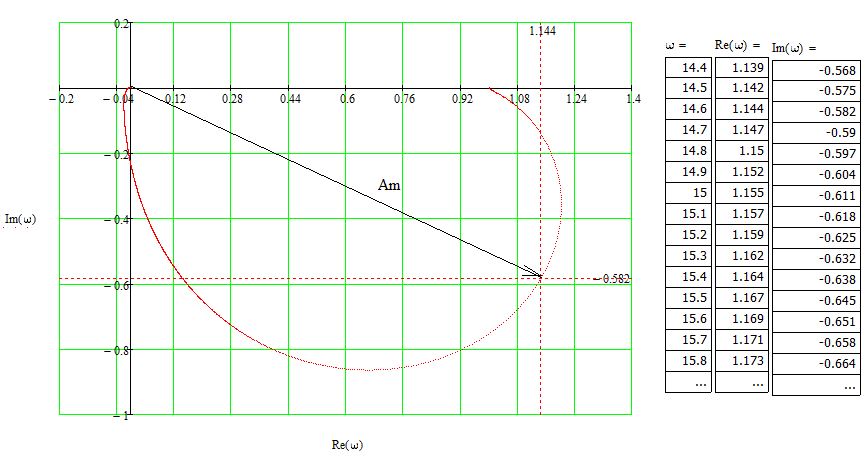 Рисунок 11.1.1 – АФЧХ скорректированной САР На графике показаны значения мнимой Im(ω) и действительной части Re(ω) при частоте резонанса, на которой амплитуда на АЧХ (рис.11.1.1.) максимальна. Найдем максимальную амплитуду: 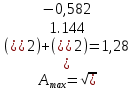 Показатель колебательности М: М= 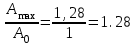 АЧХ скорректированной САР Амплитудно-частотная характеристика (АЧХ) – это зависимость модуля комплексного числа (передаточной функции) от частоты. 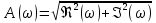 В значения мнимой (11.1) и действительной (11.2) подставляем значения от 0 до получим АЧХ замкнутой системы. 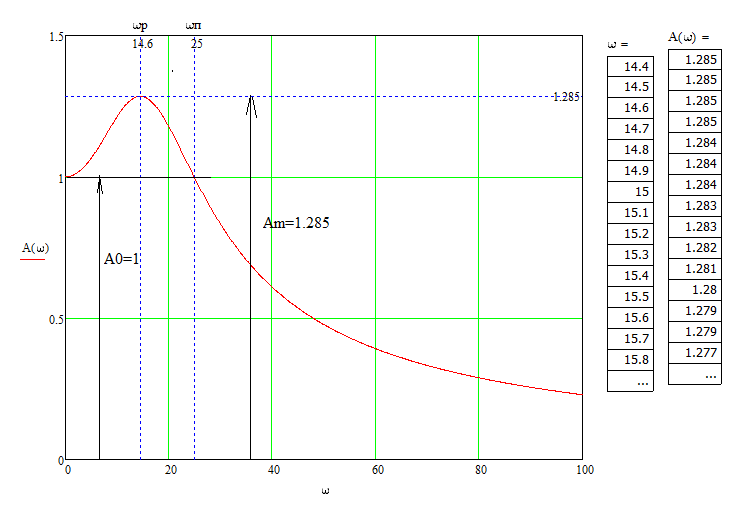 Рисунок 11.2.1 – АЧХ скорректированной САР Проверим качество скорректированной САР по показателю колебательности М: М= 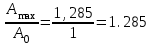 По показателю колебательности М, находим перерегулирование 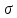 . Зная, что М=1,1 (для . Зная, что М=1,1 (для 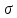 =20%), то по пропорции находим перерегулирование в системе: =20%), то по пропорции находим перерегулирование в системе: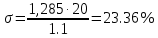 Полоса, пропуская – чем она шире, тем меньше длительность переходного процесса: 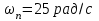 . .Время переходного процесса в первом приближении можно оценить как: 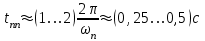 . .ФЧХ скорректированной САР Фазо-частотная характеристика – это зависимость аргумента комплексного числа (передаточной функции) от частоты. Значение фазы находятся по формуле:  Задавая значения от 0 до получим ФЧХ замкнутой системы. 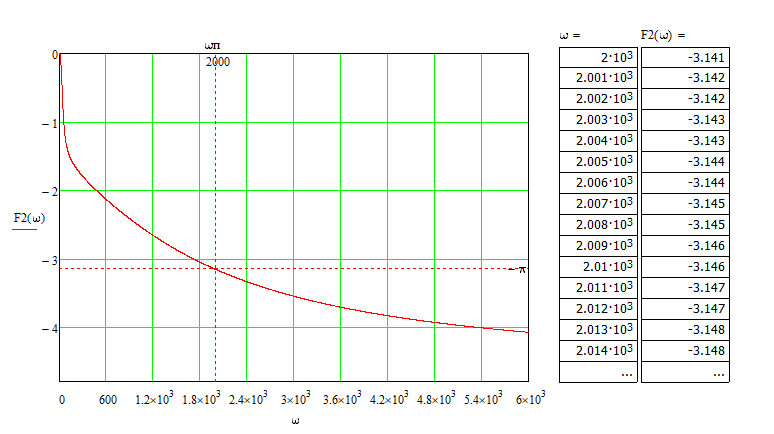 Рисунок 11.3.1- ФЧХ скорректированной САР ВЧХ скорректированной САР ВЧХ – вещественная частотная характеристика – это вещественная часть частотной передаточной функции. 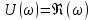 Значение вещественной части (11.1) будет равно: 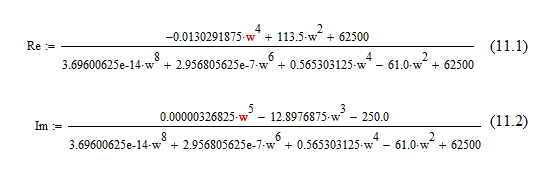 Эта характеристика соответствует уравнению: 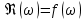 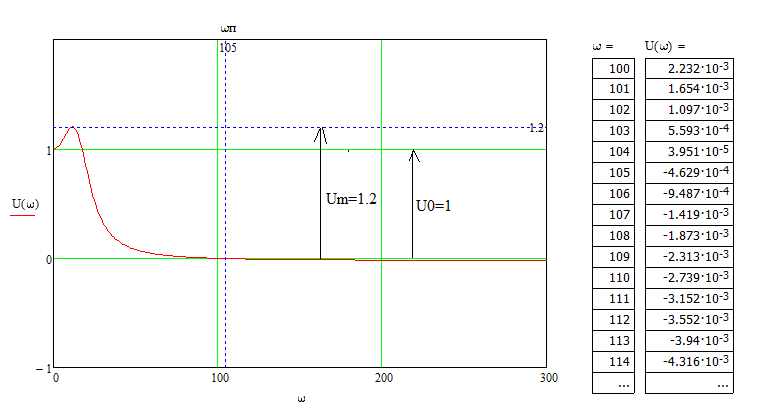 Рисунок 11.4.1 – ВЧХ скорректированной САР Определение качественных параметров с использованием ВЧХ рисунок 11.1.3: По ВЧХ можно установить следующие параметры: а) Установившееся значение переходной функции равно 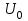 ; ;б) Перерегулирование  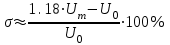 ; ;в) Время переходного процесса: 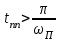 с. с.Начальная ордината ВЧХ равна установившемуся процессу переходной кривой: 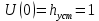 Частота 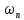 , ограничивающая интервал положительных ВЧХ: , ограничивающая интервал положительных ВЧХ: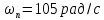 Перерегулирование в системе: 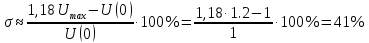 Время переходного процесса 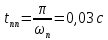 11.5. ЛАЧХ скорректированной системыЛАЧХ – логарифмическая амплитудно-частотная характеристика. Строится в логарифмическом масштабе. Начальная ордината ЛАЧХ 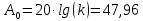 При значениях частот меньше частоты 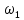 ЛАЧХ имеет наклон –20 дБ/дек. ЛАЧХ имеет наклон –20 дБ/дек.Частоты излома ЛАЧХ (сопрягающие частоты) определяются из передаточной функции (8.2): 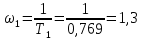 Гц Гц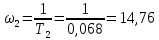 Гц Гц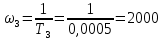 Гц Гц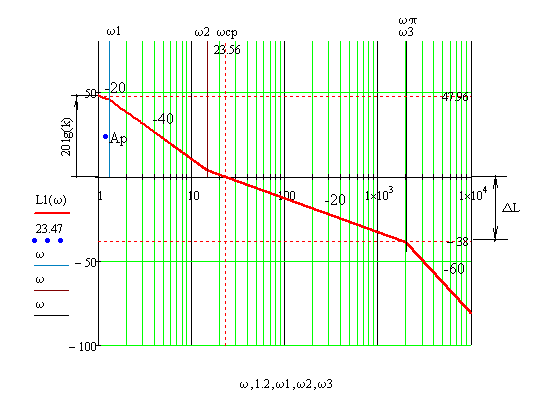 Рисунок 11.5.1 – ЛАЧХ скорректированной САР Запас устойчивости по амплитуде определим исходя из пересечения 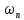 с ЛАЧХ в отрицательной области. Запас устойчивости по амплитуде равен ∆L=38 дБ/дек. с ЛАЧХ в отрицательной области. Запас устойчивости по амплитуде равен ∆L=38 дБ/дек.11.6 ЛФЧХ скорретированной САРЛФЧХ – логарифмическая фазочастотная характеристика. Определяется по формуле из передаточной функции 8,2: 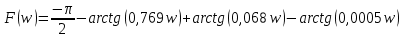 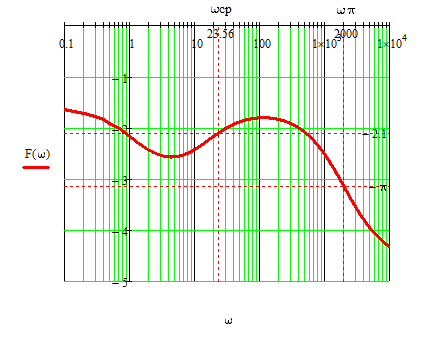 Рисунок 11.6.1- ЛФЧХ скорретированной САР Запас по фазе равен: ∆Φ= 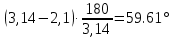 Как видно из графика, что на частоте ωп=2000, на которой ЛФЧХ пересекает прямую –π находится, ордината ЛАЧХ отрицательна, следственно САР устойчива. 12. Построение кривой переходного процесса скорректированной САР. Определение качественных параметров САРКривая переходного процесса скорректированной САР будет строится по зависимости: 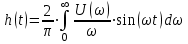 . .Кривая переходного процесса имеет вид (рисунок12.1): 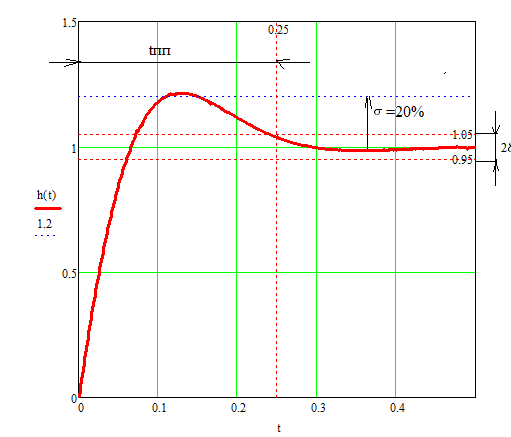 Рисунок 12.1. – Кривая переходного процесса скорректированной САР По ней можно оценить параметры качества регулирования: Время переходного процесса: 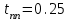 с. с.Перерегулировании: 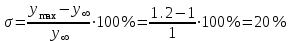 . .Число колебаний за время переходного процесса – 1. ВыводыВ результате проектирования была разработана и усовершенствована исходная САР, которая характеризуется следующими параметрами, полностью соответствующими заданию. Параметры сведены в таблицу:
Список использованной литературыСмирнова В.И. «Проектирование и расчёт автоматизированных приводов» М.,1990 Ганэ В.А., Степанов В.Л. «Расчет следящих систем» Мн.,1990 Топчеев Ю.И. «Атлас для проектирования систем автоматического регулирования» М., 1989 4. Справочник по отечественным и зарубежным полупроводниковым приборам. – 1996. –Электронное издание v 1.02. Авторы: Шульгин О.А., Щульгина И.Б., Воробьев А.Б., 645 Mb. 5. Минченя В.Т., Киселёв М.Г. Основы автоматики и автоматизация производственных процессов: Методические указания – Мн.: БНТУ, 2002. – 52 с. 6. Солодовников В. В., Плотников В.Н., Яковлев А. В. Основы теории и элементы систем автоматического регулирования. – М.: Машиностроение, 1985. – 535 с. 7. Воронов А.А., Бабаков Н.А., «Теория автоматического управления» М., 1986. 8. Клюев А.С. Автоматическое регулирование. – М.: Энергия, 1973. – 392 с. |
