автматика. 1. Описание принципа действия выбранной конструкции следящей системы автоматического регулирования сар 5
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
6.Определение устойчивости исходной САР6.1 Определение устойчивости системы по критерию ГурвицаЭтот критерий позволяет судить об устойчивости замкнутой САР (5.2) по коэффициентам ее характеристического уравнения. Замкнутая САР (5.2) будет устойчива, если положительны все коэффициенты уравнения (6.1) и положительны все главные диагональные миноры определителя Гурвица. Характеристическое уравнение (6.1) замкнутой системы (5.2) – это знаменатель ее передаточной функции (5.2). Запишем его: 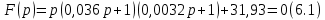 Преобразуем: 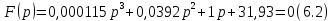 Из уравнения видно, что все коэффициенты уравнения положительны. Коэффициенты характеристического уравнения (6.3): 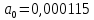 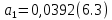 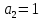 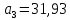 По критерию Гурвица устойчивая система должна удовлетворять следующим условиям: Коэффициенты характеристического уравнения больше нуля. 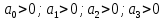 Определитель третьего порядка должен быть положительным: 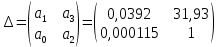 (6.4) (6.4)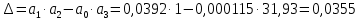 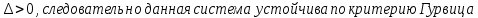 Определим критический коэффициент усиления по Гурвицу, используя условие (6.4): 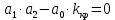 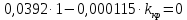 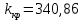 Следовательно, общий коэффициент передачи системы не должен превышать kкр. 6.2.Критерий НайквистаЗамкнутая САР будет устойчива тогда, когда разомкнутая система устойчива и если ее АФЧХ, представленная на рисунке 6.2.1, не охватывает точку с координатой (-1; j0). Эта функция имеет вид: 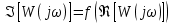 (6.5) (6.5)Найдем мнимую (Im) и действительную (Re) части разомкнутой передаточной функции (5.1), заменив оператор p на 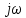 (5.3) (5.3)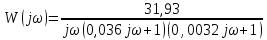 Преобразуем 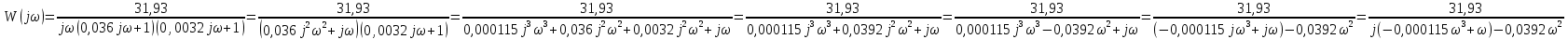 Домножим на комплексно сопряженное выражение и числитель и знаменатель (избавимся от мнимости в знаменателе): 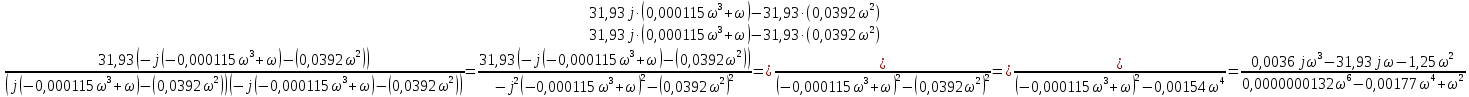 Выделим действительную и мнимую части: 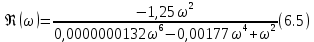 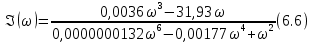 Затем, подставляя 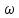 от 1 до 1000 получаем АФЧХ представленной на рисунке 6.2.1 от 1 до 1000 получаем АФЧХ представленной на рисунке 6.2.1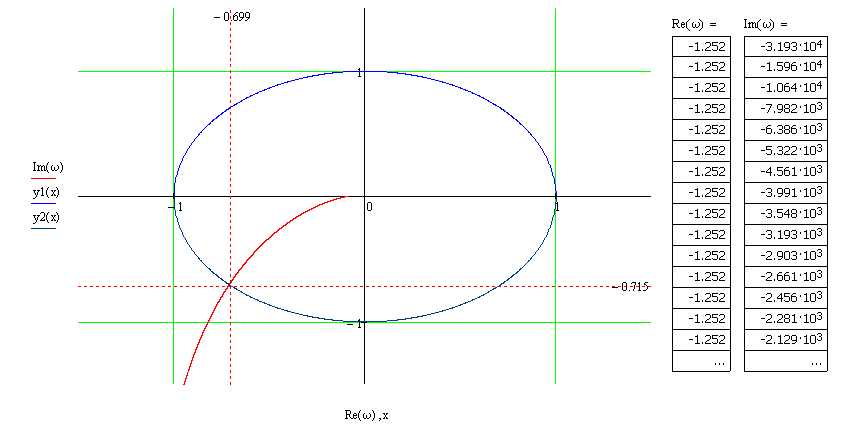 Рисунок 6.2.1 – АФЧХ разомкнутой системы Из рисунка 6.2.1 видно, что АФЧХ разомкнутой системы не охватывает точку 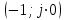 . Система устойчива. . Система устойчива.6.3.Критерий МихайловаПроверим устойчивость системы с помощью критерия Михайлова. Система будет устойчива, если функция Михайлова начинается на положительной действительной оси и огибает против часовой стрелки начало координат, проходя при этом n квадрантов (где n – порядок характеристического многочлена F(р)(6.1)). 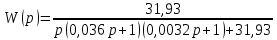 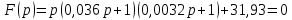 Раскроем скобки характеристического уравнения: 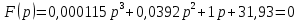 Заменим в характеристическом уравнении оператор p на 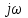 : :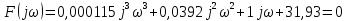 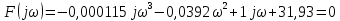 Выделим действительную и мнимую части: 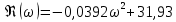 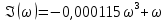 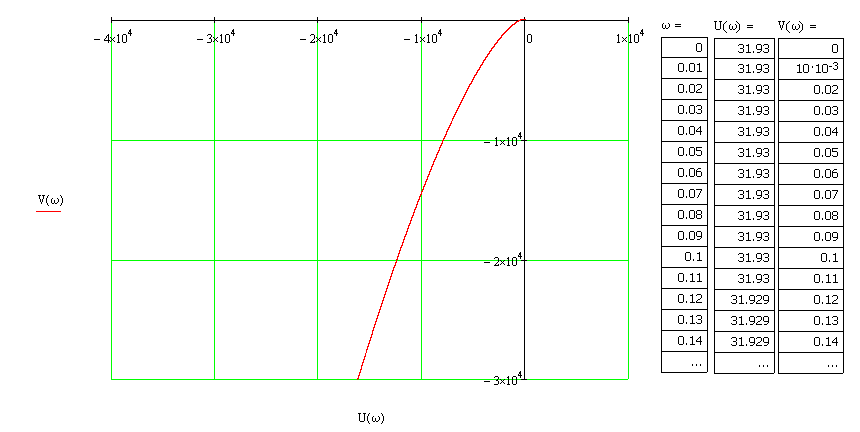 Рисунок 6.3.1 – График функции Михайлова Из графика (Рисунок 6.3.1) видно, что линейная система 3-го порядка устойчива, так как при изменении 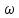 годограф Михайлова последовательно обходит 3 квадранта комплексной плоскости против часовой стрелки, начинаясь в точке на положительной вещественной полуоси и нигде не проходит через начало координат. годограф Михайлова последовательно обходит 3 квадранта комплексной плоскости против часовой стрелки, начинаясь в точке на положительной вещественной полуоси и нигде не проходит через начало координат. |
