автматика. 1. Описание принципа действия выбранной конструкции следящей системы автоматического регулирования сар 5
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
7.3. Построение ФЧХ исходной системыФазо-частотная характеристика – это зависимость аргумента комплексного числа (передаточной функции) от частоты. Значение фазы находятся по формуле:  Задавая значения от 0 до получим ФЧХ замкнутой системы. 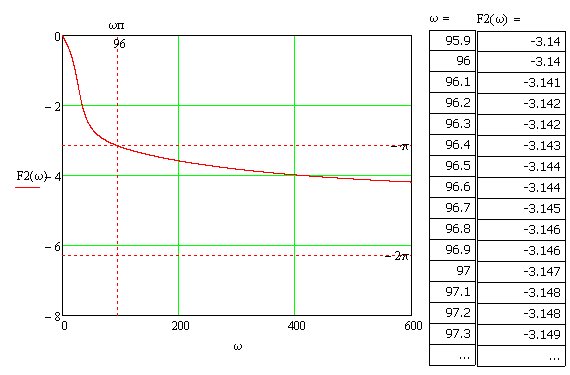 Рисунок 7.3.1- ФЧХ исходной САР Как видно из графика 7.3.1 кривая ФЧХ пересекает –π на частоте 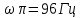 и стремится к –2π. и стремится к –2π.7.4. Построение ВЧХ исходной системыВЧХ – вещественная частотная характеристика – это вещественная часть частотной передаточной функции. 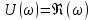 Значение вещественной части (7.1) будет равно: 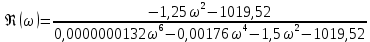 Эта характеристика соответствует уравнению: 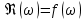 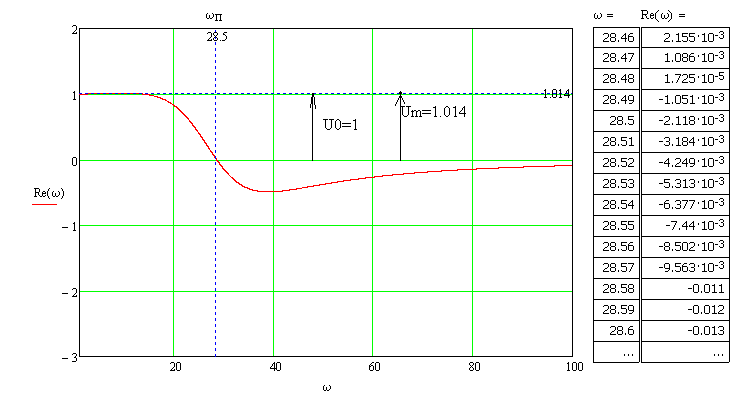 Рисунок 7.4.1 – ВЧХ исходной САР Определение качественных параметров с использованием ВЧХ рисунок 7.4.1: По ВЧХ можно установить следующие параметры: а) Установившееся значение переходной функции равно 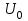 ; ;б) Перерегулирование  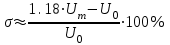 ; ;в) Время переходного процесса: 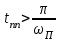 с. с.Начальная ордината ВЧХ равна установившемуся процессу переходной кривой: 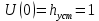 Частота 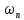 , ограничивающая интервал положительных ВЧХ: , ограничивающая интервал положительных ВЧХ: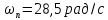 Перерегулирование в системе: 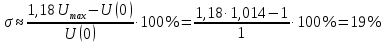 Время переходного процесса 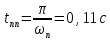 7.5. Построение ЛАЧХ исходной системыЛАЧХ – логарифмическая амплитудно-частотная характеристика. Строится в логарифмическом масштабе. Начальная ордината ЛАЧХ 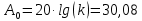 При значениях частот меньше частоты 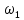 ЛАЧХ имеет наклон –20 дБ/дек. ЛАЧХ имеет наклон –20 дБ/дек.Частоты излома ЛАЧХ (сопрягающие частоты) определяются из передаточной функции (5.4): 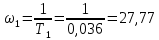 Гц Гц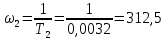 Гц ГцПри частотах от 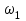 до до 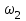 ЛАЧХ имеет наклон -40 дБ/дек, при частотах от ЛАЧХ имеет наклон -40 дБ/дек, при частотах от 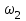 и частотах больше ЛАЧХ имеет наклон -60 дБ/дек. При частоте равной единице ЛАЧХ проходит через точку с ординатой и частотах больше ЛАЧХ имеет наклон -60 дБ/дек. При частоте равной единице ЛАЧХ проходит через точку с ординатой 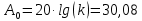 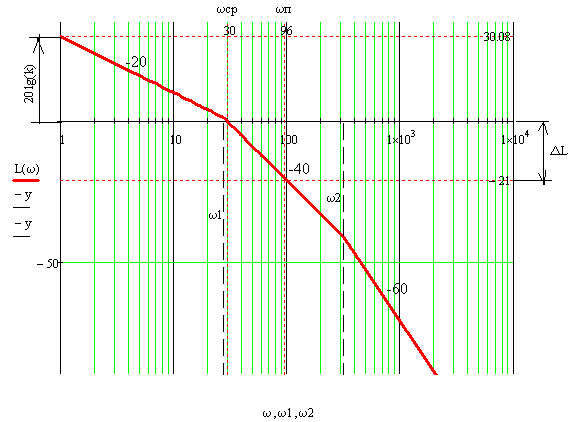 Рисунок 7.5.1 – ЛАЧХ исходной САР Запас устойчивости по амплитуде определим исходя из пересечения 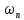 с ЛАЧХ в отрицательной области. Запас устойчивости по амплитуде равен ∆L=21 дБ/дек; с ЛАЧХ в отрицательной области. Запас устойчивости по амплитуде равен ∆L=21 дБ/дек;7.6. Построение ЛФЧХ разомкнутой системыЛФЧХ – логарифмическая фазочастотная характеристика. Определяется по формуле из передаточной функции 5.4: 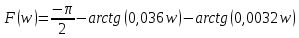 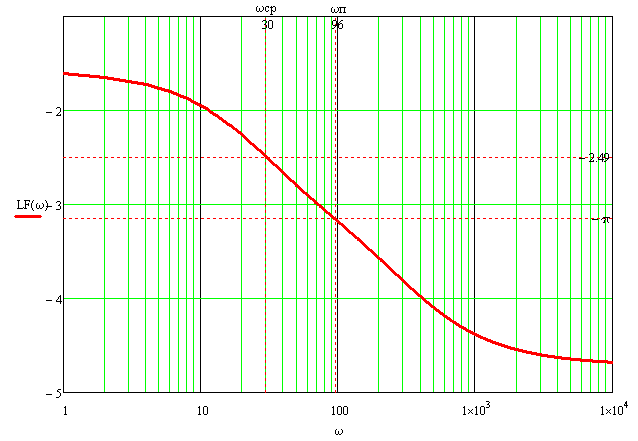 Рисунок 7.6.1 – ЛФЧХ исходной САР Запас по фазе равен: ∆Φ= 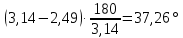 |
