1. Оптикой
 Скачать 4.65 Mb. Скачать 4.65 Mb.
|
|
17 Уравнение эйконала. Запишем волновое уравнение для световой волны в среде с коэффициентом преломления n=c/v: 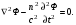 (5.1) (5.1)В общем случае для монохроматической волны справедливо: 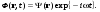 (5.2) (5.2)Подставляя (5.2) в (5.1) находим уравнение для амплитуды Y(r), зависящей только от координаты: 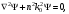 (5.3) (5.3)где k0=w/c – волновое число в вакууме. Волновое число в среде k=nk0. Воспользуемся соотношением (для других координат будет аналогично): 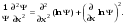 (5.4) (5.4)Тогда (5.3) после деления на Y преобразуется к виду: 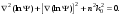 (5.5) (5.5)Решение этого уравнения ищем в виде: 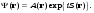 (5.6) (5.6)Вещественная скалярная функция S(r) называется эйконалом(от греческого eikon – изображение). Подставляя (5.6) в (5.5), получаем: 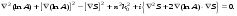 (5.7) (5.7)Приравнивая нулю вещественную и мнимую части, получим два уравнения для определения А(r) и S(r): 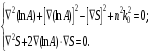 (5.8) (5.8)Для оптического диапазона длина волны много меньше расстояния L, на которых амплитуда волны существенно меняется (порядка размера оптических элементов). Поэтому первыми двумя слагаемыми в первом уравнении (5.8) можно пренебречь (их сумма имеет порядок 1/L2). Тогда это уравнение в оптическом диапазоне принимает вид: 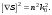 (5.9) (5.9)Это уравнение называется уравнением эйконала. Градиент от функции S(r) направлен по нормали к поверхности S=const. Поэтому эйконал S описывает поверхности постоянной фазы волны, а ÑS приводит к понятию луча, т.е. к представлению о движении световой энергии в данной точке в определенном направлении. Лучом называется линия, касательная к которой совпадает в каждой точке с вектором ÑS. Распространение света рассматривается как движение световой энергии по лучам. Плоскость, перпендикулярная лучам света (где S = const), называется волновым фронтом. Анализ распространения света в лучевом приближении составляет предмет геометрической оптики. Этот подход оправдан всегда, когда 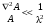 . (5.10) . (5.10)Физически этот член описывает искривление материальными объектами световых лучей, т.е. дифракцию света. Исходя из этого, можно сказать, что в геометрической оптике не учитываются дифракционные эффекты (см. гл.7). 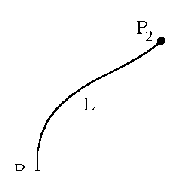 Принцип Ферма. В однородной среде S=k×r (k=const) и лучи являются прямыми параллельными линиями, а фронт волны – плоскостью, перпендикулярной лучам. Принцип Ферма. В однородной среде S=k×r (k=const) и лучи являются прямыми параллельными линиями, а фронт волны – плоскостью, перпендикулярной лучам. Для неоднородной среды лучи имеют более сложную конфигурацию. Пусть точки P1и P2 соединяются лучом L (рис.5.1). Вычислим изменение фазы вдоль луча. Для каждой его точки имеем: 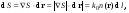 (5.11) (5.11)где dr направлен по лучу и совпадает с ÑS, dl – элемент длины пути. Для изменения фазы находим: 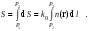 (5.12) (5.12)Интегрирование идет вдоль луча. Интеграл в (5.12) называется оптической длиной пути. Из (5.12) следует, что оптические длины путей вдоль различных лучей между точками волнового фронта в два момента времени одинаковы. Для любой другой кривой, соединяющей точки P1и P2 , оптическая длина пути оказывается больше, чем для реального луча. Принцип Ферма (Fermat Pierre, 1601 – 1675) утверждает, что интеграл в (5.12) вдоль луча имеет стационарное значение, т.е. первая вариация dS относительно соседних путей интегрирования равна нулю. Или то же самое в другой формулировке: реальный луч отличается от остальных кривых, соединяющих две заданные точки, тем, что соответствующая ему оптическая длина имеет стационарное значение, т.е. малое изменение траектории не приводит к изменению оптической длины. К принципу Ферма можно подойти и с другой стороны. Учтем что dt=dl / v – время прохождения пути dl со скоростью v, а n(r) = c / v(r). Тогда 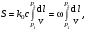 (5.13) (5.13)где интеграл здесь дает время, затрачиваемое на прохождение пути от P1и P2. С этой точки зрения принцип Ферма звучит так: лучом, соединяющим две точки, является тот путь, который делает стационарным время, затрачиваемое светом на его прохождение. Формулировка о стационарности времени прохождения пути между двумя точками, с одной стороны, утверждает экстремальный характер этого времени, а с другой стороны, не исключает наличия нескольких путей с одинаковым временем прохождения. Например, в геометрической оптике все лучи от точки предмета идут по различным путям и встречаются в точке изображения. Но все они затрачивают одно и то же время на прохождение своего пути. Другими словами, оптические длины всех путей, соединяющих точку предмета с точкой изображения, одинаковы (принцип таутохронизма). 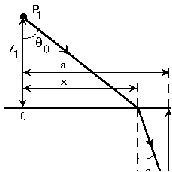 18 Вывод закона преломления из принципа Ферма. Пусть требуется соединить лучом две точки P1и P2 , находящиеся в однородных средах с коэффициентами преломления n1и n2, разделенных плоской границей (рис. 5.2). В каждой однородной среде луч – прямая линия. Из геометрии рисунка получаем для полного времени распространения света между точками P1и P2: 18 Вывод закона преломления из принципа Ферма. Пусть требуется соединить лучом две точки P1и P2 , находящиеся в однородных средах с коэффициентами преломления n1и n2, разделенных плоской границей (рис. 5.2). В каждой однородной среде луч – прямая линия. Из геометрии рисунка получаем для полного времени распространения света между точками P1и P2: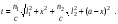 (5.14) (5.14)Условие стационарности 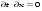 принимает вид: принимает вид: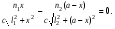 (5.15) (5.15)Учитывая, что 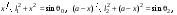 получаем соотношение , полностью совпадающее с законом Снеллиуса: получаем соотношение , полностью совпадающее с законом Снеллиуса: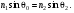 (5.16) (5.16)Распространение луча в среде с переменным коэффициентом преломления. Пусть свет распространяется в среде с аксиально-симметричным изменением коэффициента преломления. Луч распространяется вдоль положительного направления этой оси Z в параксиальном приближении. Расстояние от оси – r. Из закона Снеллиуса для бесконечно тонкого слоя Dr имеем: 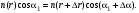 (5.17) (5.17)Разложим n(r + Dr) в ряд Тейлора и ограничимся линейным по Dr членом: 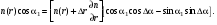 (5.18) (5.18)В параксиальном приближении sinDa » Da; cosDa » 1. Тогда с учетом линейного приближения получаем: 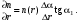 (5.19) (5.19)Т.к. tga1 = Dr / Dz , то в параксиальном приближении: 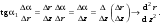 (5.20) (5.20)С учетом (5.20) из (5.19) находим уравнение распространения луча: 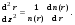 (5.21) (5.21)Например для диэлектрического волоконного световода n(r)=n0(1– ar2/2)и ar2/2«1(a>0). Тогда уравнение (5.21) принимает вид: d2r/dz2 = – ar. Общее решение этого уравнения гармонических колебаний в пространстве хорошо известно. Это значит, что луч внутри такого световода имеет синусоидальную траекторию. 19Прохождение лучей в центрированных оптических системах. Рассмотрим прохождение лучей через сферическую линзу, не накладывая ограничений на ее толщину (рис.5.3). Обозначения видны из рисунка. Ось Z совпадает с осью линзы. Главной оптической осью линзы называется прямая, проходящая через центры кривизны ее поверхности (в данном построении это ось Z). Свет распространяется вдоль положительного направления оси Z. Луч света лежит в плоскости XZ. r1 и r2 – радиусы кривизны 1-й и 2-й сферических поверхностей линзы (r2 на рис.5.3 не показан, чтобы не загромождать рисунок). Весь расчет проводится в параксиальном приближении: 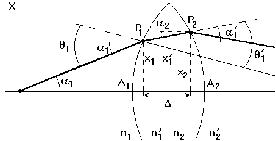 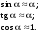 (5.22) (5.22)Преломление на первой сферической поверхности. В точке P1 закон Снеллиуса в параксиальном приближении имеет вид: 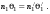 (5.23) (5.23)Используя геометрические соотношения между углами:  (5.24) (5.24)а в параксиальном приближении 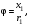 (5.25) (5.25) из (5.23) получаем: 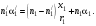 (5.26) (5.26)Кроме этого учтем соотношение 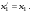 (5.27) (5.27)Система уравнений (5.26) и (5.27) позволяют, задав координаты падающего на первую поверхность линзы луча (n1a1 ; x1), найти координаты (n1/a1/ ; x1/) преломленного в линзе луча. Полученную систему удобно записать в матричном виде: 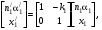 (5.28) (5.28)где величина k1=(n1/–n1)/r1 называется преломляющей силой первой поверхности, а матрица 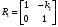 (5.29) (5.29)называется преломляющей матрицей первой поверхности. Распространение луча внутри линзы. Преломленный луч в параксиальном приближении, пройдя внутри линзы, падает на её вторую поверхность на расстоянии x2 от оси: 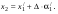 (5.30) (5.30)Отметим, что величина D в параксиальном приближении практически равна толщине линзы А1А2 . С учетом, что 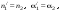 получаем в матричном виде: получаем в матричном виде: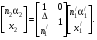 (5.31) (5.31)Матрица 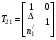 (5.32) (5.32)описывает распространение луча от первой поверхности линзы ко второй и называется передаточной матрицей. Преломление луча на второй сферической поверхности рассматривается точно так же, как и на первой поверхности. Величина k2=(n2/ –n2)/r2 называется преломляющей силой второй поверхности, а матрица R2– преломляющей матрицей второй поверхности: 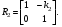 (5.33) (5.33)Знаки всех величин в приведенных выражениях необходимо брать с учётом правилазнаков: если встречаемая лучом преломляющая поверхность выпуклая, то её радиус кривизны надо брать с положительным знаком, а если вогнутая – с отрицательным; углы a, отсчитываемые от оси Z против часовой стрелки, положительны, а по часовой стрелке – отрицательны; расстояния, отсчитываемые по Z (по рис. 5.3 – слева направо), положительны, а против Z (справа налево) – отрицательны; расстояния от оси Z, отсчитываемые вверх, положительны, вниз – отрицательны. Распространение луча через оптическую систему. Используя (5.29), (5.31), (5.33), получаем связь между характеристиками на выходе линзы и входе в неё: 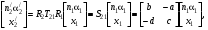 (5.34) (5.34)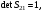 (5.35) (5.35)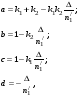 (5.36) (5.36)где a, b, c, d называются постоянными Гаусса. Независимыми являются только три из четырех постоянных Гаусса. Матрица S21 полностью описывает рассмотренную оптическую систему. Преобразование луча от плоскости предмета к плоскости изображения. Пусть из точки некоторой плоскости (плоскости предмета), расположенной на расстоянии l слева от точки А1 выходит луч с координатами (n1a1, x) и падает на рассматриваемую линзу. В некоторой плоскости, расположенной справа от точки А2 на расстоянии l/ луч характеризуется координатами (n2/a2/, x/). Между этими парами координат по приведенным выше правилам получаем соотношение: 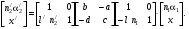 (5.37) (5.37)(Знак l уже учтён)Перемножая матрицы в (5.37), имеем: 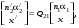 (5.38) (5.38)Матрица Q21 называется матрицей преобразования предмета к изображению: 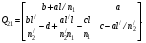 (5.39) (5.39)Обозначим 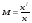 (5.40) (5.40)– увеличение оптической системы. Введем понятие изображения. Под изображением понимается такое отображение плоскости предмета на плоскость, называемую плоскостью изображения, когда все лучи, исходящие от точки предмета, сходятся после преломления в оптической системе в одной точке плоскости изображения и все точки отображаются с одинаковым увеличением. Исходя из этого определения в точке изображения увеличение М не должно зависеть от угла a1. Поэтому соответствующий член в матрице Q21 обращается в нуль: 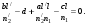 (5.41) (5.41)Из определения увеличения и выражения (5.40) имеем: 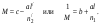 (5.42) (5.42)Тогда матрица преобразования от предмета к изображению принимает вид: 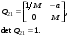 (5.43) (5.43)20 Кардинальные элементы оптической системы. Плоскости H и H/, увеличение для точек которых М = 1, называются главными плоскостями, а их пересечения с осью системы (ось Z) – главными точками системы. Найдём из (5.42) их положение: 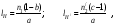 (5.44) (5.44)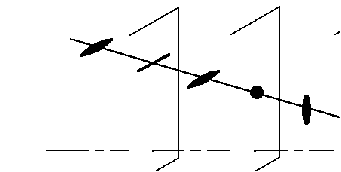 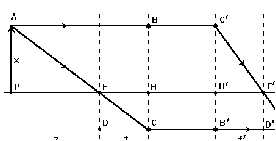 где lH – отсчёт положения плоскости H относительно точки А1; lH/ – отсчёт положения плоскости H относительно точки А2 . Точка на оси системы, в которой сходятся лучи, падающие на оптическую систему параллельно оптической оси (т.е. точка с увеличением M = 0) и точка, выйдя из которой лучи после прохождения оптической системы становятся параллельными оптической оси (т.е. с увеличением M = ¥), называются фокусами оптической системы. Плоскости, проходящие через фокусы перпендикулярно оптической оси, называются фокальными. Найдём из (5.42) их положение: где lH – отсчёт положения плоскости H относительно точки А1; lH/ – отсчёт положения плоскости H относительно точки А2 . Точка на оси системы, в которой сходятся лучи, падающие на оптическую систему параллельно оптической оси (т.е. точка с увеличением M = 0) и точка, выйдя из которой лучи после прохождения оптической системы становятся параллельными оптической оси (т.е. с увеличением M = ¥), называются фокусами оптической системы. Плоскости, проходящие через фокусы перпендикулярно оптической оси, называются фокальными. Найдём из (5.42) их положение: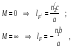 (5.45) (5.45)где lF– отсчёт положения переднего фокуса относительно точки А1 , lF/ – отсчёт положения заднего фокуса относительно точки А2 Расстояние f между передним фокусом и передней главной точкой называется передним фокусным расстоянием; расстояние f/между задним фокусом и задней главной точкой называется задним фокусным расстоянием: 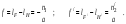 (5.46) (5.46)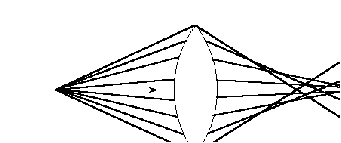 Главные и фокальные плоскости называются кардинальными элементами оптической системы. Их положение позволяет полностью описать преломление лучей в оптической системе и построить изображение заданного предмета (рис). Физический смысл постоянных Гаусса. Пусть линза располагается в воздухе: n1 = n2/ = 1. Тогда из (5.46) следует: Главные и фокальные плоскости называются кардинальными элементами оптической системы. Их положение позволяет полностью описать преломление лучей в оптической системе и построить изображение заданного предмета (рис). Физический смысл постоянных Гаусса. Пусть линза располагается в воздухе: n1 = n2/ = 1. Тогда из (5.46) следует: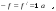 (5.47) (5.47)т.е. a является величиной, обратной фокусному расстоянию. Из (5.45) и (5.47) имеем: 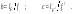 (5.48) (5.48)Коэффициенты b и c характеризуют взаимное расположение главных и фокальных плоскостей. Уравнение линзы. Из подобия треугольников CDF, ABC, FPA (рис.5.4) следует: 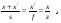 (5.49) (5.49)а из подобия треугольников A/D/F/, F/H/C/, A/B/C/ следует: 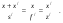 (5.50) (5.50)Из этих соотношений имеем: 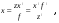 (5.51) (5.51)а отсюда получаем уравнение линзы в форме Ньютона: 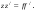 (5.52) (5.52)Из этих же уравнений можно получить уравнение линзы в форме Гаусса: 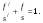 (5.53) (5.53)Увеличение линзы определяется из формулы:  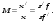 (5.54) (5.54) |
