1. Оптикой
 Скачать 4.65 Mb. Скачать 4.65 Mb.
|
1/w , а регистрируются лишь усредненные по многим периодам колебаний значения. Усреднение квадратов гармонических функций. Получим аналогичные выражения для квадратов гармонических функций:Складывая почленно (2.55) и (2.56) и обозначив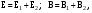 (2.57) получаем: (2.57) получаем: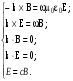 (2.58) (2.58)Две плоские монохром. бегущие ЭМВ с одинаковой частотой, распростр. в одном и том же напр., в результате сложения дают плоскую монохроматическую ЭМВ той же частоты, распр. в том же направлении. Биения. Рассмотрим случай, когда w1 ¹ w2 , E1 || E2 : 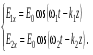 (2.59) (2.59)В соответствии с принципом суперпозиции имеем: 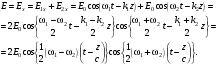 (2.60) (2.60)Мы получили незатухающую бегущую в сторону +Z немонохроматическую волну. Т.к. в оптическом диапазоне обычно | w1 – w2 | << w1 + w2 , то сомножитель 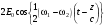 в (2.60) является медленно меняющейся амплитудой ЭМВ с частотой (w1 + w2) / 2 (см. рис.2.3). Гармонические колебания с медленно изменяющейся амплитудой называются биениями. Понятие «медленно изменяющаяся амплитуда» определяется относительно основного гармонического колебания: амплитуда мало меняется в течение многих периодов основного гармонического колебания. Частота W = |w1 – w2| называется частотой биений. Стоячие волны. Рассм. суперпозицию двух монохроматических волн с w1 = w2 = w , E10= E20 = E0 , E1 || E2 и распространяющихся навстречу друг другу: в (2.60) является медленно меняющейся амплитудой ЭМВ с частотой (w1 + w2) / 2 (см. рис.2.3). Гармонические колебания с медленно изменяющейся амплитудой называются биениями. Понятие «медленно изменяющаяся амплитуда» определяется относительно основного гармонического колебания: амплитуда мало меняется в течение многих периодов основного гармонического колебания. Частота W = |w1 – w2| называется частотой биений. Стоячие волны. Рассм. суперпозицию двух монохроматических волн с w1 = w2 = w , E10= E20 = E0 , E1 || E2 и распространяющихся навстречу друг другу: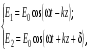 (2.61) (2.61)где d – разность фаз. Тогда 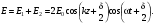 (2.62) (2.62)Сомножитель 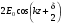 с точностью до знака можно рассматривать как амплитуду колебаний напряженности поля в заданной точке z . Она изменяется от точки к точке по гармоническому закону. Напряженность во всех точках изменяется с одинаковой частотой в одной фазе. Такая волна называется стоячей. В точках оси Z, где с точностью до знака можно рассматривать как амплитуду колебаний напряженности поля в заданной точке z . Она изменяется от точки к точке по гармоническому закону. Напряженность во всех точках изменяется с одинаковой частотой в одной фазе. Такая волна называется стоячей. В точках оси Z, где 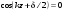 поле E = 0 (такие точки называются узлами). В точках оси Z, где поле E = 0 (такие точки называются узлами). В точках оси Z, где 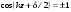 поле E – максимально (такие точки называются пучностями). Расстояние между узлами (или пучностями) равняется половине длины бегущей волны – l/2. Кроме того, колебания напряженности во всех точках стоячей волны в некоторый момент времени находятся в одной и той же фазе (например, E = 0 во всех z при поле E – максимально (такие точки называются пучностями). Расстояние между узлами (или пучностями) равняется половине длины бегущей волны – l/2. Кроме того, колебания напряженности во всех точках стоячей волны в некоторый момент времени находятся в одной и той же фазе (например, E = 0 во всех z при 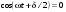 ), тогда как колебания напряженности электрического поля в различных точках бегущей волны не совпадают по фазе. ), тогда как колебания напряженности электрического поля в различных точках бегущей волны не совпадают по фазе.Магнитная индукция в данном случае получается из суперпозиции магнитных индукций волн: 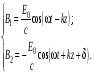 (2.63) (2.63)Суммарное поле отыщется в виде: 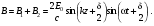 (2.64) (2.64)Видно, что вектор B также образует стоячую волну, узлы которой совпадают с пучностями стоячей волны E (рис.2.4).По времени колебаний электрического и магнитного полей стоячей ЭМВ отличаются по фазе на четверть периода колебаний. Это означает, что если E достигает максимума, то B = 0, если же E растет, то B уменьшается. Преобразование энергии в стоячей волне. Т.к. 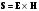 , то поток энергии отсутствует в точках, где E = 0 или B = 0 (H = 0). Поток энергии через узлы и пучности в такой волне отсутствует. Поэтому с течением времени энергия движется между соседними узлами и пучностями, превращаясь из энергии магнитного поля в энергию электрического поля и наоборот, а пользуясь формулой для объемной плотности энергии электромагнитного поля , то поток энергии отсутствует в точках, где E = 0 или B = 0 (H = 0). Поток энергии через узлы и пучности в такой волне отсутствует. Поэтому с течением времени энергия движется между соседними узлами и пучностями, превращаясь из энергии магнитного поля в энергию электрического поля и наоборот, а пользуясь формулой для объемной плотности энергии электромагнитного поля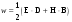 (2.65) (2.65)можно сказать, что энергия стоячей волны, заключенная между соседними узлами и пучностями, остается постоянной с течением времени. 6 Поляризация электромагнитных волн. Если для продольных волн (например, звуковых) все направления, перпендикулярные направлению распространения волн, равноправны, то для электромагнитных, т.е. поперечных волн они не равноправны. Поляризация света – это физическая характеристика оптического излучения, описывающая поперечную анизотропию световых волн, т.е. неэквивалентность различных направлений в плоскости, перпендикулярной направлению распространения волны. Представление о поляризации света как его особом физическом свойстве впервые ввел И. Ньютон (Newton Isaak, 1643–1727) в 1704 г. Сам термин «поляризация» принадлежит французскому инженеру и физику Э. Малюсу (Malus Etienne, 1775–1812). Световые волны, у которых направления колебаний векторов электрического E и магнитного H полей сохраняются неизменными в пространстве или изменяются по определенному закону, называются поляризованными. Если вектор E световой волны колеблется лишь в одной неизменной в пространстве плоскости, то такая волна называется линейноилиплоскополяризованной. При линейной поляризации плоскость, содержащая волновой вектор k и вектор E, называется плоскостью поляризации волны. Если же колебания вектора E совершаются так, что его конец описывает окружность в плоскости, перпендикулярной направлению распространения волны k, то такая волна называется поляризованнойпокругу, еслиэллипс, то эллиптическиполяризованной. Световая волна, в которой различные направления вектора E в поперечной к направлению распространения волны плоскости равновероятны, называется естественной(естественнополяризованнойилинеполяризованной). Суперпозиция двух линейно поляризованных волн.Рассмотрим суперпозицию двух линейно поляризованных волн с одинаковыми частотами w, амплитудами электрических полей E1 и E2, распространяющихся в одном направлении (вдоль оси Z декартовой системы координат) со сдвигом фаз d. Пусть вектор E1 колеблется в плоскости XZ, а вектор E2 – в плоскости YZ: 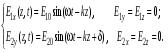 (2.66) (2.66)Найдем состояние поляризации суммарной волны, определяемой суперпозицией полей E ={Ex; Ey; Ez}= E1+E2, складывая покоординатно поля (2.66). Второе уравнение в (2.66) перепишем в виде: 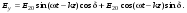 (2.67) (2.67)Исключая в (2.67) с помощью (2.66) 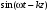 и и 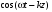 , получаем: , получаем: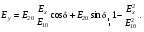 (2.68) (2.68)После перегруппировки получаем окончательно уравнение, описывающее состояние поляризации суммарного поля в общем виде: 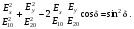 (2.69) (2.69)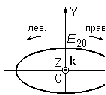 7. Волна с круговой и элептической поляриз.Рассмотрим основные случаи состояния поляризации. Если 7. Волна с круговой и элептической поляриз.Рассмотрим основные случаи состояния поляризации. Если 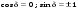 , то уравнение (2.69) принимает вид: , то уравнение (2.69) принимает вид: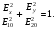 (2.70) (2.70)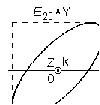 При При 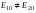 это выражение является уравнением эллипса с центром в начале системы координат и осями, направленными вдоль осей X и Y (рис.2.5). Поляризация при этом называется эллиптической. Если при наблюдении навстречу волне вращение вектора E в фиксированной плоскости (перпендикулярной волновому вектору) происходит по часовой стрелке, то такая волна называется правойэллиптически поляризованной волной, если против часовой стрелки – левой эллиптически поляризованной волной. это выражение является уравнением эллипса с центром в начале системы координат и осями, направленными вдоль осей X и Y (рис.2.5). Поляризация при этом называется эллиптической. Если при наблюдении навстречу волне вращение вектора E в фиксированной плоскости (перпендикулярной волновому вектору) происходит по часовой стрелке, то такая волна называется правойэллиптически поляризованной волной, если против часовой стрелки – левой эллиптически поляризованной волной. Если 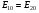 , то эллипс вырождается в окружность. Такая поляризация называется круговойили циркулярной. Понятия правой и левой круговой поляризации применимы здесь аналогично определенным выше для эллиптической поляризации. , то эллипс вырождается в окружность. Такая поляризация называется круговойили циркулярной. Понятия правой и левой круговой поляризации применимы здесь аналогично определенным выше для эллиптической поляризации.При 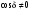 (общий случай выражения (2.69)) поляризация является также эллиптической, главные оси эллипса не совпадают с осями координат (рис.2.6). Ориентация эллипса зависит от сдвига фаз d. При этом эллиптичность поляризации остается и при (общий случай выражения (2.69)) поляризация является также эллиптической, главные оси эллипса не совпадают с осями координат (рис.2.6). Ориентация эллипса зависит от сдвига фаз d. При этом эллиптичность поляризации остается и при 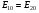 . .При 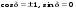 уравнение (2.69) описывает прямые: уравнение (2.69) описывает прямые: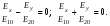 (2.71) (2.71)Конец суммарного вектора электрического 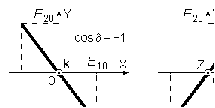 поля движется вдоль соответствующего отрезка прямой (2.71) (рис.2.7). Получаемая линейно поляризованнаяволнаявляется предельным случаем эллиптически поляризованной волны. поля движется вдоль соответствующего отрезка прямой (2.71) (рис.2.7). Получаемая линейно поляризованнаяволнаявляется предельным случаем эллиптически поляризованной волны.Видно, что световая волна с любой поляризацией может быть представлена в виде суперпозиции двух линейно поляризованных во взаимно-перпендикулярных плоскостях волн. Поэтому можно сказать, что электромагнитные волны обладают двумя независимыми состояниями поляризации. Рассмотрим противоположный случай – суперпозицию волн с левой и правой круговыми поляризациями. Пусть при некоторой фиксированной координате z заданы компоненты их полей E1 (левая) и E2 (правая): 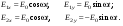 (2.72) (2.72)В результате их суперпозиции получается линейно поляризованная волна с 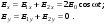 (2.72) (2.72)Если между двумя круговыми волнами в (2.71) есть сдвиг фаз, то результирующий вектор линейно поляризованной волны будет колебаться в плоскости, расположенной под некоторым углом к оси X. Усреднения. Если в физических теориях обычно пользуются мгновенными значениями величин, то в физическом эксперименте измеряют средние значения величин по некоторому объему и промежутку времени: 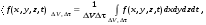 (2.73) (2.73)где DV и Dt – соответственно объем и интервал времени усреднения. Результат усреднения зависит от размеров области усреднения. Масштабы изменения f, меньшие области усреднения, не фиксируются в усредненных величинах. Если в области усреднения DV в любой момент промежутка времени Dt усреднения величина f изменяется незначительно и этим изменением можно пренебречь, то все операции усреднения в этом случае сводятся к усреднению по времени: 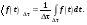 (2.74) (2.74)Отметим, что из определения операции усреднения следует, что эта операция является линейной. Усреднение гармонических функций. Воспользуемся известными формулами для определенных интегралов. Так как 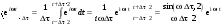 (2.75) (2.75)и 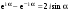 , то , то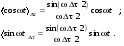 (2.76) (2.76)Результатом усреднения гармонической функции является гармоническая функция с той же частотой, но с амплитудой, умноженной на 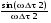 .Амплитуда усредненной гармонической функции быстро убывает с увеличением Dt. В оптике при w .Амплитуда усредненной гармонической функции быстро убывает с увеличением Dt. В оптике при w |

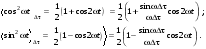 (2.77)
(2.77)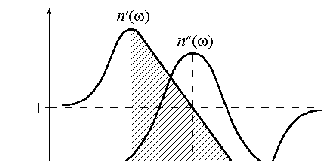
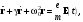 (4.5)
(4.5)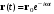 . (4.6)
. (4.6)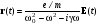 . (4.7)
. (4.7)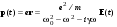 . (4.8)
. (4.8)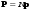 . (4.9)
. (4.9)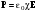 , (4.10)
, (4.10)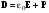 . (4.11)
. (4.11)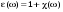 , (4.12)
, (4.12)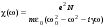 (4.13)или
(4.13)или 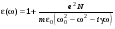 . (4.14)
. (4.14)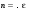 , то это значит, что показатель преломления, а следовательно, и скорость ЭМВ зависят от частоты. Видно также, что n – комплексная величина:
, то это значит, что показатель преломления, а следовательно, и скорость ЭМВ зависят от частоты. Видно также, что n – комплексная величина: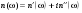 . (4.15)
. (4.15)
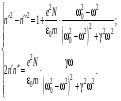 (4.16)
(4.16)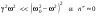 . (4.17)
. (4.17)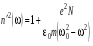 . (4.18)
. (4.18)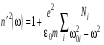 . (4.19)
. (4.19)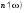 близка к 1 (для прозрачных диэлектриков, разреженных газов):
близка к 1 (для прозрачных диэлектриков, разреженных газов):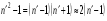 .(4.20)
.(4.20)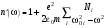 . (4.21)
. (4.21)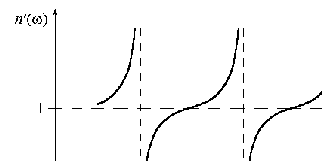 Графическая зависимость
Графическая зависимость 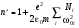 . (4.22)
. (4.22)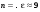 . (Иллюстрация вкладов ионов в дисперсию.))
. (Иллюстрация вкладов ионов в дисперсию.)) 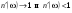 , при этом
, при этом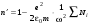 .(4.23)
.(4.23)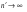 при w = =w0i . Но вблизи собственных частот нельзя пренебречь g. Тогда
при w = =w0i . Но вблизи собственных частот нельзя пренебречь g. Тогда 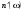 является непрерывной функцией. Разделение мнимых и вещественных частей согласно (4.15) дает (с учетом приближения
является непрерывной функцией. Разделение мнимых и вещественных частей согласно (4.15) дает (с учетом приближения 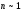 ):
):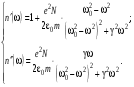 4.24)
4.24)