|
|
1. Оптикой
54 Элементы квантовой теории. Формула Планка не может быть получена в рамках классической теории. Ее строгий вывод можно провести только с точки зрения квантовой теории. Ниже будет продемонстрирован вывод формулы Планка на основе элементарных квантовых представлений об излучении и поглощении света. Пусть оболочка полости тела и излучение в этой полости находятся в термодинамическом равновесии. Предположив, что энергия может излучаться и поглощаться определенными дискретными порциями (квантами), мы должны ввести существование дискретных уровней энергии атома Е2 и Е1, при переходе между которыми и происходит поглощение и испускание света. Рассмотрим атомные переходы с частотой перехода n (или w) между двумя уровнями (индекс 2 – верхний уровень, 1 – нижний):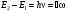 (10.25) (10.25)
В данных процессах можно говорить лишь о вероятности переходов атомов в возбужденное состояние и обратно. В условиях динамического равновесия обмен квантами между уровнями должен быть уравновешен для каждой моды (частоты) в отдельности (принцип детального равновесия). В рассматриваемой системе возможны два типа переходов между уровнями (рис.10.3):
1.Спонтанные переходы.
2.Вынужденные (индуцированные) переходы.
Cпонтанные переходы происходят независимо от падающего на атом излучения и только сверху вниз. Скорость уменьшения числа атомов на верхнем уровне 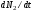 при этом определяется произведением вероятности этого процесса и числа атомов N2 на верхнем уровне: при этом определяется произведением вероятности этого процесса и числа атомов N2 на верхнем уровне:
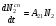 . (10.26) . (10.26)
Коэффициент А21 называется коэффициентом Эйнштейна для спонтанных переходов. Он обратно пропорционален времени жизни атома на этом энергетическом уровне. Спонтанное излучение некогерентно.Вынужденные переходы (как сверху вниз – вынужденное излучение, так и наоборот – вынужденное поглощение) могут происходить только с поглощением кванта энергии, т.е. под влиянием внешнего (индуцирующего) излучения. Скорости изменения количества атомов на соответствующих уровнях при вынужденных переходах определяются через спектральную плотность индуцирующего излучения:
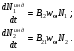 (10.27) (10.27)
Коэффициенты В21 и В12 называются коэффициентами Эйнштейна для вынужденного излучения и вынужденного поглощения соответственно. При вынужденном излучении все характеристики индуцированного и индуцирующего квантов одинаковы (направление, частота, фаза, поляризация), поэтому вынужденные переходы приводят к когерентному излучению системы.
Согласно принципу детального равновесия:
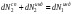 (10.28) (10.28)
Число атомов на уровнях определяется распределением Больцмана:
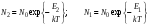 . (10.29) . (10.29)
Подставляя выражения (10.26), (10.27) и (10.29) в (10.28), получаем для спектральной плотности энергии:
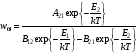 .(10.30) .(10.30)
Но при стремлении температуры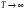 плотность энергии плотность энергии 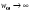 . Это возможно лишь при . Это возможно лишь при 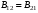 . Поэтому . Поэтому
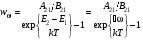 .(10.31) .(10.31)
Отношение коэффициентов Эйнштейна А21/В21 может быть получено только в рамках строгой квантовой теории излучения. Но мы поступим проще. При малых частотах выражение (10.31) должно переходить в формулу Рэлея–Джинса (10.14). Сравнивая эти соотношения, получим:
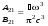 . (10.32) . (10.32)
Подставляя (10.32) в (10.31), получаем окончательно формулу Планка (10.19):
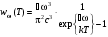 (10.19) (10.19)
55 Инверсия населенностей. В условиях термодинамического равновесия в соответствии и распределением Больцмана концентрация частиц на верхнем уровне всегда меньше, чем на нижнем. Поэтому интенсивность излучения в этом случае уменьшается по мере проникновения вглубь среды согласно закону Бугера. Если же в среде каким-то образом выполнено условие 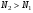 (т.е. создана инверсия населенностей), то интенсивность волны нарастает по мере ее распространения, т.к. при этом переходы с вынужденным излучением происходят чаще, чем поглощательные переходы. При тождественности индуцирующих и индуцированных квантов когерентные свойства светового пучка сохраняются. В этом заключается принцип квантового усилителя. Среда с инверсией населенностей называется активной средой. При создании инверсия населенностей система «активная среда – поле излучения» становится термодинамически неравновесной. (т.е. создана инверсия населенностей), то интенсивность волны нарастает по мере ее распространения, т.к. при этом переходы с вынужденным излучением происходят чаще, чем поглощательные переходы. При тождественности индуцирующих и индуцированных квантов когерентные свойства светового пучка сохраняются. В этом заключается принцип квантового усилителя. Среда с инверсией населенностей называется активной средой. При создании инверсия населенностей система «активная среда – поле излучения» становится термодинамически неравновесной.
Принцип работы лазера (оптического квантового генератора) основан на трех фундаментальных идеях. Первая идея связана с использованием вынужденного испускания света атомными системами. Вторая идея заключается в применении сред с инверсией населенностей, т.е. термодинамически неравновесных систем. Третья идея заключается в использовании в лазере положительной обратной связи для превращения усиливающей системы в генерирующую. В качестве положительной обратной связи (лазерного резонатора) обычно используют систему типа интерферометра Фабри–Перо.
56 Квантовая механика определила дискретность уровней энергии осциллятора. Предельным значением этой энергии является распад осциллятора (ионизация атома), попадание электрона в зону проводимости (внутри металла) и далее. Одним из первых приложений квантовой теории было истолкование законов фотоэффекта.
В 1888 г. Герц обнаружил, что электрический разряд между двумя проводниками происходит значительно сильнее, когда электроды освещаются ультрафиолетовым светом. Физик Гальвакс указал, что это явление обусловлено ионизацией окружающего электроды газа зарядами, вырванными под действием света. В этом же году итальянский физик Аугусто Риги сделал новое открытие: проводящая пластина, освещенная пучком ультрафиолетовых лучей, заряжается положительно. Он же и ввел сам термин «фотоэлектрический эффект», но не смог правильно объяснить это явление. Позднее А.Г.Столетов систематизировал все эти явления на основе опыта, схема которого  приведена на рис.11.1. В исследовании изучалось прохождение тока через конденсатор из двух цинковых пластин при освещении одной из них (катода) светом ртутной лампы. В 1898 г. физики Леннард и Томсон отклонения зарядов в электрическом и магнитном полях определили удельный заряд заряженных частиц, вырываемых светом из катода, совпадающий с известным зарядом электрона e/m. Отсюда следовало, что под действием света происходит вырывание электронов из вещества катода – фотоэлектрический эффект (внешний) (или просто – фотоэффект). приведена на рис.11.1. В исследовании изучалось прохождение тока через конденсатор из двух цинковых пластин при освещении одной из них (катода) светом ртутной лампы. В 1898 г. физики Леннард и Томсон отклонения зарядов в электрическом и магнитном полях определили удельный заряд заряженных частиц, вырываемых светом из катода, совпадающий с известным зарядом электрона e/m. Отсюда следовало, что под действием света происходит вырывание электронов из вещества катода – фотоэлектрический эффект (внешний) (или просто – фотоэффект).
Законы фотоэффекта.
1.При неизменном спектральном составе света сила фототока насыщения прямо пропорциональна падающему на катод световому потоку.
 2.Начальная кинетическая энергия вырванных светом электронов линейно растет с ростом частоты света и не зависит от его интенсивности. 2.Начальная кинетическая энергия вырванных светом электронов линейно растет с ростом частоты света и не зависит от его интенсивности.
3.Фотоэффект не возникает, если частота света меньше некоторой характерной для каждого металла величины nк , называемой красной границей фотоэффекта.
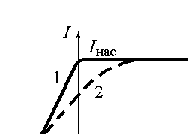
Характерная кривая (вольт-амперная характеристика) для опыта Столетова показана на рис.11.2. В зависимости от условий опыта она может несколько отклоняться от идеализированной кривой 1, но основные характеристики (ток насыщения и задерживающий потенциал) будут одинаковыми, что и иллюстрирует реальная кривая 2 (когда часть вылетевших из катода электронов теряется на пути к аноду).Первый закон фотоэффекта можно объяснить и на основе классической физики. Световое поле, воздействуя на электроны металла, возбуждает их колебания. Амплитуда этих колебаний может достигать значения, при котором электроны покидают металл – наблюдается фотоэффект. Т.к. интенсивность света прямо пропорциональна квадрату электрического поля, то число вырванных электронов растет с увеличением интенсивности света.Второй и третий закон фотоэффекта на основе классической физики объяснить нельзя. Явление фотоэффекта и все его закономерности хорошо объясняются с помощью квантовой теории света и подтверждают ее.
Как уже отмечалось, Эйнштейн в 1905 г., развивая квантовую теорию Планка, выдвинул идею, излучение , поглощение и распространение света происходит порциями (квантами), энергия которых равна 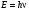 . В этом случае можно записать закон сохранения энергии для элементарного процесса, заключающегося во взаимодействии одного кванта с веществом, сводящегося к передаче электрону дискретного количества энергии. При этом нужно учесть, что электрон в металле не является свободным и, чтобы покинуть металл, электрон должен преодолеть работу выхода A. Применяя к фотоэффекту в металлах закон сохранения энергии, Эйнштейн предложил следующую формулу: . В этом случае можно записать закон сохранения энергии для элементарного процесса, заключающегося во взаимодействии одного кванта с веществом, сводящегося к передаче электрону дискретного количества энергии. При этом нужно учесть, что электрон в металле не является свободным и, чтобы покинуть металл, электрон должен преодолеть работу выхода A. Применяя к фотоэффекту в металлах закон сохранения энергии, Эйнштейн предложил следующую формулу:
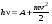 , (11.1) , (11.1)
где A – работа выхода электрона из металла, v – скорость фотоэлектрона. При этом считается, что каждый квант выбивает только один электрон (однофотонный процесс).
Как следует из (11.1), фотоэффект в металлах может возникать только при 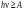 , в противном случае энергии кванта недостаточно для вырывания электрона из металла. Отсюда можно найти минимальную частоту света, при которой происходит фотоэффект (красную границу фотоэффекта): , в противном случае энергии кванта недостаточно для вырывания электрона из металла. Отсюда можно найти минимальную частоту света, при которой происходит фотоэффект (красную границу фотоэффекта):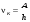 . (11.2) . (11.2)
(Для различных металлов красная граница в длинах волн имеет следующие значения: Zn
370 нм; Na
500 нм; Cs
650 нм.)Пусть между анодом и катодом (рис.11.1) приложен тормозящий потенциал (U < 0) (рис.11.2). Если кинетическая энергия электронов достаточна, то они, преодолев тормозящее поле, все таки создают фототок. В фототоке участвуют те электроны, для которых удовлетворяется условие 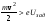 . (11.3) . (11.3)
Величина задерживающего потенциала Uзад определяется из условия: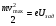 , (11.4) , (11.4)
где vmax – максимальная скорость выбитых электронов. Подставив (11.4) в (11.1), получаем:
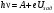 , (11.5) , (11.5)
откуда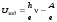 . (11.6) . (11.6)
Т.о., величина задерживающего потенциала не зависит от интенсивности, а зависит только от частоты падающего света, что и объясняет второй закон фотоэффекта. В отличие от металлов в полупроводниках и диэлектриках также возникает так называемый внутренний фотоэффект, состоящий в возбуждении электронов из валентной зоны в зону проводимости. Для внутреннего фотоэффекта энергия поглощенного светового кванта не должна быть меньше ширины запрещенной зоны (разности энергии между нижней границы зоны проводимости и верхней границей валентной зоны).
Применения фотоэффекта.
Фотоэффект очень широко используется в 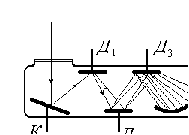 физических приборах. В частности, большое количество фотоприемников основано именно на нем. Самый простой пример – фотоэлемент. Именно с ним и имел дело в опытах по фотоэффекту Столетов. Чувствительность такого прибора можно резко увеличить в фотоумножителях (ФЭУ) (рис.11.3) (коэффициент усиления – до 106). физических приборах. В частности, большое количество фотоприемников основано именно на нем. Самый простой пример – фотоэлемент. Именно с ним и имел дело в опытах по фотоэффекту Столетов. Чувствительность такого прибора можно резко увеличить в фотоумножителях (ФЭУ) (рис.11.3) (коэффициент усиления – до 106).
 Другой пример применения фотоэффекта – электронно-оптические преобразователи (ЭОПы) (рис.11.4), предназначенные для преобразования невидимого излучения (в основном инфракрасного, хотя есть и ЭОПы для ультрафиолетового диапазона), который способен также выполнять функцию усилителя света. Другой пример применения фотоэффекта – электронно-оптические преобразователи (ЭОПы) (рис.11.4), предназначенные для преобразования невидимого излучения (в основном инфракрасного, хотя есть и ЭОПы для ультрафиолетового диапазона), который способен также выполнять функцию усилителя света.
Примеры приборов, использующих внутренний фотоэффект – фотодиоды, солнечные батареи.
57 Вопрос о закономерностях оптических явлений в случае движущихся сред возник в рамках механической волновой теории задолго до создания электромагнитной теории света. Световые волны рассматривались аналогично механическим упругим волнам, поэтому для описания их свойств Гюйгенсом было введено понятие эфира как среды, заполняющее все мировое пространство, в которой распространяются световые волны. Движение тел относительно эфира можно было бы рассматривать как некоторое движение в абсолютной неподвижной системе отсчета. По мере развития механической волновой теории эфир приходилось наделять все более экзотическими характеристиками. Возникшая затем электромагнитная волновая теория Максвелла понятие эфира оставила, превратив его из экзотической материальной среды в условно-абстрактную среду, выполняющую лишь роль системы отсчета, в которой справедливы уравнения Максвелла. Но проблема существования эфира и задача обнаружения этой абсолютной системы отсчета остались актуальными.
Запись законов электродинамики в движущихся средах поставила две основных проблемы, связанных с вопросом перехода от одной инерциальной системы отсчета к другой:
1) как в неподвижной системе отсчета (эфире) выглядят уравнения, описывающие электромагнитные явления, протекающие в движущихся средах;
2) как выглядят уравнения в системе отсчета, движущейся относительно эфира.
При построении теории распространения электромагнитных волн в эфире физики XIX века исходили из двух противоположных точек зрения:
1) эфир полностью увлекается движущимися телами (Герц);
2) эфир неподвижен при движении в нем тел (Лоренц).
Только опыт мог определить, какая из этих точек зрения справедлива. Рассмотрим два основных опыта, проведенные в поисках эфира.
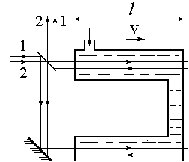
Опыт Физо (1851 г.) опроверг точку зрения Герца о полном увлечении эфира.
Опыт проводился с использованием интерферометрической схемы и сосудом с движущейся водой (рис.12.1). Свет внутри трубок с водой распространяется как по течению воды, так и против течения, v – скорость течения воды, l – длина слоя воды в одном направлении, c’=c/n. Ожидаемый относительный сдвиг интерференционных полос на выходе интерферометра должен быть равен отношению Dt – времени запаздывания одной волны по отношению к другой – к общему периоду колебаний:
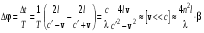 , (12.1) , (12.1)
где b = v/c. В экспериментах Физо действительно наблюдался сдвиг интерференционных полос при переходе от измерений в неподвижной воде к движущейся, но результат получался все время примерно в два раза меньше, т.е. вода при своем движении частично увлекала эфир. Наиболее точные более поздние измерения в модифицированном опыте Физо дали значение
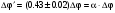 , (12.2) , (12.2)
где коэффициент a, названный коэффициентом увлечения, находился в хорошем соответствии с интуитивно предсказанным ранее Френелем значением:
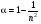 . (12.3) . (12.3)
Строго это соотношение можно объяснить только с точки зрения специальной теории относительности Эйнштейна.
Опыт Майкельсона (1881 г.) был поставлен и неоднократно повторен в целях доказательства второй точки зрения, т.е. в поисках так называемого «эфирного ветра». Пусть интерферометр Майкельсона (см. гл.6) ориентирован так, что одно (1-е) из его одинаковых плеч параллельно направлению скорости орбитального движения Земли, другое (2-е) – перпендикулярно ему. Тогда промежутки времени t1и t2 , которые затрачивает свет для прохождения туда и обратно вдоль плеч оказываются различными:
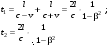 (12.4) (12.4)
Если повернуть прибор на 90о, то разность этих времен изменит знак и наблюдаемые интерференционные полосы должны сместиться. Смещение полос определяется формулой:
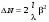 . (12.5) . (12.5)
Но ни самим Майкельсоном ни в более поздних усовершенствованных опытах (в том числе и с использованием лазеров (Таунс, Джаван (1964 г.))) смещения полос обнаружить не удалось.
58 Постулаты Эйнштейна. Отрицательный результат опыта Майкельсона можно было бы объяснить, предположив полное увлечение эфира, но это противоречит опыту Физо. Результаты всех опытов обнаружили противоречия в самом понятии эфира и привели в конце концов к принципу относительности, обобщенному Эйнштейном. Свою систему взглядов он обобщил в двух постулатах:
1. Никакими физическими опытами (механическими, оптическими, электрическими и др. способами) нельзя установить, какая из двух инерциальных систем покоится, а какая движется (принцип относительности).
2. Существует конечная максимальная скорость распространения любого взаимодействия, которая равна с – скорости света в вакууме. По принципу относительности эта скорость постоянна в любой инерциальной системе отсчета
Первый постулат говорит о бесполезности поиска абсолютной системы отсчета, т.е. эфира. Второй постулат отвергает закон классического механического векторного сложения скоростей в экспериментах типа опыта Майкельсона. Сразу отметим, что специальная теория относительности, базирующаяся на этих постулатах, касается только инерциальных систем отсчета.
Анализ операций измерения промежутков времени и расстояний, проведенный в рамках постулатов, привел к необходимости отказаться от представлений классической физики об абсолютном характере таких понятий, как одновременность событий, промежуток времени между событиями, расстояние между точками в пространстве.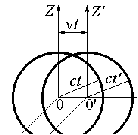
Второй постулат требует уточнения понятия одновременности событий в двух различных инерциальных системах отсчета. Эйнштейн показал, что вследствие этого постулата местное время, введенное в одной инерциальной системе координат, будет отличаться от местного времени во второй инерциальной системе координат. Т.е. очевидное в классической физике соотношение 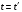 в общем случае не верно. Рассмотрим две инерциальные системы отсчета (рис.12.2), которые в начальный момент времени совпадали, а потом раздвинулись на отрезок vt в направлении X. Если в момент времени в общем случае не верно. Рассмотрим две инерциальные системы отсчета (рис.12.2), которые в начальный момент времени совпадали, а потом раздвинулись на отрезок vt в направлении X. Если в момент времени 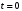 в центре 0 = 0’ возникла сферическая волна, распространяющаяся со скоростью с в вакууме, то через время t будут наблюдаться две сферические волны, что противоречит второму постулату (и опыту!). Волна всегда единственная и сферическая. Для этого должны соблюдаться соотношения: в центре 0 = 0’ возникла сферическая волна, распространяющаяся со скоростью с в вакууме, то через время t будут наблюдаться две сферические волны, что противоречит второму постулату (и опыту!). Волна всегда единственная и сферическая. Для этого должны соблюдаться соотношения:
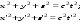 (12.6) (12.6)
Величина 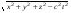 называется интервалом и играет исключительно важную роль в специальной теории относительности. Из (12.6) следует, что при учете однородности и изотропности пространства интервал инвариантен при переходе от одной инерциальной системы отсчета к другой: называется интервалом и играет исключительно важную роль в специальной теории относительности. Из (12.6) следует, что при учете однородности и изотропности пространства интервал инвариантен при переходе от одной инерциальной системы отсчета к другой:
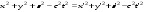 (12.7) (12.7)
Т.о., одним из важнейших следствий постулатов Эйнштейна является то, что пространство и время связаны между собой, образуя четырехмерное пространство–время.Вернемся к вопросу преобразования координат в одномерной задаче рис.12.2. Для координат y и z преобразование наиболее простое, т.к. относительное движение вдоль осей OY и OZ не происходит:
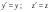 . (12.8) . (12.8)
В самом общем случае величины t, t’, x, x’ могут быть связаны соотношениями:
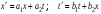 . (12.9) . (12.9)
Подставляя (12.9) в (12.7):
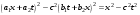 .(12.10) .(12.10)
и приравнивая коэффициенты при одинаковых степенях независимых переменных 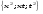 , получаем систему алгебраических уравнений для нахождения коэффициентов в (12.9). Ее решение дает: , получаем систему алгебраических уравнений для нахождения коэффициентов в (12.9). Ее решение дает:
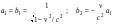 (12.11) (12.11)
Кроме того, из условий движения штрихованной системы координат относительно нештрихованной имеем:
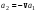 . (12.11’) . (12.11’)
Подставляя (12.11) в (12.9), получаем окончательную форму преобразований Лоренца:
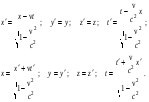 (12.12) (12.12)
Из анализа преобразований Лоренца следуют выводы:
1. Уравнения Максвелла инвариантны относительно преобразований Лоренца.
2. При v << c преобразования Лоренца переходят в классические преобразования Галилея.
3. При 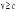 преобразования Лоренца теряют смысл. Следовательно скорость света в вакууме является предельной скоростью любого переноса энергии, в т.ч. и света. Это ограничение касается лишь групповой скорости света, связанной с переносом энергии. преобразования Лоренца теряют смысл. Следовательно скорость света в вакууме является предельной скоростью любого переноса энергии, в т.ч. и света. Это ограничение касается лишь групповой скорости света, связанной с переносом энергии.
Из преобразований Лоренца следуют эффект замедления времени: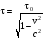 (12.13) (12.13)
и эффект сокращения длины:
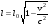 . (12.14) . (12.14)
Длительность процесса, измеренного в системе, относительно которой объект движется, больше, чем в той, относительно которой он покоится. А наибольше значение длина l0 имеет в системе, в которой тело покоится (собственная длина).
Релятивистские эффекты сокращения длины и замедления времени означают лишь, что измеряемый промежуток времени и измеряемая длина зависят от относительного движения. Теория относительности предсказывает влияние движения наблюдателя на результаты измерения.
Рассмотрим с точки зрения преобразований Лоренца интерпретацию опыта Физо. Из преобразований Лоренца имеем:
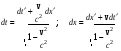 . (12.15) . (12.15)
Тогда для измеряемой на опыте скорости света относительно установки (в лабораторной системе координат) имеем:
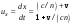 . (12.16) . (12.16)
Здесь учтено, что 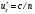 – скорость света относительно воды, v – скорость воды в лабораторной системе координат. В опыте Физо учитывался только эффект первого порядка относительно – скорость света относительно воды, v – скорость воды в лабораторной системе координат. В опыте Физо учитывался только эффект первого порядка относительно 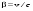 . Тогда . Тогда
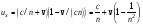 .(12.17) .(12.17)
Это соотношение полностью согласуется с экспериментальными результатами Физо. Видно, что отмеченное в этом опыте френелевское «частичное увлечение эфира» можно рассматривать как простое следствие релятивистской кинематики.
59 Эффект Доплера. Исследуем относительное релятивистское движение источника электромагнитных волн и приемника, которое всегда можно разложить на продольное движение и движение, направление которого перпендикулярно линии, соединяющие исследуемые два тела. Пусть обе системы отсчета инерциальные, дисперсия отсутствует, волна распространяется в вакууме.
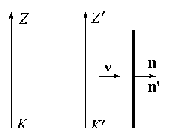 Продольный эффект Доплера.Пусть относительная скорость движения приемника света и излучателя v и нормаль к плоской волне направлены вдоль одной прямой (оси OX) (рис.12.3). Уравнение плоской волны в системе К: Продольный эффект Доплера.Пусть относительная скорость движения приемника света и излучателя v и нормаль к плоской волне направлены вдоль одной прямой (оси OX) (рис.12.3). Уравнение плоской волны в системе К:
 . (12.18) . (12.18)
В системе К’, связанной с приемником света:
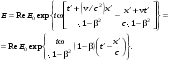 (12.19) (12.19)
С другой стороны в системе К’ уравнение такой плоской волны должно иметь вид:
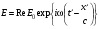 . (12.20) . (12.20)
Сравнивая (12.20) и (12.19), получаем:
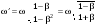 . (12.21) . (12.21)
Если v << c , то пренебрегая членами
b2 , получаем формулу, которой чаще всего и пользуются на практике:
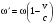 . (12.22) . (12.22)
Сдвигу в область длинных волн (красное смещение) соответствует положительная относительная скорость приемника и излучателя (удаляются друг от друга). При фиолетовом смещении приемник и источник сближаются.
Поперечный эффект Доплера.
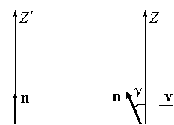
Пусть плоская волна распространяется вдоль оси OZ’, а относительная скорость инерциальных систем направлена вдоль OX (OX’) (рис.12.4). В системе K’, связанной с излучателем, нормаль n к исследуемой волне составляет угол g с направлением OZ. В обеих системах уравнение волны примет вид:
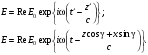 (12.23) (12.23)
Применяя к первому из соотношений (12.23) преобразования Лоренца, получаем:
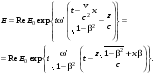 (12.24) (12.24)
Сравнивая (12.24) и второе из соотношений (12.23), получаем:
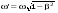 . (12.25) . (12.25)
Разложив в ряд и ограничившись членом
b2, получаем
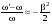 . (12.26) . (12.26)
При фиксации прямого угла между нормалью к волне и скоростью в системе, связанной с приемником, поперечный эффект приводит к красному смещению. При задании прямого угла в системе, связанной с излучателем, наблюдается фиолетовое смещение. Поперечный эффект не меняет знака при изменении знака скорости, т.к. он
b2.
60 Методы определения скорости света.Решение задачи определения скорости света имеет огромное принципиальное и практическое значение. Основная трудность, на которую наталкивается экспериментатор при определении скорости распространения света, связана огромным значением этой величины, требующим совсем иных масштабов опыта, чем те, которые имеют место в классических физических измерениях.Первые научные попытки определения скорости света предпринял Г. Галилей (1607 г.): два наблюдателя А и Б на большом расстоянии друг от друга снабжены закрывающимися фонарями. Наблюдатель А открывает фонарь. Через некоторое время свет доходит до наблюдателя Б, который в тот же момент открывает свой фонарь. Спустя определенное время этот сигнал дойдет до наблюдателя А и он может отметить время t, прошедшее от момента подачи им сигнала до момента его возвращения. Предполагая, что оба наблюдателя реагируют на сигнал мгновенно и свет обладает одной и той же скоростью в обоих направлениях, получим для скорости света выражение: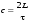 , где L – расстояние между наблюдателями. , где L – расстояние между наблюдателями.
Попытка Галилея не привела ни к каким результатам, т.к. реально измерялось не время распространения светового сигнала, а время, потраченное на реакцию наблюдателя. Немного улучшает ситуацию замена наблюдателя Б зеркалом. При огромной скорости света даже погрешность, вносимая одним наблюдателем, слишком велика. Но принцип проведения данного опыта лежит в основе ряда современных методов измерения скорости света. |
|
|
 Скачать 4.65 Mb.
Скачать 4.65 Mb.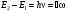 (10.25)
(10.25)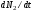 при этом определяется произведением вероятности этого процесса и числа атомов N2 на верхнем уровне:
при этом определяется произведением вероятности этого процесса и числа атомов N2 на верхнем уровне: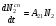 . (10.26)
. (10.26)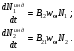 (10.27)
(10.27)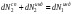 (10.28)
(10.28)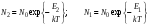 . (10.29)
. (10.29)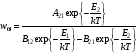 .(10.30)
.(10.30) плотность энергии
плотность энергии  . Это возможно лишь при
. Это возможно лишь при 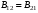 . Поэтому
. Поэтому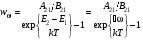 .(10.31)
.(10.31)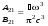 . (10.32)
. (10.32)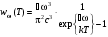 (10.19)
(10.19)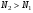 (т.е. создана инверсия населенностей), то интенсивность волны нарастает по мере ее распространения, т.к. при этом переходы с вынужденным излучением происходят чаще, чем поглощательные переходы. При тождественности индуцирующих и индуцированных квантов когерентные свойства светового пучка сохраняются. В этом заключается принцип квантового усилителя. Среда с инверсией населенностей называется активной средой. При создании инверсия населенностей система «активная среда – поле излучения» становится термодинамически неравновесной.
(т.е. создана инверсия населенностей), то интенсивность волны нарастает по мере ее распространения, т.к. при этом переходы с вынужденным излучением происходят чаще, чем поглощательные переходы. При тождественности индуцирующих и индуцированных квантов когерентные свойства светового пучка сохраняются. В этом заключается принцип квантового усилителя. Среда с инверсией населенностей называется активной средой. При создании инверсия населенностей система «активная среда – поле излучения» становится термодинамически неравновесной.  приведена на рис.11.1. В исследовании изучалось прохождение тока через конденсатор из двух цинковых пластин при освещении одной из них (катода) светом ртутной лампы. В 1898 г. физики Леннард и Томсон отклонения зарядов в электрическом и магнитном полях определили удельный заряд заряженных частиц, вырываемых светом из катода, совпадающий с известным зарядом электрона e/m. Отсюда следовало, что под действием света происходит вырывание электронов из вещества катода – фотоэлектрический эффект (внешний) (или просто – фотоэффект).
приведена на рис.11.1. В исследовании изучалось прохождение тока через конденсатор из двух цинковых пластин при освещении одной из них (катода) светом ртутной лампы. В 1898 г. физики Леннард и Томсон отклонения зарядов в электрическом и магнитном полях определили удельный заряд заряженных частиц, вырываемых светом из катода, совпадающий с известным зарядом электрона e/m. Отсюда следовало, что под действием света происходит вырывание электронов из вещества катода – фотоэлектрический эффект (внешний) (или просто – фотоэффект). 2.Начальная кинетическая энергия вырванных светом электронов линейно растет с ростом частоты света и не зависит от его интенсивности.
2.Начальная кинетическая энергия вырванных светом электронов линейно растет с ростом частоты света и не зависит от его интенсивности.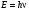 . В этом случае можно записать закон сохранения энергии для элементарного процесса, заключающегося во взаимодействии одного кванта с веществом, сводящегося к передаче электрону дискретного количества энергии. При этом нужно учесть, что электрон в металле не является свободным и, чтобы покинуть металл, электрон должен преодолеть работу выхода A. Применяя к фотоэффекту в металлах закон сохранения энергии, Эйнштейн предложил следующую формулу:
. В этом случае можно записать закон сохранения энергии для элементарного процесса, заключающегося во взаимодействии одного кванта с веществом, сводящегося к передаче электрону дискретного количества энергии. При этом нужно учесть, что электрон в металле не является свободным и, чтобы покинуть металл, электрон должен преодолеть работу выхода A. Применяя к фотоэффекту в металлах закон сохранения энергии, Эйнштейн предложил следующую формулу: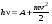 , (11.1)
, (11.1)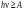 , в противном случае энергии кванта недостаточно для вырывания электрона из металла. Отсюда можно найти минимальную частоту света, при которой происходит фотоэффект (красную границу фотоэффекта):
, в противном случае энергии кванта недостаточно для вырывания электрона из металла. Отсюда можно найти минимальную частоту света, при которой происходит фотоэффект (красную границу фотоэффекта):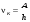 . (11.2)
. (11.2)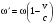 . (12.22)
. (12.22)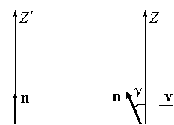
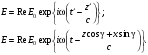 (12.23)
(12.23)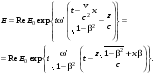 (12.24)
(12.24)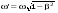 . (12.25)
. (12.25)
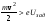 . (11.3)
. (11.3)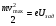 , (11.4)
, (11.4)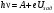 , (11.5)
, (11.5)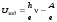 . (11.6)
. (11.6) физических приборах. В частности, большое количество фотоприемников основано именно на нем. Самый простой пример – фотоэлемент. Именно с ним и имел дело в опытах по фотоэффекту Столетов. Чувствительность такого прибора можно резко увеличить в фотоумножителях (ФЭУ) (рис.11.3) (коэффициент усиления – до 106).
физических приборах. В частности, большое количество фотоприемников основано именно на нем. Самый простой пример – фотоэлемент. Именно с ним и имел дело в опытах по фотоэффекту Столетов. Чувствительность такого прибора можно резко увеличить в фотоумножителях (ФЭУ) (рис.11.3) (коэффициент усиления – до 106). Другой пример применения фотоэффекта – электронно-оптические преобразователи (ЭОПы) (рис.11.4), предназначенные для преобразования невидимого излучения (в основном инфракрасного, хотя есть и ЭОПы для ультрафиолетового диапазона), который способен также выполнять функцию усилителя света.
Другой пример применения фотоэффекта – электронно-оптические преобразователи (ЭОПы) (рис.11.4), предназначенные для преобразования невидимого излучения (в основном инфракрасного, хотя есть и ЭОПы для ультрафиолетового диапазона), который способен также выполнять функцию усилителя света.
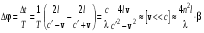 , (12.1)
, (12.1)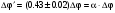 , (12.2)
, (12.2)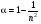 . (12.3)
. (12.3)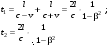 (12.4)
(12.4)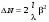 . (12.5)
. (12.5)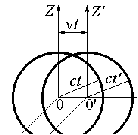
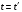 в общем случае не верно. Рассмотрим две инерциальные системы отсчета (рис.12.2), которые в начальный момент времени совпадали, а потом раздвинулись на отрезок vt в направлении X. Если в момент времени
в общем случае не верно. Рассмотрим две инерциальные системы отсчета (рис.12.2), которые в начальный момент времени совпадали, а потом раздвинулись на отрезок vt в направлении X. Если в момент времени 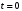 в центре 0 = 0’ возникла сферическая волна, распространяющаяся со скоростью с в вакууме, то через время t будут наблюдаться две сферические волны, что противоречит второму постулату (и опыту!). Волна всегда единственная и сферическая. Для этого должны соблюдаться соотношения:
в центре 0 = 0’ возникла сферическая волна, распространяющаяся со скоростью с в вакууме, то через время t будут наблюдаться две сферические волны, что противоречит второму постулату (и опыту!). Волна всегда единственная и сферическая. Для этого должны соблюдаться соотношения: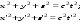 (12.6)
(12.6)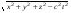 называется интервалом и играет исключительно важную роль в специальной теории относительности. Из (12.6) следует, что при учете однородности и изотропности пространства интервал инвариантен при переходе от одной инерциальной системы отсчета к другой:
называется интервалом и играет исключительно важную роль в специальной теории относительности. Из (12.6) следует, что при учете однородности и изотропности пространства интервал инвариантен при переходе от одной инерциальной системы отсчета к другой: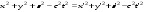 (12.7)
(12.7)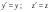 . (12.8)
. (12.8)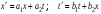 . (12.9)
. (12.9)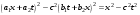 .(12.10)
.(12.10)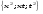 , получаем систему алгебраических уравнений для нахождения коэффициентов в (12.9). Ее решение дает:
, получаем систему алгебраических уравнений для нахождения коэффициентов в (12.9). Ее решение дает: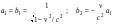 (12.11)
(12.11)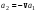 . (12.11’)
. (12.11’)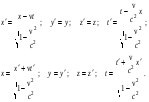 (12.12)
(12.12)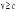 преобразования Лоренца теряют смысл. Следовательно скорость света в вакууме является предельной скоростью любого переноса энергии, в т.ч. и света. Это ограничение касается лишь групповой скорости света, связанной с переносом энергии.
преобразования Лоренца теряют смысл. Следовательно скорость света в вакууме является предельной скоростью любого переноса энергии, в т.ч. и света. Это ограничение касается лишь групповой скорости света, связанной с переносом энергии.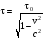 (12.13)
(12.13)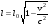 . (12.14)
. (12.14)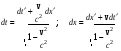 . (12.15)
. (12.15)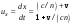 . (12.16)
. (12.16)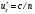 – скорость света относительно воды, v – скорость воды в лабораторной системе координат. В опыте Физо учитывался только эффект первого порядка относительно
– скорость света относительно воды, v – скорость воды в лабораторной системе координат. В опыте Физо учитывался только эффект первого порядка относительно 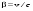 . Тогда
. Тогда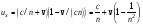 .(12.17)
.(12.17)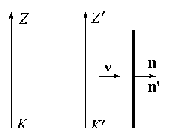
 . (12.18)
. (12.18)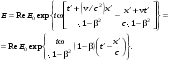 (12.19)
(12.19)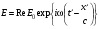 . (12.20)
. (12.20)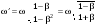 . (12.21)
. (12.21)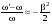 . (12.26)
. (12.26)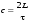 , где L – расстояние между наблюдателями.
, где L – расстояние между наблюдателями.