1. Оптикой
 Скачать 4.65 Mb. Скачать 4.65 Mb.
|
10-10 с) и используется для модуляции оптических пучков, правда, в последнее время крайне редко из-за высоких прикладываемых напряжений.
10 см при поле 1 МА/м) то часто используют для суммарного увеличения угла поворота многократное отражение света между двумя плоскопараллельными зеркалами. Дисперсия постоянной Верде определяется приближенно законом Био:45 Двулучепреломление. Плоскость, проходящая через луч, направленный под углом к оптической оси и оптическую ось, называется главной. Из этого определения и определения главной оси следует, что у луча, вектор E0 которого направлен перпендикулярно главной плоскости, скорость не зависит от направления и равна лучевой скорости, направленной коллинеарно оптической оси. Такой луч называется обыкновенным. Соответствующие ему параметры (скорость, показатель преломления) обозначаются индексом «о». У луча, вектор Eе которого лежит в главной плоскости, скорость зависит от направления, т.к. соответствующая полуось эллипса в сечении эллипсоида изменяется с изменением направления луча. Такой луч называется необыкновенным. Соответствующие ему параметры (скорость, показатель преломления) обозначаются индексом «е». Т.е. показатель преломления необыкновенного луча – величина переменная, зависящая от направления луча. Значение ne, приводящееся для данного кристалла в справочной литературе – это максимально отличающееся от «обыкновенного» показателя преломления noзначение. Кристаллы, для которых 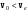 , называются отрицательными, а для которых , называются отрицательными, а для которых 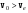 – положительными. Сечения лучевых поверхностей для отрицательных одноосных кристаллов имеют вид: – положительными. Сечения лучевых поверхностей для отрицательных одноосных кристаллов имеют вид: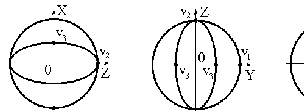 для положительных: 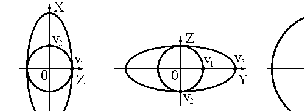 Т.к. внутри кристалла могут распространяться только два луча с различными лучевыми скоростями, то преломление луча на границе с кристаллом приводит в общем случае к возникновению двух лучей внутри кристалла. Такое явление называется двулучепреломлением (1669 г., Бартолинус). 46Построение Гюйгенса производится с помощью лучевых поверхностей (рис.9.6 – для отрицательных кристаллов). Лучевая поверхность строится в единицах 1/n. 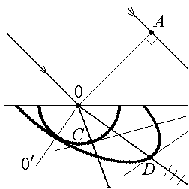 Тогда Тогда 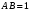 (здесь 1 – это показатель преломления первой среды). Точки C и D – точки пересечения касательных к лучевым поверхностям, т.е. лучи OC и OD – нормали к касательным. (Рассмотреть самостоятельно основные частные случаи). Если луч падает нормально к поверхности кристалла, а оптическая ось параллельна поверхности, то обыкновенный и необыкновенный лучи не разделяются пространственно, а идут нормально поверхности раздела с различными скоростями. На выходе такой плоскопараллельной кристаллической пластины толщиной d волны приобретают разность фаз: (здесь 1 – это показатель преломления первой среды). Точки C и D – точки пересечения касательных к лучевым поверхностям, т.е. лучи OC и OD – нормали к касательным. (Рассмотреть самостоятельно основные частные случаи). Если луч падает нормально к поверхности кристалла, а оптическая ось параллельна поверхности, то обыкновенный и необыкновенный лучи не разделяются пространственно, а идут нормально поверхности раздела с различными скоростями. На выходе такой плоскопараллельной кристаллической пластины толщиной d волны приобретают разность фаз: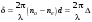 , (9.34) , (9.34)и в результате суперпозиции в общем случае на выходе образуется эллиптически поляризованная волна. Если вектор E в падающей линейно поляризованной волне ориентирован под углом 45o к главной плоскости и параметры пластины 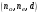 таковы, что таковы, что 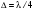 , то вышедший свет будет иметь круговую поляризацию. Такая пластинка называется четвертьволновой; если , то вышедший свет будет иметь круговую поляризацию. Такая пластинка называется четвертьволновой; если 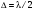 , то на выходе – линейно поляризованная волна с ориентацией вектора E под 90о к ориентации поля E в падающей волне (полуволновая пластинка); если , то на выходе – линейно поляризованная волна с ориентацией вектора E под 90о к ориентации поля E в падающей волне (полуволновая пластинка); если 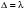 , то поляризация волны не меняется (пластина в целую длину волны). , то поляризация волны не меняется (пластина в целую длину волны).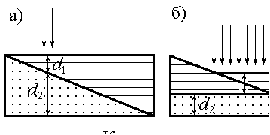 Компенсаторы. Если с помощью четвертьволновой пластинки и дополнительно анализатора можно легко определить, является ли свет естественно поляризованным или циркулярно поляризованным, то для анализа эллиптически поляризованного света (и его отличия от частично поляризованного света, т.е. смеси неполяризованного и линейно поляризованного света) применяют кристаллические устройства, называемые компенсаторами. В общем случае они позволяют компенсировать произвольную разность фаз между обыкновенной и необыкновенной волнами в исследуемом свете, обращая ее в 0, p, 2p или в любое значение. Компенсатор Бабине (рис.9.7а) состоит из двух клиньев, изготовленных из кварца со взаимно перпендикулярными оптическими осями. Луч света в общем случае проходит в клиньях разные пути, соответственно разность хода между обыкновенной и необыкновенной волнами на выходе компенсатора равна: Компенсаторы. Если с помощью четвертьволновой пластинки и дополнительно анализатора можно легко определить, является ли свет естественно поляризованным или циркулярно поляризованным, то для анализа эллиптически поляризованного света (и его отличия от частично поляризованного света, т.е. смеси неполяризованного и линейно поляризованного света) применяют кристаллические устройства, называемые компенсаторами. В общем случае они позволяют компенсировать произвольную разность фаз между обыкновенной и необыкновенной волнами в исследуемом свете, обращая ее в 0, p, 2p или в любое значение. Компенсатор Бабине (рис.9.7а) состоит из двух клиньев, изготовленных из кварца со взаимно перпендикулярными оптическими осями. Луч света в общем случае проходит в клиньях разные пути, соответственно разность хода между обыкновенной и необыкновенной волнами на выходе компенсатора равна: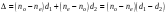 . (9.35) . (9.35)Зная толщины 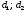 в месте падения на компенсатор волны, можно найти вносимую дополнительную разность фаз. Недостатком компенсатора Бабине является то, что он может работать только с узкими пучками света, а изменение разности хода производится перемещением пучка в поперечном направлении. Этого недостатка лишен компенсатор Солейля (рис. 9.7б), состоящий из кварцевых двух клиньев и прямоугольной пластинки. Расположение оптических осей показано на рисунке. Передний клин может перемещаться параллельно по поверхности другого клина с помощью микрометрического винта. Разность хода так же определяется по формуле (9.35). Т.к. оптические оси в клиньях параллельны, то такой компенсатор может работать с широкими пучками света. в месте падения на компенсатор волны, можно найти вносимую дополнительную разность фаз. Недостатком компенсатора Бабине является то, что он может работать только с узкими пучками света, а изменение разности хода производится перемещением пучка в поперечном направлении. Этого недостатка лишен компенсатор Солейля (рис. 9.7б), состоящий из кварцевых двух клиньев и прямоугольной пластинки. Расположение оптических осей показано на рисунке. Передний клин может перемещаться параллельно по поверхности другого клина с помощью микрометрического винта. Разность хода так же определяется по формуле (9.35). Т.к. оптические оси в клиньях параллельны, то такой компенсатор может работать с широкими пучками света.Использование анизотропии для создания поляризаторов. Прибор для получения линейно поляризованного света называется поляризатором. Если такой же прибор предназначен для анализа состояния поляризации света, то он называется анализатором. Явление анизотропии и, в частности, двулучепреломление часто используется для получения и анализа поляризованного света. а) Поглощение света в дихроичных пластинках. У некоторых двулучепреломляющих кристаллов (например, турмалина) коэффициенты поглощения света для двух взаимно перпендикулярно поляризованных волн отличаются настолько сильно, что уже при небольшой толщине кристалла одна из волн гасится практически полностью и из кристалла выходит линейно поляризованный пучок света. Это явление называется дихроизмом. Дихроизм является частным случаем плеохроизма (многоцветности) (чаще называют полихроизмом) – изменения окраски вещества в проходящем свете в зависимости от направления и поляризации этого света (отметим, что рубин является типичным полихроичным кристаллом). В настоящее время дихроичные пластинки изготовляют в виде тонких пленок – поляроидов, имеющих широкое применение. В большинстве случаев они состоят из множества мелких (толщиной до 0,3 мм) параллельно ориентированных кристаллов сернокислого йодистого хинина – герапатита, находящихся внутри связующей среды – прозрачной пленки. Недостатки поляроидов связаны со спектральной селективностью поглощения герапатита, из-за чего фиолетовая часть спектра оказывается поляризованной лишь частично, а пленка получается неодинаково прозрачной для различных длин волн. б) Поляризационные и двоякопреломляющие призмы. Как мы уже убедились, преломляясь в кристалле, световой луч разделяется на два линейно поляризованных луча со взаимно перпендикулярными направлениями колебаниями вектора E. Обыкновенный луч удовлетворяет обычному закону преломления Снеллиуса. Для необыкновенного луча показатель преломления среды и отношение синусов углов падения и преломления не остается постоянным при изменении угла падения. Отклоняя один из лучей в сторону каким-либо способом (например, используя полное внутреннее отражение, конфигурацию кристалла или склейку нескольких кристаллов), можно получить линейно поляризованную волну. Призма называется поляризационной, когда на ее выходе имеется одна поляризованная волна, а двоякопреломляющей, если на выходе имеются обе ортогонально поляризованные волны. Отличительной чертой таких кристаллических призменных поляризаторов является высокая степень поляризации по сравнению с другими типами поляризаторов. Как правило, в поляризационных призмах за счет конфигурации кристаллов и типа их склейки создаются условия полного отражения для одной из поляризованной волн. Примеры поляризационных призм (рис.9.8): призмы Николя, Глана-Томсона (склейка канадским бальзамом, у которого значение показателя преломления n=1,55 лежит между показателем преломления обыкновенного nо=1,658и необыкновенного nе=1,486лучей), призма Глана (воздушная склейка). В 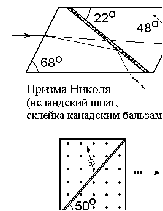 двоякопреломляющих призмах склейки нет, но оптические оси в разных частях призмы повернуты друг относительно друга. Пример: призма двоякопреломляющих призмах склейки нет, но оптические оси в разных частях призмы повернуты друг относительно друга. Пример: призма 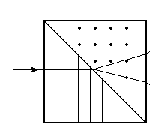 Волластона (рис.9.9). Волластона (рис.9.9).49 Вращение плоскости поляризации. Ряд веществ обладают способностью поворачивать плоскость поляризации прошедшего через них света. Такие вещества называются оптически активными (гиротропными). Типичным представителем оптически активного вещества является кварц. В нем этот эффект наблюдается, когда свет проходит вдоль оптической оси, т.е. когда не происходит двулучепреломление. Впервые вращение плоскости поляризации обнаружил Араго (Arago Dominique Francois Jean, 1786–1853) именно в кварце в 1811 г. Экспериментально установлено, что угол поворота зависит от длины пути d в кристаллической пластинке и от длины волны: 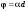 , (9.36)где , (9.36)где 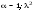 –коэффициент пропорциональности, называемый вращательной способностью. Вращательная способность кварца весьма велика и лежит в диапазоне от 15°/мм для красной области спектра до 51°/мм в фиолетовой области спектра. Существуют две модификации кварца – правовращающая и левовращающая. Различие в направлениях вращения связаны с зеркально отображенной кристаллической структурой в этих модификациях. Гиротропными свойствами обладают и многие аморфные вещества (сахароза, камфора, патока, никотин, скипидар). Этим веществам также присущи две модификации направлений вращения. Для растворов гиротропных веществ справедлив закон Био: –коэффициент пропорциональности, называемый вращательной способностью. Вращательная способность кварца весьма велика и лежит в диапазоне от 15°/мм для красной области спектра до 51°/мм в фиолетовой области спектра. Существуют две модификации кварца – правовращающая и левовращающая. Различие в направлениях вращения связаны с зеркально отображенной кристаллической структурой в этих модификациях. Гиротропными свойствами обладают и многие аморфные вещества (сахароза, камфора, патока, никотин, скипидар). Этим веществам также присущи две модификации направлений вращения. Для растворов гиротропных веществ справедлив закон Био: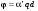 , (9.37) , (9.37)где q – концентрация раствора, 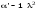 – постоянная вращения (удельная вращательная способность) для данного вещества, сильно зависящая от длины волны, слабо – от температуры вещества и практически не зависит от агрегатного состояния вещества. – постоянная вращения (удельная вращательная способность) для данного вещества, сильно зависящая от длины волны, слабо – от температуры вещества и практически не зависит от агрегатного состояния вещества.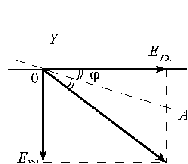 Элементарная феноменологическая теория вращения плоскости поляризации. Интерпретация гиротропии впервые была дана Френелем (1817 г.). В главе 2 мы уже установили, что волну с линейной поляризацией можно разложит на две волны с круговой поляризацией с левым и правым вращением. Френель предположил, что в гиротропном веществе скорости распространения циркулярно поляризованных в разных направлениях волн различны. В соответствии эти все гиротропные вещества делятся на правовращающие и левовращающие. Разложим изначально линейно поляризованную в плоскости XZ волну на две циркулярно поляризованные и запишем покоординатно эти циркулярно поляризованные волны с векторами Elи Er, распространяющиеся в направлении оси Z с коэффициентами преломления nl и nr. На выходе гиротропной среды толщиной d имеем (рис.9.10): Элементарная феноменологическая теория вращения плоскости поляризации. Интерпретация гиротропии впервые была дана Френелем (1817 г.). В главе 2 мы уже установили, что волну с линейной поляризацией можно разложит на две волны с круговой поляризацией с левым и правым вращением. Френель предположил, что в гиротропном веществе скорости распространения циркулярно поляризованных в разных направлениях волн различны. В соответствии эти все гиротропные вещества делятся на правовращающие и левовращающие. Разложим изначально линейно поляризованную в плоскости XZ волну на две циркулярно поляризованные и запишем покоординатно эти циркулярно поляризованные волны с векторами Elи Er, распространяющиеся в направлении оси Z с коэффициентами преломления nl и nr. На выходе гиротропной среды толщиной d имеем (рис.9.10):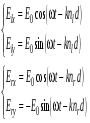 (9.38) При различных коэффициентах преломления векторы Elи Er после прохождения среды уже расположены симметрично не относительно оси X, а относительно линии 0А и определяющей угол поворота. Найдем ее положение. В момент времени 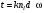 имеем: имеем: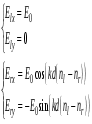 (9.39) (9.39)Следовательно плоскость поляризации поворачивается на угол 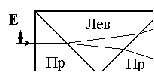 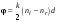 . (9.40) . (9.40)Существование в кварце волн с круговой поляризацией экспериментально подтвердил Френель в опыте с составной призмой из левовращающего и правовращающего кварца (рис.9.11). Отличие скоростей распространения циркулярно поляризованных волн может быть объяснено только с точки зрения кристаллического или молекулярного строения вещества. В случае кристаллов основной причиной различия скоростей является асимметрия кристаллической структуры (отсутствие центра симметрии). Для аморфных тел это явление может быть связано со строением сложных молекул гиротропной среды (например, спиралевидной). Вращение плоскости поляризации в магнитном поле (эффект Фарадея). При приложении магнитного поля к оптически неактивной среде она становится гиротропной. Это эффект был открыт Фарадеем в 1845 г. Угол поворота плоскости поляризации определяется формулой: 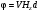 , (9.41) , (9.41)где V – постоянная Верде, характеризующая свойства вещества, Hz– проекция вектора напряженности магнитного поля на направление распространения света. Знак угла поворота плоскости поляризации не зависит от направления распространения света, а определяется направлением магнитного поля. Т.к. величина постоянной Верде достаточно мала (для большинства твердых тел угол составляет |
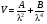 , (9.42)
, (9.42)где постоянные А и B слабо зависят от температуры.
В ферромагнитных материалах угол поворота обычно выражают не через магнитное поле, а через намагниченность:
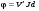 , (9.43)
, (9.43)где коэффициент пропорциональности V’ называется постоянной Кундта.
Эффект Фарадея совместно с поляризаторами используют для модуляции света и для создания однонаправленного распространения света (т.н. оптических изоляторов).
50 Эффекты искусственной анизотропии. Оптически изотропная среда при внешнем воздействии может становиться анизотропной. Такая искусственная анизотропия может быть вызвана механической деформацией, приложением внешнего электрического или магнитного полей. При механической деформации вызывающее эту деформацию напряжение
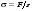 определяет разницу между обыкновенным и необыкновенным показателем преломления:
определяет разницу между обыкновенным и необыкновенным показателем преломления: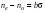 , (9.44)
, (9.44)где b – постоянная, определяющая отклик вещества на механическое напряжение. Во внешнем электрическом поле изотропное вещество приобретает свойства одноосного кристалла с оптической осью, направленной вдоль вектора напряженности внешнего электрического поля E, причем разность показателей преломления пропорциональна квадрату амплитуды этого поля (эффект Керра):
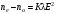 , (9.45)
, (9.45)где К – постоянная Керра (для жидкостей эта величина

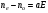 ,(4.46)где а – пост. величина.
,(4.46)где а – пост. величина.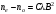 ,(4.47)
,(4.47)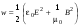 . (10.1)
. (10.1)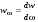 . (10.2)
. (10.2)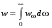 . (10.3)
. (10.3)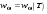 . (10.4)
. (10.4)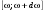 ко всей энергии излучения, падающей за 1 с в том же интервале частот на этот участок. Падающее излучение – изотропно.
ко всей энергии излучения, падающей за 1 с в том же интервале частот на этот участок. Падающее излучение – изотропно.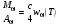 , (10.5)
, (10.5) Коэффициент с/4 получается после интегрирования по телесному углу. Абсолютно черным телом называется тело, полностью поглощающее всё падающее на него излучение, т.е.
Коэффициент с/4 получается после интегрирования по телесному углу. Абсолютно черным телом называется тело, полностью поглощающее всё падающее на него излучение, т.е. 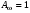 и
и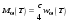 .(10.6)
.(10.6)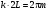 (10.7)
(10.7)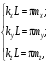 (10.8)
(10.8)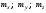 – целые числа.
– целые числа.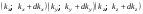 равно числу целых чисел в интервале
равно числу целых чисел в интервале 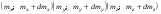 . Отсюда следует, что
. Отсюда следует, что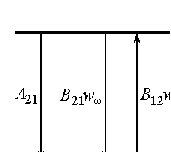
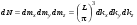 . (10.9)
. (10.9)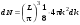 . (10.10)
. (10.10)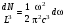 (10.11)
(10.11)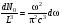 – (10.12)
– (10.12)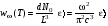 , (10.13)
, (10.13)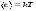 , где k – постоянная Больцмана. Тогда
, где k – постоянная Больцмана. Тогда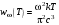 – формула Рэлея-Джинса.(10.14)
– формула Рэлея-Джинса.(10.14)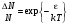 . (10.15)
. (10.15)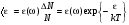 (10.16)
(10.16)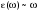 . Гораздо позже был найден коэффициент пропорциональности – постоянная Планка:
. Гораздо позже был найден коэффициент пропорциональности – постоянная Планка: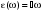 . (10.17)
. (10.17)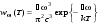 .Формула Ви (10.18)
.Формула Ви (10.18)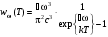 Форм. Планка(10.19)
Форм. Планка(10.19)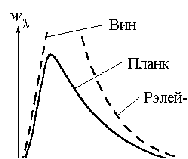 Эта формула полностью описывает излучение АЧТ и в предельных переходах формулы Рэлея–Джинса и Вина хорошо с ней согласуются (рис.10.2).
Эта формула полностью описывает излучение АЧТ и в предельных переходах формулы Рэлея–Джинса и Вина хорошо с ней согласуются (рис.10.2).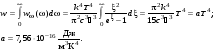 (10.20)
(10.20)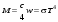 З. Стефана – Больцмана.(10.21)
З. Стефана – Больцмана.(10.21)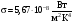 – постоянная Стефана – Больцмана. (10.22)
– постоянная Стефана – Больцмана. (10.22)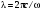 :
: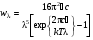 . (10.23)
. (10.23)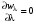 . Получаем:
. Получаем: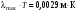 З. смещения Вина.(10.24)
З. смещения Вина.(10.24)