39 Разрешающая способность дифракционной решетки. Для количественной оценки разрешающей способности дифракционных спектральных приборов служит критерий Рэлея: две спектральные линии являются разрешенными, если максимум дифракционной картины для одной длины волны совпадает с ближайшим минимумом для другой длины волны. Вспомним, что для интерферометра Фабри-Перо мы воспользовались близким следствием из критерия Рэлея – пересечением двух соседних максимумов в интерференционной картине на полувысоте. Часто пользуются еще одним следствием из критерия Рэлея – при равной интенсивности исследуемых симметричных максимумов глубина провала между «горбами» составляет 20% от максимума. Конечно, эти следствия, как, впрочем, и сам критерий Рэлея являются достаточно условными. Но они позволяют вполне объективно оценить границу разрешения данного спектрального прибора.
Найдем разрешающую способность дифракционной решетки исходя из критерия Рэлея. Между главными максимумами дифракционной картины располагаются N – 1 минимум, где N – общее число щелей, участвующее в дифракции. Тогда критерий Рэлея запишется в виде:
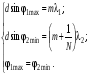 (7.66) (7.66)
Тогда разрешающая способность дифракционной решетки g равна: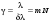 . (7.67) . (7.67)
Переход от интерференции двух волн к многолучевой интерференции приводит к концентрации излучения вблизи определенных направлений и к увеличению темных промежутков между максимумами, т.е. к увеличению разрешающей способности.
Дисперсионная область дифракционной решетки ищется точно так же, как и для интерферометра Фабри-Перо, т.е. по формуле (6.46):
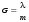 . (7.68) . (7.68)
Сравнение характеристик спектральных аппаратов. Высокая разрешающая способность в спектральных приборах типа ИФП (
106) и дифракционной решетки (
105) достигается за счет различных факторов. В ИФП – за счет высоких порядков интерференции (из-за достаточно большой базы интерферометра) при сравнительно небольшом числе интерферирующих волн (нескольких десятков). В дифракционной решетке все наоборот – высокая разрешающая способность достигается за счет большого числа интерферирующих волн при малом порядке интерференции. С другой стороны, порядок интерференции (см. (6.46) и (7.68)) определяет малое значение дисперсионной области для ИФП (
10-2 нм) и большое его значение для дифракционной решетки (
103 нм). Поэтому для получения оптимальных характеристик в эксперименте используют комбинацию различных спектральных приборов. Недостатком дифракционной решетки является малая интенсивность выходного сигнала. ИФП лишен этого недостатка.
40 Голографией называют метод записи и последующего восстановления пространственной структуры световых волн, основанный на явлениях интерференции и дифракции когерентных пучков света. Как и фотография, она обеспечивает возможность записи, хранения и воспроизведения зрительных образов предметов. Фотопластинка, на которой записана эта информация, называется голограммой. В отличие от фотографии голография позволяет записать и восстановить не двухмерное распределение освещенности в плоскости снимка, а рассеянные предметом световые волны со всеми их характеристиками – направлением распространения, 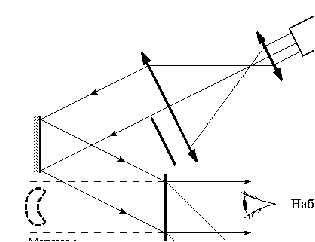 амплитудой, фазой, длиной волны. Восстановленные голограммой световые волны создают полную иллюзию реальности наблюдаемых предметов. амплитудой, фазой, длиной волны. Восстановленные голограммой световые волны создают полную иллюзию реальности наблюдаемых предметов.
На голограмме регистрируется не оптическое изображение объекта, а интерференционная картина, возникающая при наложении световой волны, рассеянной объектом (предметной волны), и когерентной с ней опорной (или референтной) волны.
Рассмотрим двухлучевую схему голографии (рис.8.1). Исследуемый объект освещают расширенным с помощью телескопа пучком света лазера. Рассеянная объектом световая волна, а также опорная, отраженная от зеркала, попадают на фотопластинку, на которой регистрируется возникающая интерференционная картина. Дальше пластинка проявляется обычным способом. Получающуюся на голограмме упорядоченную интерференционную структуру можно рассмотреть только с помощью микроскопа.
Для восстановления волны убирают исследуемый объект и помещают голограмму на то место, где находилась фотопластинка (рис.8.2). Освещая ее светом однотипного лазера, наблюдают через голограмму изображение объекта, которое получается там же, где находился объект. Наблюдатель видит «мнимое» изображение предмета как сквозь дымчатое стекло. Причем, т.к. в голограмме зафиксирована вся информация о предмете, то объект воспринимается объемно. Кроме «мнимого», есть и «действительное изображение», имеющее обратный рельеф наблюдаемой поверхности.
Пусть требуется зарегистрировать плоский волновой фронт с волновым вектором k1 , нормальным к оси X и направленным под углом j к оси Z (рис.2). Поместим в плоскость XOY фотопластинку. В этой плоскости распределение поля имеет вид:
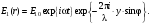 (8.1) (8.1)
Если зафиксировать на фотопластинке соответствующую (8.1) интенсивность, то мы получим обычное фотографическое «изображение» плоской волны – пластинка будет равномерно засвечена. Сохранить же информацию о фазе волны позволяет добавление опорной волны. Пусть плоская опорная волна E2направлена вдоль Z. Тогда распределение интенсивности на пластинке примет вид:
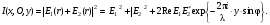 (8.2) (8.2)
Распределение интенсивности представляет собой периодическую систему полос, параллельных оси X с пространственным периодом l/sinj. После проявки фотопластинки получается плоская дифракционная решетка с синусоидальным законом амплитудного пропускания (правда, если амплитудное пропускание линейно связано с освещенностью фотопластинки). Это и есть голограмма исходной плоской волны. Освещение такой решетки плоской волной, тождественной опорной волне, приводит к появлению двух дифрагированных плоских волн по углами ±j1 к оси Z (т.е. дифракционных максимумов) (см. гл.7):
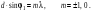 (8.3) (8.3)
Т.о., освещение тонкослойной голограммы только опорной волной приводит к появлению как предметной, так и паразитной волны, симметричной исходной. Ее возникновение связано с тем, что на обычной голограмме не фиксируется направление записываемой волны: голограмма не изменится, если эта волна распространяется в противоположном направлении. Рассматриваемые далее толстослойные голограммы этим недостатком не обладают.
Аналогично можно вместо плоской волны рассмотреть получение голограммы сферической волны. В этом случае при плоском опорном фронте мы получим голограмму в виде синусоидальной зонной пластинки, которая при облучении плоской волной дает изображение точки – источника сферической волны. Другими словами, зонная пластинка является голограммой точки. Разбивая произвольный объект на совокупность независимых точечных источников, для каждого из которых справедливы эти рассуждения, мы приходим к описанию голограммы произвольного поля через наложение множества зонных пластинок Френеля.
 Отметим, что каждый участок голограммы способен восстановить изображение всего объекта, но качество изображения при уменьшении площади голограммы ухудшается. Отметим, что каждый участок голограммы способен восстановить изображение всего объекта, но качество изображения при уменьшении площади голограммы ухудшается.
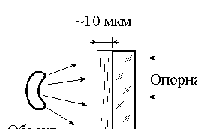
До сих пор мы рассматривали способ записи и воспроизведения так называемых тонкослойных голограмм. В 1962 г. советский ученый Ю.Н. Денисюк осуществил метод записи и воспроизведения голограммы в трехмерной среде. В этом методе используются толстослойные (порядка нескольких десятков микрометров) фотопластинки. Схема записи такой голограммы при встречных пучках (опорной и предметной волны) за счет образования в толще фотоэмульсии стоячей волны показана на рис.8.3. После экспозиции при облучении монохроматическим светом в результате дальнейшей химической обработки в фотоэмульсии получается трехмерная дифракционная решетка с полупрозрачными отражающими слоями серебра (так называемыми слоями Липпмана). Если затем полученную голограмму осветить опорной волной, то частично отраженные от слоев Липпмана когерентные световые волны, интерферируя, дадут изображение предмета в исходном положении. Интерференционное усиление происходит в том случае, когда отраженные от слоев волны синфазны, т.е. удовлетворяют так называемому условию Вульфа-Брэгга:
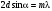 , (8.4) , (8.4)
где d – расстояние между слоями Липпмана, a – угол скольжения отраженной брэгговской волны, m – целые числа.
Выполнение этого условия приводит к избирательности голограммы по отношению к длине восстанавливающей опорной волны. Т.к. трехмерная решетка пропустит (точнее, отразит) излучение только той длины волны монохроматического света, под действием которого она записывалась (то же самое можно отметить и о направлении a), то можно восстанавливать изображение, используя источник сплошного спектра. Если исходные опорная и предметная волны содержали несколько длин волн, то с фотоэмульсии возникнет несколько пространственных решеток. При освещении таким образом записанной голограммы источником сплошного света (например, солнечного или от лампы накаливания) можно получить объемное цветное изображение.
Основные области применения голографии:
Запись и хранение информации, в т.ч. и визуальной (оптическая голографическая память). На голографическую пластинку размером 32´32 мм2 можно записать 1024 голограммы, каждая по 1 мм2 и содержит, например, одну страницу текста. В толстослойной голограмме можно производить независимую запись и аналогично восстановление, изменяя угол падения опорной волны. В зависимости от типа записывающей среды память может быть как постоянной, так и стираемой. В тонких оптических средах могут быть записаны примерно 108 бит/см2, а при использовании объемной голографии теоретически можно запомнить примерно до 1010 бит/см3. Сюда же можно отнести и всевозможные художественные применения голографии (объемные изображения музейных предметов, голографическое кино, объемные портреты и т.д.)
Оптическая обработка информации и системы распознавания образов (распознавание знаков, языка, отпечатков пальцев, изображений). Сравнение объекта (например, корреляционным методом) ведется с записанными голограммами известных объектов. Корректировка и обработка изображений может быть проведена с помощью определенных голографических фильтров.
Голографическая интерферометрия. Этот метод позволяет исследовать изменения (например, деформацию), происшедшие в наблюдаемом объекте под каким-либо внешним воздействием. В основе регистрации таких малых деформаций лежит явление интерференции двух волн, существовавших в разные моменты времени и записанных на одну голограмму. По полученной полосатой интерференционной картине можно определить изменения до десятых долей микрометра. С помощью голографической интерферометрии возможно измерение всех видов деформации прозрачных и непрозрачных тел; очень малых перемещений; типов колебаний; распределений температуры; произвольных распределений неоднородностей. Этот метод на практике применяют для исследований частей машин; деталей кузова автомобилей; автомобильных шин и других легко деформируемых тел; оптических элементов; музыкальных инструментов; распределения неоднородностей в атмосфере и других средах; плазмы.
41 Описание анизотропных сред. Оптической анизотропией называется зависимость оптических свойств среды от направления распространения света в ней. Физическая природа анизотропии вещества связана с особенностями строения его молекул или особенностями кристаллической решетки, в узлах которой находятся атомы или ионы. Взаимодействие света с веществом для анизотропных сред не может быть моделировано колебаниями одного осциллятора. Для описания таких сред необходимо ввести три различных взаимно перпендикулярных осциллятора и характеризовать три взаимно перпендикулярных направления различными значениями показателя преломления. Однако изучение распространения света в анизотропных средах мы будем строить не на учете атомной структуры среды, а с помощью феноменологической электромагнитной теории. В рамках этой теории анизотропия учитывается тем, что в материальном уравнении диэлектрическая восприимчивость c(w) представляет собой тензор, а не скаляр, как для изотропной среды. Анизотропию магнитных свойств сред мы рассматривать не будем, т.к., во-первых, принцип описания будет точно таким же, и, во-вторых, магнитная анизотропия используется значительно реже.
В анизотропной среде проекции поляризованности связаны с проекциями напряженности электрического поля соотношениями:
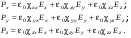 (9.1) (9.1)
В дальнейшем для простоты будем нумеровать декартовы оси координати соответствующие им проекции числами или индексами 1, 2, 3. Матрица величин cij называется тензором диэлектрической восприимчивости. Тогда систему (9.1) можно записать в компактном виде: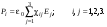 (9.2) (9.2)
Соотношение между компонентами вектора электрического смещения D и поляризованностью P для анизотропной среды принимает вид:
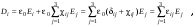 (9.3) (9.3)
где dij – символ Кронекера. Тензор eij :
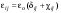 (9.4) (9.4)
называется тензором диэлектрической проницаемости.
Рассмотрим основные его свойства. Запишем выражение для плотности электрической энергии w с учетом (9.3):
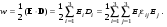 (9.5) (9.5)
Изменим порядок индексов в (9.5):
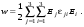 (9.6) (9.6)
Вычитая почленно (9.6) из (9.5), получим:
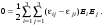 (9.7) (9.7)
Отсюда следует, что т.к. проекции поля E независимы, то тензор диэлектрической проницаемости является симметричным: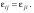 (9.8) (9.8)
Воспользуемся математическими свойствами полученных выражений. Т.к. плотность электрической энергии положительна, то стоящая в правой части (9.5) квадратичная форма является положительно определенной.
Замечание.
Формой степени n (или однородным многочленом) называется многочлен от нескольких переменных, каждый член которого имеет степень n относительно совокупности всех переменных.
Действительную квадратичную форму f(x1, x2, ... xn=ååaijxixj называют положительно определенной, если f > 0 для любого набора значений переменных x1, x2, ..., xn, среди которых есть хотя бы одно, отличное от нуля.
Перейдя к новым переменным:
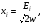 (9.9) (9.9)
выражение (9.5) можно записать в виде:
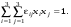 (9.10) (9.10)
Как известно из математики, с помощью преобразования системы координат такая форма может быть приведена к виду:
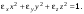 (9.11) (9.11)
Полученные таким образом оси X, Y, Zновой системы координат называют главными осями тензора диэлектрической проницаемости (в дальнейшем мы их так и будем обозначать большими буквами). В главной системе координат тензор диэлектрической проницаемости является диагональным:
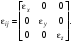 (9.12) (9.12)
Уравнение (9.11) описывает эллипсоид с полуосями, расположенными вдоль главных осей тензора и равными ex-1/2, ey-1/2, ez-1/2. В главных осях соотношение (9.3) примет вид:
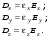 (9.13) (9.13)
Т.к. в общем случае элементы тензора диэлектрической проницаемости неодинаковы, то в анизотропной среде векторы D и E не коллинеарны.
42 Распространение плоской электромагнитной волны в анизотропной среде. Подставляя векторы E, D, H, B в плоской ЭМВ в виде
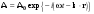 (9.14) (9.14)
в уравнения Максвелла (2.1) — (2.6), получим следующие соотношения между векторами полей и волновым вектором k :
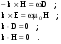 (9.15) (9.15)
Волновой вектор k показывает направление распространение волнового фронта, т.е. фазовая скорость v направлена вдоль волнового вектора. Введем единичный 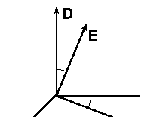 вектор направления распространения волны n: вектор направления распространения волны n: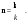 (9.16) (9.16)
Поток энергии, по определению, распространяется по направлению вектора Пойнтинга S = E´H . Направление потока энергии в волне называется лучом. Т.к. энергия ЭМВ распространяется с групповой скоростью, то групповая скорость u направлена вдоль луча. Введем единичный вектор в направлении распространения луча:
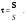 (9.17) (9.17)
Т.к. а анизотропной среде векторы E и D не коллинеарны, то направления распространения волны и луча не совпадают. Соответственно не совпадают по направлению групповая и фазовая скорость. Ориентация между векторами в ЭМВ изображена на рис. 9.1. Вектора D, E, n, t лежат в одной плоскости, перпендикулярной H. Из (9.15) — (9.17) следует: n ^ D; t ^ E . Угол между D и E равен углу между n и t.
Вектор E , оставаясь перпендикулярным H, не перпендикулярен направлению распространения фазы волны. В этом смысле волна в кристалле не является строго поперечной, т.к. имеется отличная от нуля проекция вектора E на направление n и соответственно проекция D на направление t. Лишь при ориентации вдоль одной из главных осей кристалла вектор D коллинеарен вектору E.
Плоскость равных фаз перемещается вдоль вектора n со скоростью v. Скорость перемещения этой плоскости вдоль вектора луча t называется лучевой скоростью.
Особенности распространения лучей в анизотропной среде обусловлены как дисперсией волн, так и отличием направлений волновых нормалей и лучей. Дисперсия в равной мере присуща как изотропным, так и анизотропным средам. Но чтобы выделить особенности именно анизотропии, в дальнейшем будем пренебрегать дисперсией. В такой недиспергирующей анизотропной среде понятия лучевой скорости и групповой скорости совпадают. Получим выражение для зависимости фазовой скорости от направления распространения волны и плоскости поляризации. Воспользуемся первыми двумя уравнениями в (9.15) и формулой разложения двойного векторного произведения. Тогда получаем уравнение:
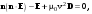 (9.18) (9.18)
где v = w/k – фазовая скорость. В главной системе координат с учетом (9.13) (9.18) в скалярном виде преобразуется в систему трех уравнений:
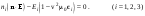 (9.19) (9.19)
Здесь ni – направляющие косинусы направления волны относительно соответствующей главной оси. Пусть E направлен, например, вдоль главной оси X. Тогда с учетом (9.13) система (9.19) сводится к одному уравнению
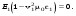 (9.20) (9.20)
При ненулевом поле E получаем: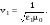 (9.21) (9.21)
Аналогичные рассмотрения случаев, когда E (и соответственно D) направлено или вдоль Y или вдоль Z, позволяют найти остальные значения vi :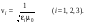 (9.22) (9.22)
Полученные скорости vi называются главными скоростями распространения волны.
Необходимо отметить, что:
vi – это не проекции вектора фазовой скорости на соответствующую главную ось, а фазовые скорости волны, у которой векторы E и D коллинеарны соответствующей главной оси;
Главные лучевые (групповые) скорости совпадают с главными фазовыми скоростями.
Перепишем (9.19) с учетом (9.22):
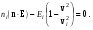 (9.23) (9.23)
Умножим обе части на ni/(1–v2/vi2) и суммируем по i. Учтем, что åniEi = nE и åni2 = 1. После приведения к общему знаменателю и деления на v2¹0 получим уравнение
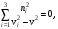 (9.24) (9.24)
которое называется уравнением Френеля. Оно позволяет найти фазовую скорость в направлении с направляющими косинусами ni. Для нахождения корней этого уравнения построим график функции (рис.9.2)
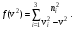 (9.25) (9.25)
Из рисунка видно, что существует только два вещественных решения уравнения Френеля (v’ и v’’), т.е. в заданном направлении могут распространяться волны с двумя различными фазовыми скоростями v’ и v’’, заключенными между наименьшей и средней, средней и наибольшей из главных скоростей (на рис.9.2 главные скорости обозначены пунктиром).
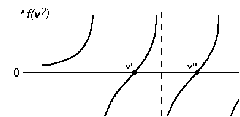 Найдем состояния поляризации в этих двух волнах. Пусть D/ и D// – векторы электрического смещения в них. Умножим (9.18) для D/ и E/ скалярно на D// и вычтем из него почленно это же соотношение для D// и E//, умноженное скалярно на D/. Тогда получим: Найдем состояния поляризации в этих двух волнах. Пусть D/ и D// – векторы электрического смещения в них. Умножим (9.18) для D/ и E/ скалярно на D// и вычтем из него почленно это же соотношение для D// и E//, умноженное скалярно на D/. Тогда получим:
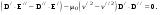 (9.26) (9.26)
Учтем, что
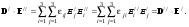 (9.27) (9.27)
Тогда, чтобы выполнялось равенство (9.26) при отличающихся значениях v’ и v’’, необходимо выполнение соотношения: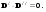 (9.28) (9.28)
Это означает, что векторы D двух волн с двумя различными скоростями v’ и v’’, которые могут распространяться в данном направлении, взаимно перпендикулярны.
Ход лучей в анизотропной среде. Исходя из определения, лучевая (групповая) скорость u и фазовая скорость v в анизотропной среде связаны соотношением:
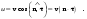 (9.29) (9.29)
Аналогично (9.24) можно вывести (вывести самостоятельно!) уравнение Френеля для лучевых скоростей:
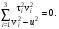 (9.30) (9.30)
Так же как и для случая фазовых скоростей, две волны (луча), распространяющихся в данном направлении с двумя лучевыми скоростями, имеют взаимно перпендикулярные направления поляризации.
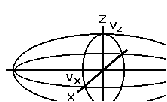 Обычно для решения одних задач по анизотропным средам удобнее работать с фазовыми скоростями, для других – с лучевыми скоростями. Произведя замену в (9.11) Обычно для решения одних задач по анизотропным средам удобнее работать с фазовыми скоростями, для других – с лучевыми скоростями. Произведя замену в (9.11) 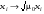 , получим уравнение: , получим уравнение:
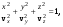 (9.31) (9.31)
где vx, vy, vz – главные лучевые скорости. Эллипсоид, точки поверхности которого удовлетворяют уравнению (9.31), называется эллипсоидом лучевых скоростей(рис.9.3) (координаты имеют размерность скоростей). Проанализируем ход лучей с помощью эллипсоида лучевых скоростей. Направление луча задается единичным вектором t. Через центр эллипсоида проведем плоскость, перпендикулярную t. В сечении эллипсоида этой плоскостью образуется эллипс с главными полуосями v1, v2 . Вектор E световой волны, распространяющейся по лучу, может колебаться только параллельно главным осям этого эллипса. Соответствующие лучевые скорости равны длинам его главных полуосей. В направлении, перпендикулярном плоскости кругового сечения, всем лучам соответствует одна и та же скорость, поляризация может быть любой. Направление, перпендикулярное круговому сечению, называется оптической осью анизотропной среды (кристалла). Для лучей, идущих вдоль оптической оси среда ведет себя как изотропная.
Эллипсоид с тремя различными полуосями (главными скоростями) имеет два круговых сечения и, отсюда, две оптические оси. Такие кристаллы называются двуосными. Если у эллипсоида лучевых скоростей любые две главные скорости совпадаю по величине, то это эллипсоид вращения. Он имеет лишь одно круговое сечение (и одну оптическую ось, совпадающую с осью симметрии). Такие кристаллы называются одноосными. В случае совпадения всех трех главных скоростей мы имеем изотропную среду. Лучи в анизотропной среде можно рассматривать и без эллипсоида лучевых скоростей непосредственно с помощью уравнения Френеля (9.30). Введем новые переменные:
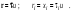 (9.32) (9.32)
В этих переменных уравнение (9.30) принимает вид:
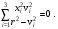 (9.33) (9.33)
Это уравнение описывает поверхность четвертого порядка, называемое лучевой поверхностью. Расстояние r от начала координат до соответствующей точки поверхности пропорциональна лучевой скорости в этом направлении t. В каждом направлении лучевая поверхность встречается два раза, что соответствует наличию двух скоростей распространения света в данном направлении.
|
 Скачать 4.65 Mb.
Скачать 4.65 Mb.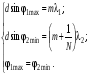 (7.66)
(7.66)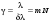 . (7.67)
. (7.67)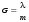 . (7.68)
. (7.68)
 амплитудой, фазой, длиной волны. Восстановленные голограммой световые волны создают полную иллюзию реальности наблюдаемых предметов.
амплитудой, фазой, длиной волны. Восстановленные голограммой световые волны создают полную иллюзию реальности наблюдаемых предметов.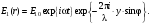 (8.1)
(8.1)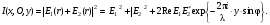 (8.2)
(8.2)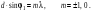 (8.3)
(8.3) Отметим, что каждый участок голограммы способен восстановить изображение всего объекта, но качество изображения при уменьшении площади голограммы ухудшается.
Отметим, что каждый участок голограммы способен восстановить изображение всего объекта, но качество изображения при уменьшении площади голограммы ухудшается. 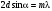 , (8.4)
, (8.4)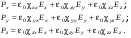 (9.1)
(9.1)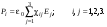 (9.2)
(9.2)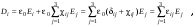 (9.3)
(9.3)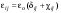 (9.4)
(9.4)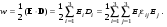 (9.5)
(9.5)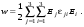 (9.6)
(9.6)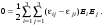 (9.7)
(9.7)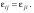 (9.8)
(9.8)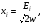 (9.9)
(9.9)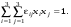 (9.10)
(9.10)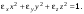 (9.11)
(9.11)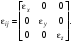 (9.12)
(9.12)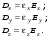 (9.13)
(9.13)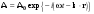 (9.14)
(9.14)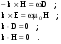 (9.15)
(9.15) вектор направления распространения волны n:
вектор направления распространения волны n: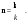 (9.16)
(9.16)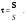 (9.17)
(9.17)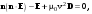 (9.18)
(9.18)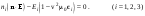 (9.19)
(9.19)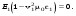 (9.20)
(9.20)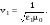 (9.21)
(9.21)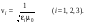 (9.22)
(9.22)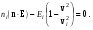 (9.23)
(9.23)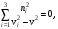 (9.24)
(9.24)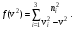 (9.25)
(9.25) Найдем состояния поляризации в этих двух волнах. Пусть D/ и D// – векторы электрического смещения в них. Умножим (9.18) для D/ и E/ скалярно на D// и вычтем из него почленно это же соотношение для D// и E//, умноженное скалярно на D/. Тогда получим:
Найдем состояния поляризации в этих двух волнах. Пусть D/ и D// – векторы электрического смещения в них. Умножим (9.18) для D/ и E/ скалярно на D// и вычтем из него почленно это же соотношение для D// и E//, умноженное скалярно на D/. Тогда получим: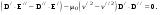 (9.26)
(9.26)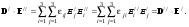 (9.27)
(9.27)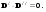 (9.28)
(9.28)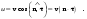 (9.29)
(9.29)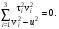 (9.30)
(9.30)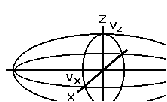 Обычно для решения одних задач по анизотропным средам удобнее работать с фазовыми скоростями, для других – с лучевыми скоростями. Произведя замену в (9.11)
Обычно для решения одних задач по анизотропным средам удобнее работать с фазовыми скоростями, для других – с лучевыми скоростями. Произведя замену в (9.11) 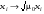 , получим уравнение:
, получим уравнение: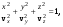 (9.31)
(9.31)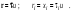 (9.32)
(9.32)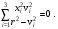 (9.33)
(9.33)