|
|
1. Оптикой
27 Многолучевая интерференция. До сих пор мы рассматривали интерференцию между двумя волнами. Теперь рассмотрим многолучевую интерференцию на примере интерферометра Фабри–Перо (ИФП) (рис.6.10). Исследуем сначала интерференцию многих световых волн при прохождении плоской монохроматической волны через плоскопараллельную диэлектрическую пластинку толщиной h и показателем преломления n. Обозначим 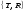 – амплитудные коэффициенты пропускания и отражения при входе волны внутрь пластины, – амплитудные коэффициенты пропускания и отражения при входе волны внутрь пластины, 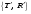 – амплитудные коэффициенты пропускания и отражения на выходе волны из пластины наружу. При этом справедливы соотношения: – амплитудные коэффициенты пропускания и отражения на выходе волны из пластины наружу. При этом справедливы соотношения:
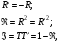 (6.34) (6.34)
где Á и Â – энергетические коэффициенты пропускания и отражения соответственно. Будем считать углы падения j и преломления q достаточно малыми, что можно считать коэффициенты отражения и пропускания независящими от этих углов. Разность хода D между соседними интерферирующими волнами на выходе пластины равна
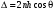 , (6.35) , (6.35)
а разность фаз равна
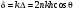 . (6.36) . (6.36)
Запаздывание последующей волны относительно предыдущей за счет прохождения волны в пластинке учтем множителем е-id. Суммарная амплитуда E2 прошедшей волны определяется суперпозицией всех прошедших пластинку волн:
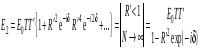 . (6.37) . (6.37)
Интенсивность света определяется следующим образом:
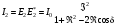 или или
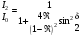 (6.38) (6.38)
Эта формула носит название формулы Эйри.
Отметим, что аналогично можно найти суммарную интенсивность света при отражении от плоскопараллельной пластинки:
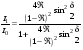 .(6.39) .(6.39)
Интерференционные картины в проходящем и отраженном свете оказываются дополнительными.
Вид функции Эйри (6.38) для трех различных коэффициентов отражения (1 – Â=0,04; 2 – Â=0,4; 3 – Â=0,8) представлен на рис.6.11. Максимумы функции 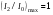 достигаются при достигаются при 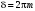 , где m = 0,1,2, ..., а минимумы , где m = 0,1,2, ..., а минимумы 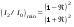 – при – при 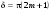 . Т.о. функция видности интерференционной картины равна: . Т.о. функция видности интерференционной картины равна:
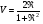 ,(6.40) ,(6.40)
 т.е. при Â ® 1 Þ V ® 1. При минимуме прошедшей проинтерферировавшей волны наблюдается максимальное отражение света от интерферометра тоже за счет интерференционного сложения волн на зеркалах. т.е. при Â ® 1 Þ V ® 1. При минимуме прошедшей проинтерферировавшей волны наблюдается максимальное отражение света от интерферометра тоже за счет интерференционного сложения волн на зеркалах.
Если на ИФП падают пучки света под всевозможными углами, то интерференционные полосы имеют вид колец. Максимальный порядок интерференции соответствует центру интерференционной картины. Интерференционная картина имеет одинаковый вид там, где падающие пучки имеют одинаковый угол падения на ИФП (полосы равного наклона). Интерференционная картина наблюдается или на бесконечности, или (что обычно реализуется в эксперименте) в фокальной плоскости линзы.
В реальных измерительных ИФП интерференция возникает между двумя отполированными с высокой точностью (
0,01l) плоскими строго параллельными (с плоскостностью до 0,005) зеркалами с большими коэффициентами отражения (алюминиевые зеркала –
75%, посеребренные –
90%, диэлектрические интерференционные – до 99,9%). Интерферометр с показателем преломления между зеркалами n = 1 называется эталоном Фабри–Перо).
28 Разрешающая способность интерферометра Фабри–Перо.
Пусть на ИФП падают две волны с близкими длинами l и l+Dl. Каждая из них создает свою интерференционную картину. При достаточно близких длинах волн возникает проблема разрешения (различения) этих двух длин волн по наложенным интерференционным картинам. Разрешающая способность интерферометра g
характеризуется минимальной разницей Dl в длинах волн, при которой возможно их разрешение:
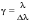 . (6.41) . (6.41)
 В теории ИФП принимается, что условием разрешения является пересечение кривых, описывающих распределение интенсивности от каждой из волн на половине их максимального значения, т.е. где В теории ИФП принимается, что условием разрешения является пересечение кривых, описывающих распределение интенсивности от каждой из волн на половине их максимального значения, т.е. где 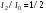 (рис.6.12). Найдем сначала ширину линии e на полувысоте из этого условия: (рис.6.12). Найдем сначала ширину линии e на полувысоте из этого условия: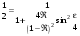 (6.42) (6.42)
При большом коэффициенте отражения e достаточно мало, так что 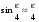 . Тогда . Тогда
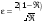 . (6.43) . (6.43)
Для эталона Фабри–Перо при достаточно больших коэффициентах отражения от пластин получаем значение разрешающей способности:
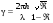 . (6.44) . (6.44)
Отсюда видно, что с увеличением Â разрешающая способность ИФП повышается. Также приводит к увеличению разрешающей способности и увеличение расстояния между пластинами h. Но добиться сколь угодно большой разрешающей способности препятствуют ряд факторов.
Факторы, ограничивающие разрешающую способность:
1. стины ИФП не могут быть сделаны абсолютно плоскими.
2. бходимо добиться параллельности пластин с той же точностью, что и для их плоскостности.
3. стояние между пластинами, умноженное на число эффективных отражений, должно быть меньше, чем длина временной когерентности исследуемого света.
Дисперсионная область. Вспомним, что разность длин волн, при которой наступает перекрытие полос соседних порядков интерференции, называется дисперсионной областью (или областью свободной дисперсии) G (см. раздел по интерференции в тонких пленках). Из определения дисперсионной области следует:
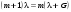 . (6.45) . (6.45)
Отсюда получаем: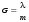 . (6.46) . (6.46)
Для ИФП при 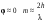 , поэтому дисперсионная область равна: , поэтому дисперсионная область равна:
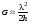 . (6.47) . (6.47)
Из сравнения формул для разрешающей способности и дисперсионной области видно, что требование повышения обеих этих величин противоречат друг другу. Для повышения разрешающей способности приходится работать на больших порядках интерференции, т.е. там, где мала дисперсионная область.
Интерференционные фильтры. Интерферометр Фабри-Перо при определенных условиях (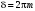 ) пропускает без ослабления световую волну с определенной длиной, а волны с длинами, лишь немного отличными от такой резонансной длины сильно ослабляются. Т.е. ИФП действует как узкополосный фильтр. Ширина полосы пропускания обычно достигает десятка ангстрем. Следует учесть, что интерференционный фильтр пропускает не только волну с заданной длиной, но и волны с длинами, смещенными на целое число дисперсионных областей, т.е. образующих следующие интерференционные максимумы (в данном случае являющиеся побочными). Поэтому, чтобы разнести побочные максимумы как можно дальше, требуется уменьшать толщину фильтра. Обычно используют оптическую толщину равную половине длины волны. Диэлектрическую пластину этой толщины покрывают с обеих сторон высокоотражающим металлическим либо диэлектрическим (см. ниже) покрытием. Для защиты от повреждений интерференционный фильтр помещают между предохранительными стеклами. ) пропускает без ослабления световую волну с определенной длиной, а волны с длинами, лишь немного отличными от такой резонансной длины сильно ослабляются. Т.е. ИФП действует как узкополосный фильтр. Ширина полосы пропускания обычно достигает десятка ангстрем. Следует учесть, что интерференционный фильтр пропускает не только волну с заданной длиной, но и волны с длинами, смещенными на целое число дисперсионных областей, т.е. образующих следующие интерференционные максимумы (в данном случае являющиеся побочными). Поэтому, чтобы разнести побочные максимумы как можно дальше, требуется уменьшать толщину фильтра. Обычно используют оптическую толщину равную половине длины волны. Диэлектрическую пластину этой толщины покрывают с обеих сторон высокоотражающим металлическим либо диэлектрическим (см. ниже) покрытием. Для защиты от повреждений интерференционный фильтр помещают между предохранительными стеклами.
Сканирующий интерферометр Фабри–Перо. Формула Эйри объясняет принцип действия широко используемого в оптике и 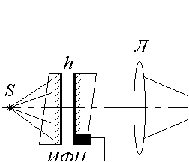 лазерной технике спектрального прибора – сканирующего интерферометра Фабри–Перо. Это своеобразный аналог измерителей частотных характеристик электрических сигналов радиодиапазона, основанных на принципе сканирования резонансной частоты колебательной системы – колебательного контура, коаксиального, полоскового или объемного резонатора. Заметим, что разность фаз линейно зависит от расстояния между пластинами. Если зафиксировать угол j, то это соответствует помещению некоторого фотоприемника в любую точку экрана (рис.6.13), где видна интерференционная картина. Оптимальное место для этого – центр картины (точка А), т.к. частотная дисперсия лазерной технике спектрального прибора – сканирующего интерферометра Фабри–Перо. Это своеобразный аналог измерителей частотных характеристик электрических сигналов радиодиапазона, основанных на принципе сканирования резонансной частоты колебательной системы – колебательного контура, коаксиального, полоскового или объемного резонатора. Заметим, что разность фаз линейно зависит от расстояния между пластинами. Если зафиксировать угол j, то это соответствует помещению некоторого фотоприемника в любую точку экрана (рис.6.13), где видна интерференционная картина. Оптимальное место для этого – центр картины (точка А), т.к. частотная дисперсия 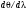 в этой точке максимальна. Поэтому конечность размеров фотоприемника минимально ухудшает разрешение ИФП как раз при таком местоположении. Теперь допустим, что одна из пластин ИФП параллельно перемещается вдоль оптической оси системы с постоянной скоростью v, т.е. h=h0+vt. Тогда пропускание ИФП становится зависимым от времени, повторяя зависимость функции Эйри. Если на ИФП падает монохроматическая волна, то на осциллографе, развертка которого движется синхронно с пластиной, сигнал от ИФП опишет его аппаратную функцию в соответствии с (6.38). При сложном спектре электрический сигнал опишет исследуемый спектр. На практике перемещение пластин осуществляется или изменением давления газа между пластинами ИФП, или креплением одной из пластин на пьезокерамику. Второй способ предпочтительней, т.к. позволяет осуществить сканирование величины в этой точке максимальна. Поэтому конечность размеров фотоприемника минимально ухудшает разрешение ИФП как раз при таком местоположении. Теперь допустим, что одна из пластин ИФП параллельно перемещается вдоль оптической оси системы с постоянной скоростью v, т.е. h=h0+vt. Тогда пропускание ИФП становится зависимым от времени, повторяя зависимость функции Эйри. Если на ИФП падает монохроматическая волна, то на осциллографе, развертка которого движется синхронно с пластиной, сигнал от ИФП опишет его аппаратную функцию в соответствии с (6.38). При сложном спектре электрический сигнал опишет исследуемый спектр. На практике перемещение пластин осуществляется или изменением давления газа между пластинами ИФП, или креплением одной из пластин на пьезокерамику. Второй способ предпочтительней, т.к. позволяет осуществить сканирование величины 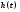 электрическим сигналом. электрическим сигналом.
Принцип Фурье-спектроскопии. Пусть излучение немонохроматично и обладает непрерывным спектром. В интервале волновых чисел от k до k+dk интенсивность определяется спектром F(k) и интервалом dk :
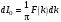 . (6.48) . (6.48)
В результате интерференции с учетом разности хода D имеем:
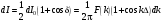 .(6.49) .(6.49)
Полная интенсивность определяется интегралом:
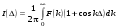 (6.50) (6.50)
Это равенство при D=0 примет вид:
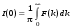 . (6.51) . (6.51)
Тогда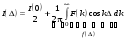 (6.52) (6.52)
Второе слагаемое в (6.52) f(D) называется интерферограммой. Обратное преобразование Фурье имеет вид:
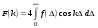 . (6.53) . (6.53)
Подставив интенсивность интерферограммы в виде функции разности хода лучей D и вычислив f(D), с помощью (6.53) получаем спектральный состав излучения. Такой метод определения спектров называется Фурье-спектроскопией. Рассмотрим еще некоторые применения интерференционных явлений в современной 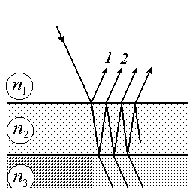 технике. Просветление оптики. Во многих современных оптических системах используются многочисленные оптические детали (линзы, призмы и др.), отражение от которых ослабляют интенсивность прошедшего света. Поэтому сведение к минимуму френелевских (т.е. рассчитываемых по формулам Френеля) потерь (просветление оптики) становится важной задачей. Явление интерференции позволяет сделать это достаточно эффективно. Для этого на поверхность оптического элемента наносят тонкий слой вещества (пленку), в которой и происходит интерференция (рис.6.14). Пусть n1 – коэффициент преломления внешней среды, из которой падает свет, n2 , h – соответственно коэффициент преломления и оптическая толщина пленки, n3 – коэффициент преломления оптического элемента. Если рассмотреть только двухлучевую интерференцию между волнами 1 и 2, то для полного гашения отраженных пучков, т.е. для полного просветления оптики, необходимо выполнение двух условий: технике. Просветление оптики. Во многих современных оптических системах используются многочисленные оптические детали (линзы, призмы и др.), отражение от которых ослабляют интенсивность прошедшего света. Поэтому сведение к минимуму френелевских (т.е. рассчитываемых по формулам Френеля) потерь (просветление оптики) становится важной задачей. Явление интерференции позволяет сделать это достаточно эффективно. Для этого на поверхность оптического элемента наносят тонкий слой вещества (пленку), в которой и происходит интерференция (рис.6.14). Пусть n1 – коэффициент преломления внешней среды, из которой падает свет, n2 , h – соответственно коэффициент преломления и оптическая толщина пленки, n3 – коэффициент преломления оптического элемента. Если рассмотреть только двухлучевую интерференцию между волнами 1 и 2, то для полного гашения отраженных пучков, т.е. для полного просветления оптики, необходимо выполнение двух условий:
1) плитуды пучков должны быть равными;
2) разность фаз между ними должна равняться p (т.е. волны находятся в противофазе).
Первое условие достигается подбором показателя преломления пленки. Второе условие легко выполняется, если оптическая толщина пленки равна l/4.
Более точно и правильнее соотношение для показателя преломления пленки можно найти, рассмотрев аналогично интерферометру Фабри–Перо многолучевую интерференцию. Тогда для относительной интенсивности отраженного от такой системы света получаем (проверить самостоятельно):
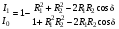 , (6.54) , (6.54)
где 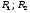 – амплитудные коэффициенты отражения от первой и второй границ раздела соответственно, d – оптическая разность хода между двумя соседними интерферирующими волнами. Положив d=p, а падение – нормальным, получаем: – амплитудные коэффициенты отражения от первой и второй границ раздела соответственно, d – оптическая разность хода между двумя соседними интерферирующими волнами. Положив d=p, а падение – нормальным, получаем: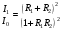 . (6.55) . (6.55)
Т.к. при нормальном падении света 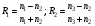 , то интенсивность отраженного света будет равна нулю, если , то интенсивность отраженного света будет равна нулю, если
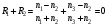 . (6.56) . (6.56)
Тогда окончательно получаем условие полного просветления (совместно с 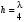 : :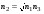 . (6.57) . (6.57)
Если первая среда – воздух, а третья – стекло, то удовлетворить этому соотношению весьма трудно, т.к. твердых веществ со столь малым коэффициентом преломления (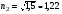 ) в оптическом преломления не существует. Существующие вещества типа виллиолента (NaF), криолита (Na3AlF6) (показатели преломления ) в оптическом преломления не существует. Существующие вещества типа виллиолента (NaF), криолита (Na3AlF6) (показатели преломления 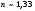 ) позволяют уменьшить коэффициент отражения до 0,8%. Дальнейшее уменьшение коэффициента отражения может быть достигнуто применением многослойных просветляющих покрытий. Высокоотражающие интерференционные покрытия (интерференционные зеркала). Кроме просветления оптики часто необходимо решить противоположную задачу – увеличить коэффициент отражения от поверхности. Это необходимо, например, при создании лазерных интерференционных зеркал с заданным коэффициентом отражения. Рассматривая систему, аналогичную полученной для просветления оптики, легко убедиться, что если взять показатель преломления диэлектрического слоя больше показателя преломления подложки, а оптическая толщина слоя остается равной l/4, то произойдет увеличение коэффициента отражения вследствие взаимного усиления отраженных волн. Но за счет нанесения одного слоя добиться коэффициента отражения больше 30% не удается. Обычно используют многолучевую интерференцию за счет нанесения системы чередующихся слоев с большим и малым показателями преломления. Обычно используют комбинацию сульфида цинка (n = 2,3) и фторида лития (n = 1,3). Для получения коэффициента отражения 99% надо нанести 11 – 13 слоев. ) позволяют уменьшить коэффициент отражения до 0,8%. Дальнейшее уменьшение коэффициента отражения может быть достигнуто применением многослойных просветляющих покрытий. Высокоотражающие интерференционные покрытия (интерференционные зеркала). Кроме просветления оптики часто необходимо решить противоположную задачу – увеличить коэффициент отражения от поверхности. Это необходимо, например, при создании лазерных интерференционных зеркал с заданным коэффициентом отражения. Рассматривая систему, аналогичную полученной для просветления оптики, легко убедиться, что если взять показатель преломления диэлектрического слоя больше показателя преломления подложки, а оптическая толщина слоя остается равной l/4, то произойдет увеличение коэффициента отражения вследствие взаимного усиления отраженных волн. Но за счет нанесения одного слоя добиться коэффициента отражения больше 30% не удается. Обычно используют многолучевую интерференцию за счет нанесения системы чередующихся слоев с большим и малым показателями преломления. Обычно используют комбинацию сульфида цинка (n = 2,3) и фторида лития (n = 1,3). Для получения коэффициента отражения 99% надо нанести 11 – 13 слоев.
 30 Зоны Френеля. Пусть сферическая волна падает на непрозрачный экран с отверстием. Требуется найти распределение интенсивности света за экраном. Для решения этой задачи делаются два предположения: 30 Зоны Френеля. Пусть сферическая волна падает на непрозрачный экран с отверстием. Требуется найти распределение интенсивности света за экраном. Для решения этой задачи делаются два предположения:
непроницаемые части экрана не являются источниками вторичных волн;
в отверстии точки волнового фронта являются такими же источниками вторичных волн, какими они были бы при отсутствии непроницаемых частей экрана.
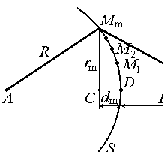
Пусть A – источник сферической волны, S – волновой фронт в некоторый момент времени, R – радиус кривизны этого фронта (рис.7.2). Найдем интенсивность в точке P с помощью принципа Гюйгенса – Френеля. Разобьем поверхность S на кольцеобразные зоны такого размера, чтобы расстояния от краев зоны (в разрезе это соответствует точкам M1, M2, M3 , …) до P отличались на l/2 (эти зоны называются зонами Френеля):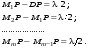 (7.3) (7.3)
Из геометрии рис.7.3 можно получить для радиуса m–й зоны Френеля rm :
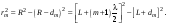 (7.4) (7.4)
Исключая величину dm и пренебрегая слагаемыми
l2 ввиду их малости, получаем:
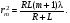 (7.5) (7.5)
Площади всех зон Френеля примерно одинаковы (в случае пренебрежения кривизной поверхности, что не вносит существенной ошибки, если радиусы зон Френеля много меньше радиуса кривизны волнового фронта (обычно это справедливо для очень большого числа зон Френеля)):
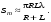 (7.6) (7.6)
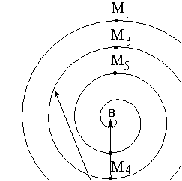 Графическое вычисление амплитуды (метод векторных диаграмм). Разделим каждую из зон на большое число N участков. Между началом и концом зоны фаза меняется на p, а между малыми участками – на d = p/N . Пусть E0 – амплитуда волны, приходящей в точку наблюдения P от каждого участка; а фаза волны, приходящей из точки D в точку P – равна нулю. Комплексная амплитуда волны в точке P от центральной зоны Френеля с учетом интерференции равна: Графическое вычисление амплитуды (метод векторных диаграмм). Разделим каждую из зон на большое число N участков. Между началом и концом зоны фаза меняется на p, а между малыми участками – на d = p/N . Пусть E0 – амплитуда волны, приходящей в точку наблюдения P от каждого участка; а фаза волны, приходящей из точки D в точку P – равна нулю. Комплексная амплитуда волны в точке P от центральной зоны Френеля с учетом интерференции равна:
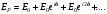 (7.7) (7.7)
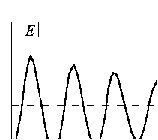
Аналитическое сложение амплитуд можно проделать графически, изображая комплексную амплитуду в виде вектора (рис.7.3). При увеличении числа разбиений до бесконечности ломаная кривая превращается в плавную. Длина вектора DM1 пропорциональна амплитуде волны в точке P, когда открыта вся центральная зона Френеля. Аналогично продолжая построение, можно получить кривую, по которой легко определить амплитуду волны (и ее интенсивность), зная соотношение диаметров открываемого отверстия и зон Френеля. При строгом равенстве амплитуд в (7.7) складываемых колебаний от элементарных участков результирующая амплитуда от двух открытых соседних зон была бы равна нулю, т.е. вторичные волны в результате интерференции гаси ли бы друг друга, но коэффициент наклона K(a) в (7.1) убывает по мере увеличения a и приводит к уменьшению амплитуд вторичных волн. Поэтому полученная кривая не замыкается, а имеет вид спирали. Зависимость амплитуды поля в точке P от радиуса отверстия показана на рис.7.4.
 Пятно Пуассона. Если на пути световой волны стоит непрозрачный круглый экран, то за экраном в его тени на оси возникает светлое пятно, называемое пятном Пуассона. Необходимость возникновения светлого пятна очевидна из рассуждений по методу зон Френеля. Экран закрывает некоторое число зон Френеля начиная с центральной. Однако следующие зоны после последней из закрытых создают в точке P освещенность, значение которой можно рассчитать с помощью спирали. Т.о., получается, что волна как бы огибает непрозрачный экран. Интенсивность пятна Пуассона весьма слаба при больших размерах непрозрачного экрана. Кроме того, необходимо, чтобы свет обладал достаточно большой степенью когерентности. Пятно Пуассона. Если на пути световой волны стоит непрозрачный круглый экран, то за экраном в его тени на оси возникает светлое пятно, называемое пятном Пуассона. Необходимость возникновения светлого пятна очевидна из рассуждений по методу зон Френеля. Экран закрывает некоторое число зон Френеля начиная с центральной. Однако следующие зоны после последней из закрытых создают в точке P освещенность, значение которой можно рассчитать с помощью спирали. Т.о., получается, что волна как бы огибает непрозрачный экран. Интенсивность пятна Пуассона весьма слаба при больших размерах непрозрачного экрана. Кроме того, необходимо, чтобы свет обладал достаточно большой степенью когерентности.
Отметим, что можно наблюдать и противоположный эффект – темное пятно в центре картинки при дифракции на открытом отверстии. Такое пятно называется пятном Араго.
|
|
|
 Скачать 4.65 Mb.
Скачать 4.65 Mb.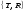 – амплитудные коэффициенты пропускания и отражения при входе волны внутрь пластины,
– амплитудные коэффициенты пропускания и отражения при входе волны внутрь пластины, 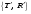 – амплитудные коэффициенты пропускания и отражения на выходе волны из пластины наружу. При этом справедливы соотношения:
– амплитудные коэффициенты пропускания и отражения на выходе волны из пластины наружу. При этом справедливы соотношения: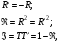 (6.34)
(6.34)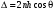 , (6.35)
, (6.35)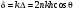 . (6.36)
. (6.36)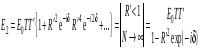 . (6.37)
. (6.37)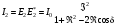 или
или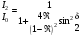 (6.38)
(6.38)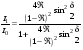 .(6.39)
.(6.39)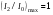 достигаются при
достигаются при 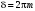 , где m = 0,1,2, ..., а минимумы
, где m = 0,1,2, ..., а минимумы 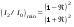 – при
– при 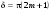 . Т.о. функция видности интерференционной картины равна:
. Т.о. функция видности интерференционной картины равна: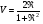 ,(6.40)
,(6.40)
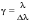 . (6.41)
. (6.41)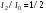 (рис.6.12). Найдем сначала ширину линии e на полувысоте из этого условия:
(рис.6.12). Найдем сначала ширину линии e на полувысоте из этого условия: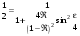 (6.42)
(6.42)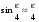 . Тогда
. Тогда 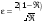 . (6.43)
. (6.43)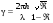 . (6.44)
. (6.44)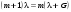 . (6.45)
. (6.45)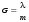 . (6.46)
. (6.46)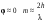 , поэтому дисперсионная область равна:
, поэтому дисперсионная область равна: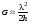 . (6.47)
. (6.47) лазерной технике спектрального прибора – сканирующего интерферометра Фабри–Перо. Это своеобразный аналог измерителей частотных характеристик электрических сигналов радиодиапазона, основанных на принципе сканирования резонансной частоты колебательной системы – колебательного контура, коаксиального, полоскового или объемного резонатора. Заметим, что разность фаз линейно зависит от расстояния между пластинами. Если зафиксировать угол j, то это соответствует помещению некоторого фотоприемника в любую точку экрана (рис.6.13), где видна интерференционная картина. Оптимальное место для этого – центр картины (точка А), т.к. частотная дисперсия
лазерной технике спектрального прибора – сканирующего интерферометра Фабри–Перо. Это своеобразный аналог измерителей частотных характеристик электрических сигналов радиодиапазона, основанных на принципе сканирования резонансной частоты колебательной системы – колебательного контура, коаксиального, полоскового или объемного резонатора. Заметим, что разность фаз линейно зависит от расстояния между пластинами. Если зафиксировать угол j, то это соответствует помещению некоторого фотоприемника в любую точку экрана (рис.6.13), где видна интерференционная картина. Оптимальное место для этого – центр картины (точка А), т.к. частотная дисперсия 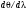 в этой точке максимальна. Поэтому конечность размеров фотоприемника минимально ухудшает разрешение ИФП как раз при таком местоположении. Теперь допустим, что одна из пластин ИФП параллельно перемещается вдоль оптической оси системы с постоянной скоростью v, т.е. h=h0+vt. Тогда пропускание ИФП становится зависимым от времени, повторяя зависимость функции Эйри. Если на ИФП падает монохроматическая волна, то на осциллографе, развертка которого движется синхронно с пластиной, сигнал от ИФП опишет его аппаратную функцию в соответствии с (6.38). При сложном спектре электрический сигнал опишет исследуемый спектр. На практике перемещение пластин осуществляется или изменением давления газа между пластинами ИФП, или креплением одной из пластин на пьезокерамику. Второй способ предпочтительней, т.к. позволяет осуществить сканирование величины
в этой точке максимальна. Поэтому конечность размеров фотоприемника минимально ухудшает разрешение ИФП как раз при таком местоположении. Теперь допустим, что одна из пластин ИФП параллельно перемещается вдоль оптической оси системы с постоянной скоростью v, т.е. h=h0+vt. Тогда пропускание ИФП становится зависимым от времени, повторяя зависимость функции Эйри. Если на ИФП падает монохроматическая волна, то на осциллографе, развертка которого движется синхронно с пластиной, сигнал от ИФП опишет его аппаратную функцию в соответствии с (6.38). При сложном спектре электрический сигнал опишет исследуемый спектр. На практике перемещение пластин осуществляется или изменением давления газа между пластинами ИФП, или креплением одной из пластин на пьезокерамику. Второй способ предпочтительней, т.к. позволяет осуществить сканирование величины 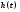 электрическим сигналом.
электрическим сигналом.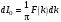 . (6.48)
. (6.48)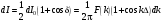 .(6.49)
.(6.49)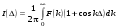 (6.50)
(6.50)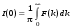 . (6.51)
. (6.51)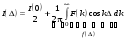 (6.52)
(6.52)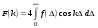 . (6.53)
. (6.53) технике. Просветление оптики. Во многих современных оптических системах используются многочисленные оптические детали (линзы, призмы и др.), отражение от которых ослабляют интенсивность прошедшего света. Поэтому сведение к минимуму френелевских (т.е. рассчитываемых по формулам Френеля) потерь (просветление оптики) становится важной задачей. Явление интерференции позволяет сделать это достаточно эффективно. Для этого на поверхность оптического элемента наносят тонкий слой вещества (пленку), в которой и происходит интерференция (рис.6.14). Пусть n1 – коэффициент преломления внешней среды, из которой падает свет, n2 , h – соответственно коэффициент преломления и оптическая толщина пленки, n3 – коэффициент преломления оптического элемента. Если рассмотреть только двухлучевую интерференцию между волнами 1 и 2, то для полного гашения отраженных пучков, т.е. для полного просветления оптики, необходимо выполнение двух условий:
технике. Просветление оптики. Во многих современных оптических системах используются многочисленные оптические детали (линзы, призмы и др.), отражение от которых ослабляют интенсивность прошедшего света. Поэтому сведение к минимуму френелевских (т.е. рассчитываемых по формулам Френеля) потерь (просветление оптики) становится важной задачей. Явление интерференции позволяет сделать это достаточно эффективно. Для этого на поверхность оптического элемента наносят тонкий слой вещества (пленку), в которой и происходит интерференция (рис.6.14). Пусть n1 – коэффициент преломления внешней среды, из которой падает свет, n2 , h – соответственно коэффициент преломления и оптическая толщина пленки, n3 – коэффициент преломления оптического элемента. Если рассмотреть только двухлучевую интерференцию между волнами 1 и 2, то для полного гашения отраженных пучков, т.е. для полного просветления оптики, необходимо выполнение двух условий: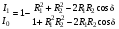 , (6.54)
, (6.54)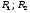 – амплитудные коэффициенты отражения от первой и второй границ раздела соответственно, d – оптическая разность хода между двумя соседними интерферирующими волнами. Положив d=p, а падение – нормальным, получаем:
– амплитудные коэффициенты отражения от первой и второй границ раздела соответственно, d – оптическая разность хода между двумя соседними интерферирующими волнами. Положив d=p, а падение – нормальным, получаем: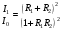 . (6.55)
. (6.55)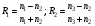 , то интенсивность отраженного света будет равна нулю, если
, то интенсивность отраженного света будет равна нулю, если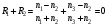 . (6.56)
. (6.56)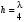 :
: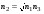 . (6.57)
. (6.57)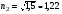 ) в оптическом преломления не существует. Существующие вещества типа виллиолента (NaF), криолита (Na3AlF6) (показатели преломления
) в оптическом преломления не существует. Существующие вещества типа виллиолента (NaF), криолита (Na3AlF6) (показатели преломления 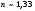 ) позволяют уменьшить коэффициент отражения до 0,8%. Дальнейшее уменьшение коэффициента отражения может быть достигнуто применением многослойных просветляющих покрытий.
) позволяют уменьшить коэффициент отражения до 0,8%. Дальнейшее уменьшение коэффициента отражения может быть достигнуто применением многослойных просветляющих покрытий.  30 Зоны Френеля. Пусть сферическая волна падает на непрозрачный экран с отверстием. Требуется найти распределение интенсивности света за экраном. Для решения этой задачи делаются два предположения:
30 Зоны Френеля. Пусть сферическая волна падает на непрозрачный экран с отверстием. Требуется найти распределение интенсивности света за экраном. Для решения этой задачи делаются два предположения: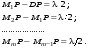 (7.3)
(7.3)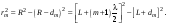 (7.4)
(7.4)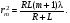 (7.5)
(7.5)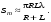 (7.6)
(7.6)
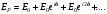 (7.7)
(7.7) Пятно Пуассона. Если на пути световой волны стоит непрозрачный круглый экран, то за экраном в его
Пятно Пуассона. Если на пути световой волны стоит непрозрачный круглый экран, то за экраном в его